반응표면법을 이용한 축류 압축기의 동익형상 최적설계

1. 서 론

축류 압축기는 가스터빈, 스팀터빈과 같은 발전설비, 항공기의 추진기관 등 산업 전 분야에서 사용되고 있으며, 특히 가스터빈을 이용하는 항공용 엔진부분과 발전설비 부분에서 주요 구성품으로 사용되고 있다⁽¹⁾. 천음속 축류 압축기의 내부 유동장은 동익 형상에 의해 발생되는 이차유동, 와류, 경계층박리, 후류, 충격파 등으로 인해 매우 복잡한 3차원 유동구조를 갖고 있으며, 특히 충격파/경계층의 상호작용에 의해 발생되는 현상은 내부 유동에서 중요한 현상으로 알려져 있다^(2-4). 따라서 충격파의 발생 위치와 강도 뿐만 아니라, 이로 인해 발생하는 박리현상의 위치 등은 공력학적 성능을 예측하는데 필수적으로 해석되어야 하는 요소들이고, Navier-Stokes 해법은 이러한 현상들을 정확히 예측하기 위한 좋은 방법으로 제시되고 있다^(4-6). 컴퓨터의 성능향상과 더불어, 수치최적화 설계기법에 의한 동익의 설계 연구가 10 여년 전부터 활발히 진행되고 있다^(7-8). Marz 등⁽⁹⁾은 아음속, 천음속 압축기에 대한 유동장 시험과 수치해석을 수행하여 내부 유동장을 상호 비교하였으며, Hah⁽¹⁰⁾는 블레이드에 대해 수치해석을 수행하여 천음속 축류 압축기에 있어서 난류모델이 수치해석 결과에 미치는 영향을 연구하였다. 또한, Jang 등⁽⁴⁾은 반응면 기법을 이용하여 천음속 축류 압축기 동익의 스윕각을 최적설계 하였으며, Ahn과 Kim⁽¹¹⁾은 stacking line을 반경방향으로 경사지도록 하는 요소들을 이용하여 동익의 3차원적 형상을 최적화 하였다.

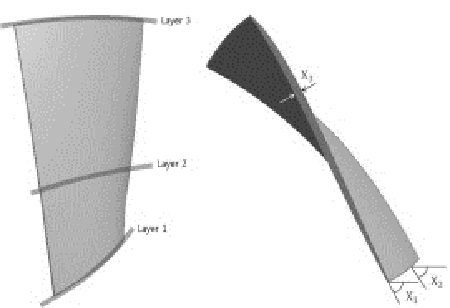
본 연구에서는 실험계획법과 반응표면법을 이용하여 천음속 축류 압축기의 동익 형상에 대해서 최적설계를 수행하였다. 설계변수로는 전연(leading edge, LE)에서의 각도와 두께를 선택하여 기본모델보다 높은 성능을 갖는 블레이드에 대한 3차원적 최적형상을 도출하였다.

2. 수치해석

2.1 기본모델

본 연구에 사용된 기본모델은 NASA rotor 37을 갖는 단단 축류 압축기이며, 3차원 모델과 설계변수를 Fig. 1에 나타내었다. 이 동익은 Reid 등⁽⁵⁾에 의해서 설계되고 실험되었으며, 36개의 블레이드로 구성되어있다. 3차원 형상은 ANSYS Blade editor를 이용하여 설계하였으며, 동익 형상 최적화를 위해 선정된 기본적인 변수들에 대한 변수화를 Table 1에 나타내었다. 해석에 사용된 축류 압축기의 작동유체는 공기이며, 출구 유량은 20.19 kg/s, 회전속도는 약 17189 rpm이다.

Fig. 1

Reference model and description of design parameter

Table 1

Design parameters of the modeled compressor

2.2 격자계 구성 및 경계조건

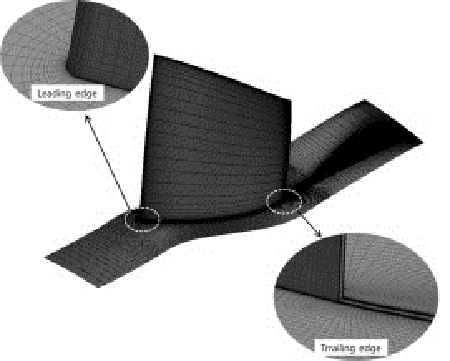
수치해석에 사용된 격자계는 ANSYS Turbogrid를 사용하였으며, 익형 주변을 제외한 영역에는 H-형 격자를 사용하였다. 격자의 개수는 1,000,000개로 설정하였으며, 격자계를 Fig. 2에 나타내었다.

Fig. 2

Grid systems

수치해석은 ANSYS CFX 16.0을 이용하여 해석영역을 동익 입구에서부터 출구까지 설정하였으며, 작동유체는 이상기체를 사용하여 정상상태 해석을 수행하였다. 지배방정식으로는 3차원 Navier-Stokes 방정식과 에너지 방정식이 사용되었으며, 난류모델로는 SST(shear stress transport)를 사용하였다. 입구 경계면에서는 전온도, 전압력을 지정하였고, 출구 경계면에서는 질량유량을 조건으로 지정하였다. 경계조건은 Table 2에 나타내었다.

Table 2

Boundary conditions applied in this study

축류 압축기의 동익 형상 최적화를 하기 위해 단단 압축기에 주로 사용되는 단열효율, 압력비, 압력손실계수를 사용하여 성능을 평가하였다. 온도 상승이 크지 않을 경우, 일정한 압력에 대한 비열이 입구부와 출구부에서 거의 일정하므로, 단열효율을 목적함수로 사용하였고⁽¹²⁾, 압축기 성능을 평가하기 위하여 압력비와 전압력 손실계수를 사용하였다.

$\[ \mathrm{A}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{ }\mathrm{E}\mathrm{f}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{y},\eta =\frac{{\left({\mathrm{P}}_{0\mathrm{e}\mathrm{x}\mathrm{i}\mathrm{t}}/{\mathrm{P}}_{0\mathrm{i}\mathrm{n}\mathrm{l}\mathrm{e}\mathrm{t}}\right)}^{\frac{\gamma -1}{\gamma }}}{{\mathrm{T}}_{0\mathrm{e}\mathrm{x}\mathrm{i}\mathrm{t}}/{\mathrm{T}}_{0\mathrm{i}\mathrm{n}\mathrm{l}\mathrm{e}\mathrm{t}}} \]$

(1)

$\[ \mathrm{Pressure\; ratio},{\mathrm{P}}_{\mathrm{R}}=\frac{\mathrm{outlet\; pressure}}{\mathrm{inlet\; pressure}} \]$

(2)

$\[ \mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{ }\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{ }\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}\mathrm{ }\mathrm{c}\mathrm{o}\mathrm{e}\mathrm{f}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{t},\mathrm{K}=\frac{{\mathrm{P}}_{0\mathrm{e}\mathrm{x}\mathrm{i}\mathrm{t}}/{\mathrm{P}}_{0\mathrm{i}\mathrm{n}\mathrm{l}\mathrm{e}\mathrm{t}}}{\frac{1}{2}\rho {\mathrm{U}}^2} \]$

(3)

여기서 P₀와 T₀는 각각 전압과 전온도를 의미하며, 하첨자 inlet과 exit은 단단 축류 압축기의 입구부와 출구부를 각각 의미한다.

3. 최적설계

3.1 실험계획법

최적설계를 수행하는데 있어서 최적 값에 수렴할 때까지 반복되는 계산은 수백 번 이상이 필요하다. 모든 과정마다 수치해석을 수행하게 되면 상당히 많은 계산 시간이 소요되기 때문에 설계변수와 목적함수 사이의 근사모델을 구성하여 최적설계를 수행하는 것이 효율적이다⁽¹³⁾. 본 연구에서는 전산수치 실험에서 많이 사용되고 있는 중심합성계획법(central composite design, CCD)을 사용하였다. 중심합성계획은 다음 식과 같이 구성되어 있다.

$\[ \mathrm{y}=2^{\mathrm{k}}+2\mathrm{k}+1 \]$

(4)

여기서 y는 실험의 개수, k는 설계변수의 수 이다. 설계변수의 수는 3개이므로 총 15개의 실험개수가 도출되며, 실험값과 수치해석의 결과를 Table 3에 나타내었다.

Table 3

Parameters of DOE

4. 결과 및 고찰

4.1 기본 모델

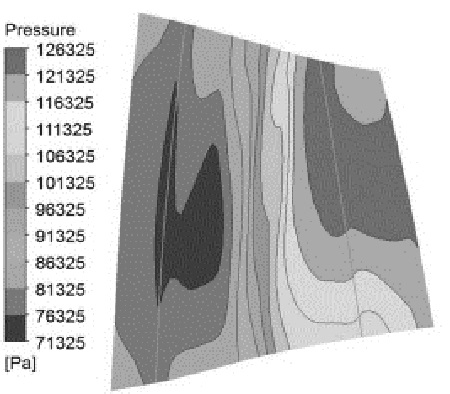
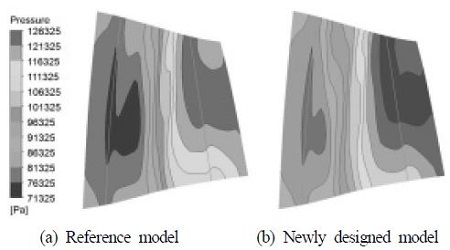
먼저, 축류 압축기 성능변수를 계산하였는데, 단열 효율은 86.61%, 압력비는 1.80, 압력손실계수는 0.42959를 얻었다. Fig. 3에 자오면에서의 압력분포를 나타내었다. 동익의 입구에서부터 출구까지 압력이 상승하는 것을 확인할 수 있다.

Fig. 3

Meridional view of pressure distribution

4.2 민감도 분석

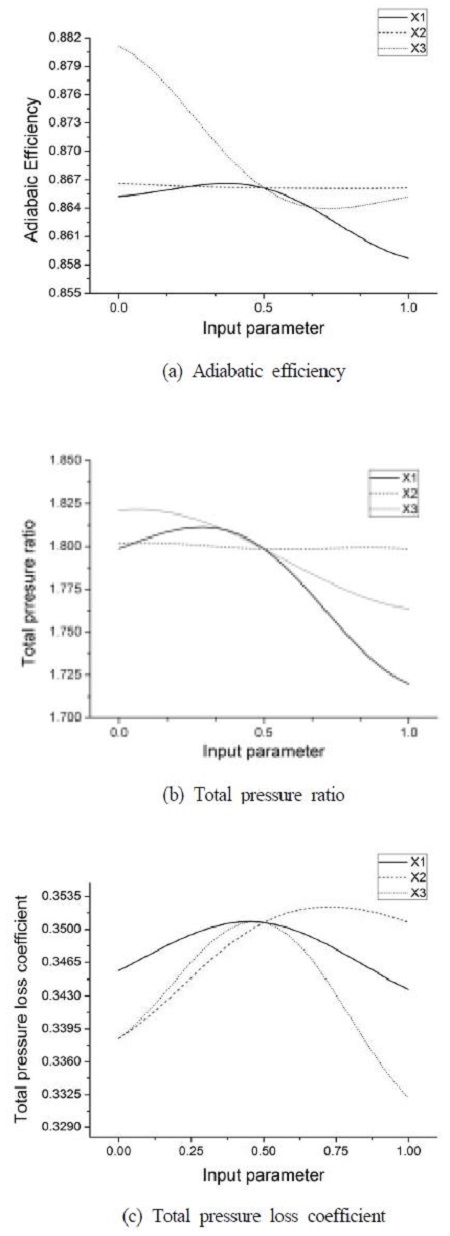
Fig. 4은 NPR방법의 설계변수 변화에 따른 응답변수의 민감도를 나타낸다. X축은 입력변수로 그 범위를 0에서 1까지 무차원화 하였으며, 기본모델의 설계변수 값은 0.5를 의미한다. 첫 번째, 단열효율에 대한 응답표면 결과를 보면, X₁는 출력변수와 음의 관계를 보이며 입력변수 값이 0 부근에서 최대값을 나타내었다. 변수 X₂, X₃ 또한 출력변수와 음의 관계를 보이지만, X₁에 비하여 상대적으로 낮은 효과를 보였다. 두 번째 압력손실계수에 관한 응답표면 결과에서 X₁, X₃는 입력변수 0.0∼0.5 구간에서는 양의 관계, 0.5∼1.0 구간에서는 음의관계를 보이는 것을 알 수 있다. 또한, X₂는 출력변수와 양의 관계를 보이며 입력변수 값이 0.7 부근에서 최대값을 나타내었다. 마지막으로, 압력비에 관한 응답표면 결과에서는 X₁과 X₃가 출력변수에 음의 관계를 보였으며, X₂가 미치는 영향은 상대적으로 낮았다. 이 결과를 통해 단열효율, 압력비에서 음의 관계를 갖는 변수와 압력손실계수에서 양의 관계를 갖는 변수들은 축류 압축기의 공력성능에 긍정적인 영향을 미치는 중요한 설계 변수임을 알 수 있다.

Fig. 4

Results of sensitivity with various design parameters

4.3 최적화 결과

반응표면법과 수치해석의 최적화 결과를 Table 4에 나타내었다. 반응표면법을 통한 단열효율에 대한 근사모델과 CFD 결과의 상대오차는 0.3% 발생하였고, 압력손실계수는 0.4%, 압력비는 0.07%의 차이를 보였다. 모든 출력변수가 모두 근사모델과 높은 적합도를 보였으며, 압력비는 가장 정확히 예측되었다. 결과적으로 단열 효율과 압력비의 근사모델 적합도는 아주 높다는 것을 유추할 수 있다.

Table 4

Comparison results between RSM and CFD analyses

Table 5에 기본모델과 최적모델의 결과를 비교하였다. 최적설계 결과로 목적함수이자 축류 압축기의 주요 성능 변수인 단열효율은 약 1.47% 증가하였다. 제한조건인 압력손실계수는 5.2% 감소하였으며, 압력비는 1.2% 증가하였다.

Table 5

Comparison results between Ref. model and newly designed model

Fig. 5에 동익 자오면에서의 압력상승 분포를 나타내었다. 최적모델이 기본모델에 비해 높은 압력상승 분포를 나타내고 있는데, 이는 최적화를 통한 결과임을 알 수 있다.

Fig. 5

Pressure distributions at the rotor meridional plane

5. 결 론

본 연구에서는 축류 압축기 동익에 대한 형상을 3차원적으로 최적화 하였다. 최적 설계 과정에서 실험계획법과 반응표면법의 사용으로 다수의 설계변수와 성능 간의 상관관계를 분석하여 축류 압축기의 주요한 설계변수를 선정하였다.

형상 최적설계의 결과로 최적 모델은 초기모델보다 압력비 1.2% 증가, 압력손실계수 5.2% 감소하였으며, 단열효율은 1.47% 증가하는 동익 형상을 도출하였다.

Acknowledgments

본 연구는 국토교통부 플랜트연구개발사업의 연구비지원(15IFIP-B089065-02)에 의해 수행되었습니다.

References

• Park, T. C., Kang, Y. S., Hwang, O. S., Song, J. H., and Lim, B. J., (2012), “Design Optimization of a Single-Stage Transonic Axial Compressor and Test Evaluation of Its Aerodynamic Performance”, The KSFM Journal of Fluid Machinery, 15(6), p77-84. [https://doi.org/10.5293/kfma.2012.15.6.077]
• Suder, K. L., and Celestina, M. L., (1994), “Experimental and Computational Investigation of the Tip Clearance Flow in a Transonic Axial Compressor Rotor”, ASME paper 94-GT-365.
• Hah, C., and Loellbach, J., (1999), “Development of Hub Corner Stall and Its Influence on the Performance of Axial Compressor Blade Rows”, ASME Journal of Turbomachin, 121(1), p67-77. [https://doi.org/10.1115/1.2841235]
• Jang, C. M., Li, P., and Kim, K. Y., (2006), “Optimization of Blade Sweep of NASA Rotor 37”, Transaction of the KSME B, 30(7), p622-629. [https://doi.org/10.3795/ksme-b.2006.30.7.622]
• Chima, R. V., (1998), “Calculation of Tip Clearance Effects in a Transonic Compressor Rotor”, ASME. Journal of Turbomachinery, 120(1), p131-140. [https://doi.org/10.1115/1.2841374]
• Arima, T., Sonoda, T., Shirotori, M., Tamura, A., and Kikuchi, K., (1999), “A Numerical Investigation of Transonic Axial Compressor Rotor Flow Using a Low-Reynolds-Number k-Turbulence Model”, ASME Journal of Turbomachinery, 121(1), p44-58. [https://doi.org/10.1115/1.2841233]
• Madsen, J. I., Shyy, W., and Haftka, R. T., (2000), “Response Surface Techniques for Diffuser Shape Optimization”, AIAA Journal, 38(9), p1512-1518. [https://doi.org/10.2514/2.1160]
• Sevant, N. E., Bloor, M. I. G., and Wilson, M. J., (2000), “Areodynamic Design of a Flying Wing Using Response Surface Methodology”, Journal of Aircraft, 37(4), p562-569. [https://doi.org/10.2514/2.2665]
• Marz, J., Hah, C., and Neise, W., (2002), “An Experimental and Numerical Investigation into the mechanisms of rotating Instability”, Journal of Turbomachinery, 124(3), p367-374. [https://doi.org/10.1115/1.1460915]
• Chunill, Hah, (2009), “Large Eddy Simulation of Transonic Flow Field in NASA Rotor 37”, NASA/TM-2009-215627.
• Ahn, C. S., and Kim, K. W., (2003), “Design Optimization of An Axial-Flow Compressor Rotor Using Response Surface Method”, Proceedings of the Institution of Mechanical Engineerings. Part A-J. Power and Energy, 217(2), p179-184.
• Moon, Y. L., Cho, T. M., and Kim, D. K., (2000), “Nonparametric Regression Estimation for Hydrologic Application”, Proceeding of KSCE, 3, p111-114.
• Kang, H. S., Lee, J. M., and Kim, Y. J., (2015), “Shape Optimization of High Power Centrifugal Compressor Using Multi-Objectives Optimal Method”, Transaction of the KSME B, 39(5), p435-441. [https://doi.org/10.3795/ksme-b.2015.39.5.435]