질량유량 증폭기 형상변화에 따른 유동 특성 연구
Abstract
Mass flow amplifier, which is an aerodynamic device, makes air flow increased by ejecting small amount of compressed air with Coandă effect. In this study, the flow characteristics of a mass flow amplifier were studied with various flow conditions and geometrical configurations. In order to improve the performance of mass flow amplifier, various values of clearance, diffuser angle and the aspect ratio of induced flow inlet to outlet were considered as design parameter. Furthermore, four different pressure conditions of compressed air were also considered. Numerical study was performed using the commercial CFD code, ANSYS CFX 14.5 with shear stress transport(SST) turbulent model. The results of pressure and velocity distributions were graphically depicted with different geometrical configurations and operating conditions.
Keywords:
Mass Flow Amplifier, Coandă Effect, Venturi Effect, Clearance, Diffuser Angle, Aspect Ratio, CFD키워드:
질량유량 증폭기, 코안다 효과, 벤츄리 효과, 틈새, 확산각, 직경비, 전산유체역학1. 서 론
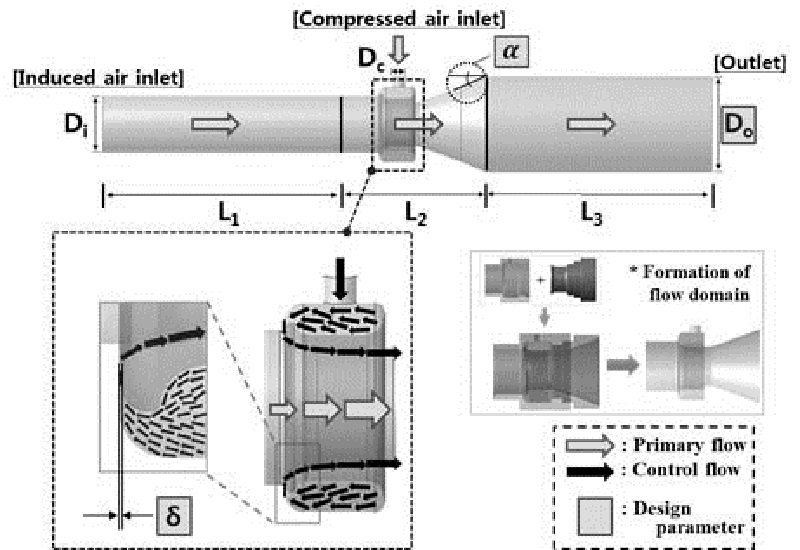
반도체 공정의 주요 이슈 중 하나는 공정 전후의 청정상태를 유지하는 것이다. 공정과정에서 증류 및 승화, 그리고 화학반응 등에 의해 고체 입자로 구성된 에어로졸 형태의 가스가 형성되는데, 이를 퓸(fume)이라 한다. 모든 산업 공정에서 발생되는 퓸은 생산 수율 및 공정 효율에 영향을 준다. 기존 공정 내에서, 퓸을 배기시키기 위해 홴(fan)과 이젝터(ejector)가 사용된다. 질량유량 증폭기(mass flow amplifier)는 다양한 공기역학 장치 중 하나로, 소량의 압축공기를 이용하여 공기흐름을 증가시킨다. Fig. 1은 다양한 산업공정에 사용되는 질량유량 증폭기를 나타낸다. 두 개의 구성품을 통합시킴으로써, 고리형태의 고압실과 환형 틈새가 생성된다. 질량유량 증폭기는 홴과 비교하여 크기가 작고 가볍기 때문에 휴대성이 좋고 반도체 공정에 용이하게 사용되고 있다. 또한 이젝터와 비교시 소량의 압축공기를 이용하여 많은 공기흐름을 유도하는 특성을 갖는다.
질량유량 증폭기는 다른 장비들보다 더욱 균일한 공기 이송을 이끌어내기 때문에, 제품 냉각, 부품의 청소 및 세척, 용접 작업, 밀폐공간 환기 등 다양한 분야에 적용되고 있다.
일반적인 질량유량 증폭기는 코안다 효과(Coandă effect)를 이용하여 작동된다. 코안다 효과란 움직이는 기체의 유동이 인접한 벽면에 밀착하여 흐르는 현상을 말한다(1). 다수의 연구자들에 의해 코안다 효과가 적용된 많은 장치들의 성능 향상 및 내부 유동을 위한 연구가 수행되었다. Ha 등(2)은 코안다 노즐의 중심 축소관 유무에 따라 화력발전의 MILD (Moderate and Intense Low Oxygen Dilution)연소에서 고온의 배기가스를 연소로 내에 재순환하기 위한 연구를 수행하였다. Manou와 Khalid(3)은 코안다 제트(Coandă jet)와 제트 플랩(jet flap) 존재 여부 및 유입 각도에 따른 풍력 터빈의 에어포일이 갖는 공기역학적 성능을 연구하였다. 그 외 많은 연구자들에 의해 코안다 효과에 의한 유동 특성이 연구된 바 있다(4-6).
질량유량 증폭기에는 또한 벤츄리 효과(Venturi effect)가 적용된다. 벤츄리 효과는 횡방향 단면적의 넓이 변화로 압력차이가 발생해 유속 또는 유량의 증가를 가져온다. Blocken 등(7)은 자연적인 환기성능 향상을 위하여 벤츄리 효과를 일으키는 형상을 지닌 지붕을 제작하여 건물 밀집 지역 내에서 지붕 높이에 따른 부압 및 유속을 실험적으로 고찰하였고, 수치 연구를 통하여 다양한 지붕 높이에 따른 환기 성능을 연구하였다. Gorjibandpy와 Sangsereki(8)는 이러한 유동특성을 이용하여 연료 혼합기에 적용하였다. Bashir 등(9)은 다양한 형상을 지닌 벤츄리 관의 공기역학적 성능을 수치적으로 연구하였다. 질량유량 증폭기를 적용한 수치 해석 및 실험 연구가 많이 수행되었지만, 이송 유량 증대와 같은 성능 향상 연구는 상대적으로 미미하다. 따라서 본 연구에서는 다양한 압력조건을 부여하여 질량유량 증폭기의 형상변화(틈새, 배관의 직경비, 후방 디퓨져 각도)에 따른 유동 특성을 수치적으로 고찰하였다.
2. 수치해석
2.1 해석모델
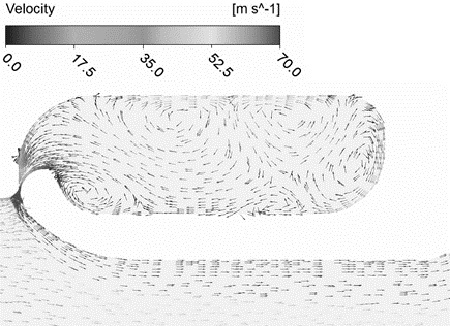
Fig. 2는 본 연구에서 사용한 질량유량 증폭기 내부의 유동영역을 나타낸다. 중앙에는 질량유량 증폭기가 배치되어있고 가로방향 양 끝으로 지름이 다른 원통이 연결되어있다. 이는 질량유량 증폭기 내부의 코안다 효과를 더욱 가시적으로 나타내기 위함으로써 기존 모델의 양끝 부분을 각각 150mm 확장시켰다. 또한 질량유량 증폭기 내 환형 고압실과 배관 사이의 좁은 틈새가 형성되는데, 이를 통해 유선방향으로 코안다 효과가 생성된다(Fig. 3 참조). 그 밖의 상세 치수는 Table 1에 기술하였다.
2.2 격자계 및 경계조건
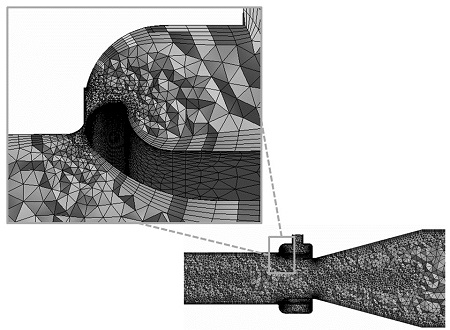
다양한 형상 변화에 따른 질량유량 증폭기의 공력성능을 파악하기 위해 연속방정식과 운동량방정식을 지배방정식으로 선택하였고 지배방정식의 해를 구하기 위하여 유한체적법을 적용하였다. 작동유체는 이상기체이고, 난류모델은 SST(Shear Stress Transport) 모델을 사용하였는데, 이는 벽면 주변에서 κ-ω 모델을, 경계층 내에서는 κ-ϵ 모델을 사용하여 유동박리 예측을 가능하게 한다. 경계조건 변화에 따른 유동 특성을 해석하기 위해 사면체로 구성된 비정렬 격자계를 구성하였으며 정확한 경계층 모사를 위해 인플레이션 격자조건을 적용하여 7겹의 격자층을 생성하였다. 격자수는 800만개로 Fig. 4에 도시하였고, 경계조건은 Table 2에 명시하였다. 수치해석은 상용코드인 ANSYS CFX ver. 16.0을 사용하였고 수렴조건으로 RMS 잔류치가 10-4 이하일 때로 설정하였다.
2.3 지배방정식
질량유량 증폭기의 유동특성을 고찰하기 위해 다음과 같은 지배방정식을 이용하였다.
- 연속방정식:
| (1) |
- 운동량방정식:
| (2) |
여기서,
| (3) |
위 식에서 ρ는 밀도, ui는 직각속도, p는 정압, τij는 인장응력, μ는 점성계수, 그리고 δij는 Kronecker delta함수를 각각 나타낸다.
3. 결과 및 고찰
3.1 틈새 변화
Fig. 5에 틈새(δ) 변화에 따른 전압력 분포를 도시하였는데, 코안다 효과에 의해 벽면을 타고 흐르는 유량이 증가함을 알 수 있다. 이는 틈새 증가에 따라 코안다 노즐 사이로 유동이 더욱 쉽게 흐르는 현상에 의한 것으로 확인된다(붉은색 원 표시). 또한 유로내부 압력구배가 크게 나타남을 확인할 수 있다.
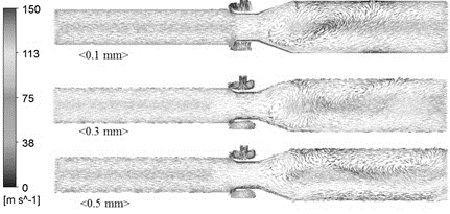
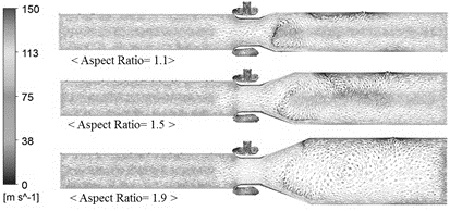
틈새 변화에 따른 내부 속도 분포를 Fig. 6에 나타내었다. 틈새가 일정 이상 증가하면 후방 유로에서 와류장 등 이차유동(secondary flow)이 발생함을 알 수 있다. 특히 틈새가 δ=0.5mm인 경우, 인가압력 반대편 벽면을 타고 흐르는 코안다 유동이 크게 발달함을 알 수 있다.
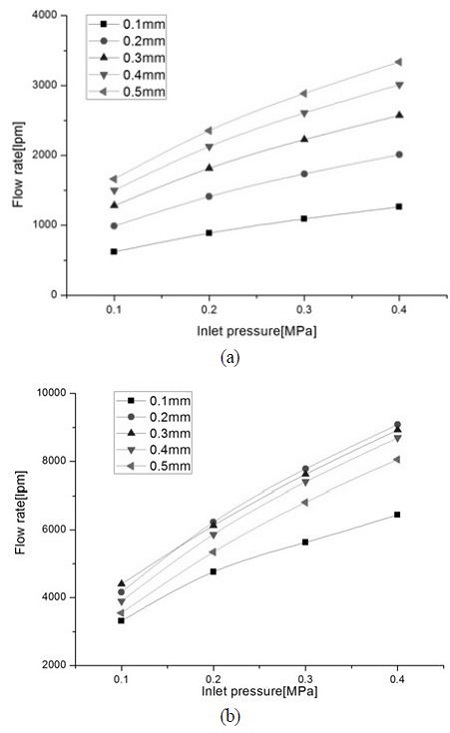
Fig. 7(a)와 (b)는 틈새 변화에 따른 압축공기 유입구로 유입되는 유량 및 유도공기 유입구로 유입되는 유량을 나타낸다. 틈새가 증가할수록 압축공기 유입구로 유입되는 작동유체의 유량이 증가함을 확인할 수 있고, 질량유량 증폭기에 의해 유도된 공기량과 틈새 사이에는 서로 비선형적인 관계를 나타낸다. 특히, 틈새가 δ=0.2mm일 때 가장 큰 값을 보이며, 이 후 틈새 증가에 따라 유도 유량이 감소하는 추세를 나타낸다. 틈새 증가에 의한 과도한 코안다 유동 증가는 유로 내부의 저압영역 생성을 억제하고 토출유로 체적을 크게 차지하는 작용을 하게 되며, 이로 인하여 유도되는 공기량 감소 현상이 발생함을 알 수 있다. 즉, 틈새가 δ=0.2mm일 경우 가장 큰 유도 공기량을 확보할 수 있다.
3.2 직경비 변화
출구 직경 변화를 고려한 다양한 직경비(Do/Di)에 따른 내부 전압력 분포를 Fig. 8에 도시하였다. 직경비 증가에 따라 유입구 인접 영역에서 전압력이 증가하는 것을 확인할 수 있었고, 전방에서는 전압력 분포가 일정한 경향을 나타내었다. 이에 반해 후방에서는 와류장 형성 등 난기류에 의한 변동이 크게 발생함을 알 수 있다. 이는 벽면을 따라 흐르는 코안다 유동 측으로 주유동이 편승되는 현상에 의한 것으로, 다음의 두 가지 현상이 함께 발생할 수 있다. 첫째, 코안다 유동 측으로 주유동이 함께 쏠리는 현상에 의하여 벽면측에는 고압영역, 유로 중심부에는 저압영역이 형성된다. 또한 코안다 유동의 벽면 부착 효과가 소진되는 시점에서부터 유동 불안정성이 증가하게 된다.
Fig. 9에 직경비 변화에 따른 내부 속도 분포를 도시하였다. 틈새로부터 분사된 유동이 코안다 효과로 인해 벽면을 따라 흐르는 현상이 발생하였다. 또한 하류 영역에서 복잡하고 변동이 심한 유속분포를 확인 할 수 있다.
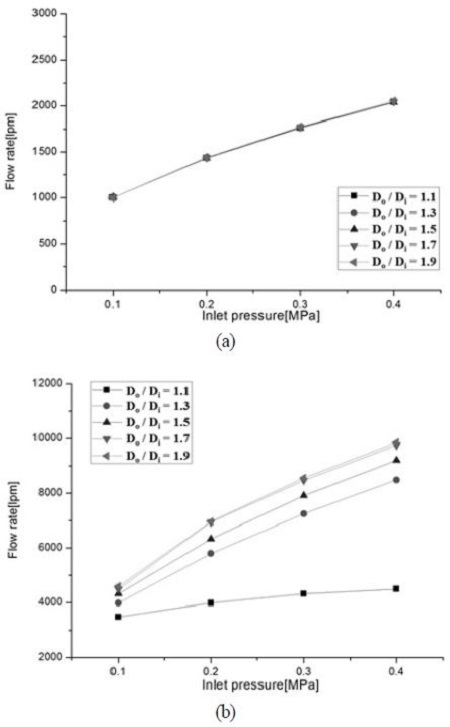
Fig. 10은 직경비 변화에 따른 압축공기 유입구와 유도 공기 유입구에서의 유량을 나타낸다. 인가 압력이 증가함에 따라 유도공기 유입구에서 유도유량이 증가함을 알 수 있으며, 이를 다시 직경비 변화에 따라 비교해보면 직경비가 증가함에 따라 유도유량도 증가함을 알 수 있다. 직경비가 Do/Di=1.1인 경우 유도유량이 현저히 감소하는 것을 알 수 있는데, 이는 저압영역이 충분하게 분포할 수 있는 공간 부재에 의한 것으로 유추할 수 있다.
3.3 확산각 영향
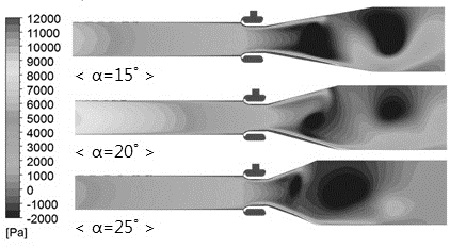
질량유량 증폭기 후방영역의 확산각(α) 변화에 따른 전압력 분포를 Fig. 11에 나타내었다. 확산각 축소에 따라 유입구 인접 영역의 전압력이 변화하는 것을 알 수 있는데, 이는 확산각 변화에 따른 유도유량의 증감에 기인하는 것이다. 본 연구에서 고찰한 세 가지 경우 중 α = 20°인 경우 유입구에서 가장 큰 전압력 분포가 나타났다. 또한 Fig. 8의 결과에서 유추할 수 있는 것처럼 벽면을 따라 흐르는 코안다 유동 측으로 주 유동이 함께 편향되는 현상에 의하여 코안다 노즐 후방에서 유동의 섭동(perturbation) 현상이 발생함을 알 수 있다. 확장각이 축소될수록 코안다 유동이 더욱 멀리 떨어져 있는 후방영역까지 도달할 수 있음을 알 수 있으며, 이러한 변화가 유도유량 변화에 영향을 미침을 확인할 수 있다.
Fig. 12은 확산각 변화에 따른 질량유량 증폭기 내부에서의 속도 분포이다. 확산각이 감소하면서 코안다 유동에 의한 고속유동이 최종적으로 도달하는 거리가 멀어지는 것을 확인할 수 있는데, 이는 확산각 감소에 따라 코안다 유동의 변화 폭이 작아지기 때문이다.
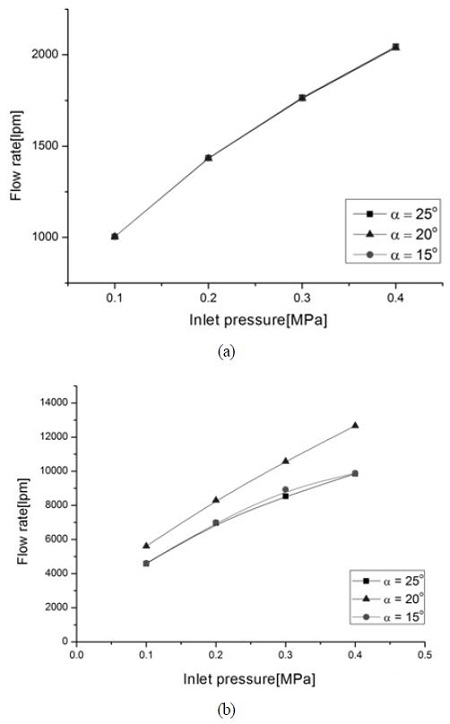
Fig. 13은 확산각 및 인가압력 변화에 따른 압축공기와 유도공기 유입구에서 각각 측정한 유량을 도시한 것이다. 인가압력 증가에 따라 유도유량이 증가함을 확인할 수 있으며, 이를 확산각에 따라 비교해보면 α = 20°인 경우 가장 큰 유도유량이 발생하였다. 따라서 α = 20∼ 25°영역에서 대유량을 확보할 수 있는 최적 확산각을 도출할 수 있는 가능성이 있으므로, 이를 위해 조금 더 세밀한 확산각 변수변화를 통한 연구가 필요함을 알 수 있다.
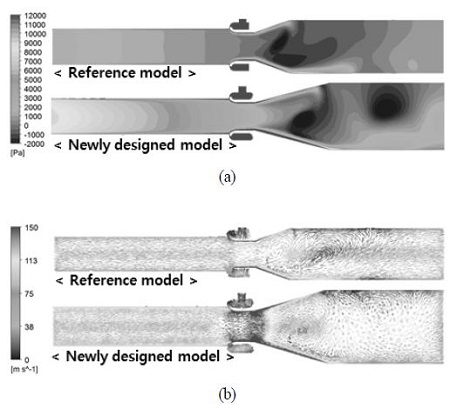
또한 최적모델과 기준모델 내부의 전압력과 속도 분포를 Fig. 14에 도시하였다. 최적화를 통한 결과로, 유도공기 유입구 지역의 전압력 증가로 인해 토출구 지역의 전압력 강하가 높아짐을 알 수 있다. 이를 통해, 유도공기 유입구에서 토출구로 향하는 유동 및 유속이 상승됨을 알 수 있다.
4. 결 론
본 연구에서는 질량유량 증폭기에 대한 세 가지 기하학적 형상변수(틈새, 직경비, 확산각) 변화를 통한 연구를 수행하였다. 틈새 변화를 통한 성능특성 고찰 결과 틈새가 δ=0.2mm일 때 가장 성능이 우수하였다. 직경비 변화에서는 토출구 직경 증가에 따른 후방유동 안정화에 의해 토출 유량이 증가하는 것을 알 수 있었으며, 압력분포를 통하여 후방영역에서 발생하는 흡입력이 직경비 Do/Di=1.9의 경우 가장 큰 값을 나타내었다.
본 연구에서 고찰한 다양한 형상 변수 중 틈새가 δ=0.2mm이고 직경비가 Do/Di=1.9일 때 확산각이 α = 20°인 경우 가장 큰 토출 유량을 나타내었다.
기 호 설 명
| Dc : | : 압축공기 유입구 지름 |
| Di : | : 유도된 공기 유입구 지름 |
| Do : | : 토출구 직경 |
| L1 : | : 전방 확장영역 길이 |
| L2 : | : 질량 유량 증폭기 길이 |
| L3 : | : 후방 확장영역 길이 |
| δ : | : 틈새 |
| α : | : 디퓨져 확산각 |
Acknowledgments
본 연구는 중소기업청 도약기술개발사업(과제번호: C0278478)의 일환으로 수행하였으며, 관계자 여러분께 감사 말씀드립니다.
References
-
Natarajan, E., and Onubogu, N. O., (2012), “Application of Coandă effect in robots – a review”, Mechanical Engineering and Technology, Advances in Intelligent and Soft Computing, 125, p411-418.
[https://doi.org/10.1007/978-3-642-27329-2_56]

-
Ha, J. S., and Shim, S. H., (2014), “Characteristic of Entrainment Flow Rate in a Coandă Nozzle with or without Coaxial contractor”, Journal of the Korean Institute of Gas, 18(2), p21-27, (in Korean).
[https://doi.org/10.7842/kigas.2014.18.2.21]

- Mamou, M., and Khalid, M., (2007), “Steady and unsteady flow simulation of a combined jet flap and Coandă jet effects on a 2D airfoil aerodynamic performance”, Revue des Energies Renouvelables CER, p55-60.
- Horn, P. E., (1996), “Air Amplifier Web Cleaning System”, United States Patent 5490300.
-
Lee, D. W., Hwang, J. G., Kwon, Y. D., Kwon, S. B., Kim, G. Y., and Lee, D. E., (2007), “A study on the air knife flow with Coandă effect”, Journal of Mechanical Science and Technology, 21(12), p2214-2220.
[https://doi.org/10.1007/BF03177482]

- Fišer, J., Jedelský, J., Vach, T., Forman, M., and Jicha, M., (2012), “Comparison of CFD simulations and measurements of flow affected by Coandă effect”, EPJ Web of Conferences, 25, Id. 01015.
-
Blocken, B., van Hooff, T., Aanen, B., and Bronsema, B., (2011), “Computational analysis of the performance of a venturi-shaped roof for natural ventilation: Venturieffect versus wind-blocking effect”, Computer & Fluids, 48(1), p202-213.
[https://doi.org/10.1016/j.compfluid.2011.04.012]

- Gorjibandpy, M., and Sangsereki, M. K., (2010), “Computational Investigation of Air-Gas Venturi Mixer for Powered Bi-Fuel Diesel Engine”, World Academy of Science, Engineering and Technology, 4, p273-277.
-
Bashir, T. A., Soni, A. G., Mahulkar, A. V., and Aniruddha, B. P., (2011), “The CFD driven optimization of a modified Venturi for cavitational activity”, The Canadian Journal of Chemical Engineering, 89(6), p1366-1375.
[https://doi.org/10.1002/cjce.20500]