A Study on the Design Method to Optimize an Impeller of Centrifugal Compressor
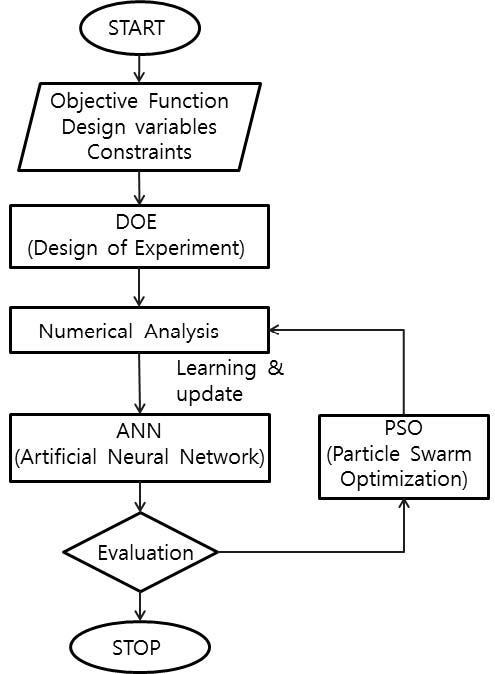
A numerical study was conducted to improve the performance of an impeller of centrifugal compressor. Nine design variables were chosen with constraints. Only meridional contours and blade profile were adjusted. ANN (Artificial Neural Net) was adopted as a main optimization algorithm with PSO (Particle Swarm Optimization) in order to reduce the optimization time. At first, ANN was learned and trained with the design variable sets which were obtained using DOE (Design of Experiment). This ANN was continuously improved its accuracy for each generation of which population was one hundred. New design variable set in each generation was selected using a non-gradient based method of PSO in order to obtain the global optimized result. After 7th generation, the prediction difference of efficiency and pressure ratio between ANN and CFD was less than 0.6%. From more than 1,200 design variable sets, a pareto of efficiency versus pressure ratio was obtained and an optimized result was selected based on the multi-objective function. On this optimized impeller, the efficiency and pressure ratio were improved by 1% and 9.3%, respectively.
Keywords:
Centrifugal Compressor, Optimization, Artificial Neural Net, Design of Experiment, Impeller Design, 원심압축기, 최적화, 인공지능, 실험계획법, 임펠러설계1. 서 론
원심압축기는 비속도가 낮은 영역에서 양호한 작동성능을 나타내므로 비교적 소형의 엔진 및 터보챠저 등에 많이 적용되고 있다. 축류형 압축기에 비하여 단당 압축비가 높고, 동일한 회전수에서 축류형에 비하여 공기유량의 변화폭이 넓은 장점이 있으며 제작이 비교적 간단한 장점이 있다. 원심압축기는 임펠러와 디퓨저로 구성되며, 임펠러의 회전운동이 흡입공기에 운동에너지를 가하고 디퓨저에서는 운동에너지를 압력으로 변환한다. 디퓨저를 나온 고압의 공기는 스크롤을 통하여 다른 장치로 고압의 공기를 전달하도록 되어 있으며, 작동조건의 변화가 많은 경우에는 디퓨저에 베인을 설치하지 않고 사용한다.
압축기의 효율과 작동안정성에 직접적인 영향을 미치는 임펠러 설계에 관한 연구는 많은 연구자에 의하여 오래전부터 수행되어 왔다. 설계 시 형상에 관한 제한사항 및 설계기법에 관하여서는 참고문헌(1-3)에 자세히 나와 있다. 하지만 사용되고 있는 임펠러의 형상이 동급에서도 서로 상이한 형상을 갖는 이유는 대부분의 설계에서 설계자의 경험과 직관에 의하여 형상설계가 이루어지기도 하지만 임펠러 설계 시에 조정 가능한 설계변수가 많은 영향도 있다.
임펠러 설계 시에 설계점에 도달하는 목표로 설계를 하지만 최종적으로는 고효율의 임펠러를 얻고자 하는 것이다. 따라서 효율을 높이기 위하여서는 임펠러에서의 손실을 줄이기 위한 유로의 형성과 블레이드를 형상화하여야 한다. 이를 위하여 형상과 관련된 변수를 선정하여 이들 변수의 변경에 따른 영향을 평가하여 형상설계를 수행하는 방식이 연구되어지고 있다. 이 과정에서 다양한 최적화기법을 활용한 연구(4-9)가 수행되고 있다. 이들 연구의 특징은 임펠러에서 형상변수의 변경에 따른 출력의 영향이 선형적으로 변하지 않으므로 전역적인 변화를 확인할 수 있는 알고리즘을 적용하고 있다.
본 연구에서는 연료전지의 시스템 효율향상을 위하여 적용되는 10kW급 원심압축기에서의 성능개선 연구가 수행되었다. 이를 위하여 임펠러 설계점에서의 압력비와 효율 향상을 위하여 압력비와 효율을 연계한 목적함수를 설정하고 유로와 블레이드를 변경하여 전역적인 향상이 되도록 하였다. 목적함수의 전역적인 탐색과 이를 위한 시간 단축을 위하여 유전자알고리즘의 일종인 PSO (Particel Swarm Optimization) 기법의 적용과 인공지능(ANN: Artificial Neural net)의 기법을 혼합한 알고리즘을 사용하였다.
2. 최적화할 압축기 임펠러
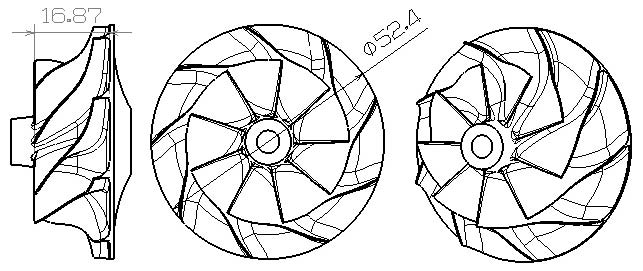
기존 설계방식으로 설계되어져 사용 중인 임펠러의 형상을 Fig. 1에서 보여주고 있으며 임펠러의 외경은 52.4mm이다. 입구에서의 쉬라우드와 허브에서의 직경은 각각 37.5mm와 11.4mm이다. 이 임펠러를 장착한 압축기에서의 설계점 사양을 Table 1에서 보여주고 있다. 하지만 압축기에서의 결과는 베어링손실 및 스크롤에서의 손실 등을 포함한다. 따라서 임펠러에서의 사양을 얻기 위하여 동일한 질량유량과 회전수에서 수치해석적으로 얻었다.
수치해석은 3차원 압축성 난류유동해석 상용프로그 램인 CFX-13(10)을 사용하였으며, 난류모델은 k - ∈모델을 적용하였다. 대류항은 second-order의 upwind 방식을 기본으로 하는 high resolution 방식을 적용하였다. 계산 영역은 3개를 만들어 입구영역, 임펠러영역, 출구영역으로 구분하였으며, 각각의 영역이 접하는 부분은 프로젠로터 조건으로 처리하였다. 계산영역은 하나의 유로에서 수행되었으며, 계산영역에서 회전방향으로의 경계조건은 주기조건을 주었다.
입구에는 전압력 조건과 출구에는 질량유량의 조건을 주었다. 격자 개수에 대한 테스트를 수행하여 39만개를 적용하였으며 Eckardt 임펠러의 실험결과와 비교하였을 때 상당히 잘 예측하는 결과(11)를 얻었다. 동일한 방식으로 본 연구의 임펠러에 대하여 Table 1과 동일한 작동조건에서 임펠러 입구와 디퓨저 출구를 기준으로 압력비와 등엔트로피효율은 2.46과 86.1%를 얻었다.
3. 임펠러 설계변수
임펠러의 성능을 향상하기 위하여서는 임펠러의 형상을 조정할 수 있는 적절한 형상변수를 선택하여야 한다. 임펠러의 형상을 표현할 수 있는 여러 가지 방법이 있으나 본 연구에서는 베지어 곡선으로 나타내는 법을 사용하였다. 이 경우에 베지어 곡선의 조정점을 설계변수로 선정할 수 장점이 있다. 압축기 자오면 기 준의 쉬라우드와 허브 형상을 표현하는데 6개 정도의조정점이면 복잡한 형상의 표현도 가능하였지만 본 연구에서는 설계변수의 개수를 가능한 적게 선택하기 위하여 각각 5개의 조정점을 사용하였다.
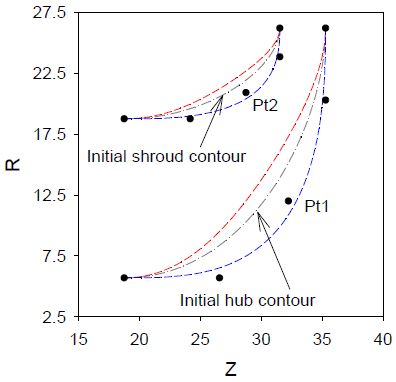
Fig. 2는 허브와 쉬라우드에서의 초기형상을 보여주고 있으며, 5개의 조정점 중에서 가운데에 있는 조정점만을 설계변수로 선정한 경우에 각각의 형상에서 변화되는 영역을 보여주고 있다. 하지만 선정된 조정점은 Z-방항(축방향)과 R-방향(반경방향)으로 이동이 가능하므로 조정점 하나 (Pt1)에서 두 개의 설계변수(φ1, φ2)를 얻게된다. 따라서 허브와 쉬라우드 형상을 조정하기 위한 설계변수는 4개가 선택되었다.
설계변수로 선정된 조정점의 이동은 제한적이어야 한다. 그렇지 않으면 케이싱에 조립되지 못하는 문제와 내부유로에서의 면적 변화가 균일하지 않는 문제를 야기하게 된다. Table 2는 허브와 쉬라우드에서의 최적화 과정에 사용된 초기모델의 조정점과 제한조건들을 보여주고 있다. Fig. 2에서 표시된 영역의 변화는 제한조건 이내에서 이동하였을 때 얻어진 결과이다.
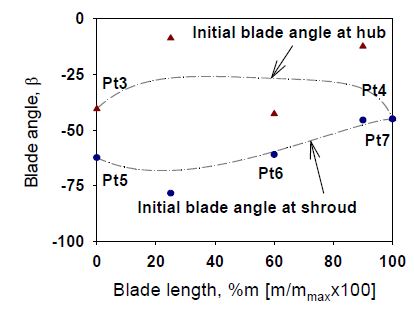
3차원 블레이드를 표현하기 위하여 블레이드 익형각(β)은 캠버선이 회전하는 각도(θ)와 자오면에서 익형의 곡선길이(m)를 이용하여 식(1)과 같이 표현된다. 따라서 허브와 쉬라우드에서 캠버선을 따라 익형각의 변화를 나타내기 위하여 베지어 곡선을 사용하였으며, 베지어 곡선의 조정점은 각각 5개를 사용하였다. 초기모델의 블레이드 익형각의 분포를 Fig. 3에서 보여주고 있다.
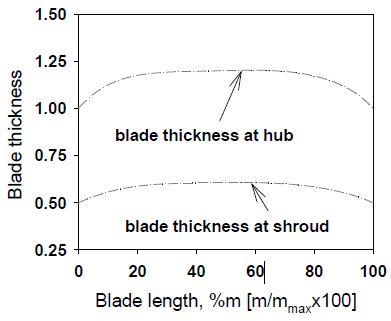
익형각의 분포에서 쉬라우드에서는 입구와 가운데 점 그리고 출구에서의 조정점을 설계점(φ7, φ8, φ9)으로 설정하여 허브보다 긴 익형길이에 대하여 익형각의 변화 폭을 넓혔으며, 허브에서는 입구와 출구의 조정점을 설계점(φ5, φ6)으로 설정하였다. 따라서 본 연구에서는 총 9개의 설계변수를 선택하였다. 아울러 익형의 형상이 공력적으로나 구조적으로 문제가 없도록 최소한의 제한조건을 정하였으며 익형각의 조정점과 제한조건을 Table 3에서 보여주고 있다. 비록 설계점의 제한범위를 설정하였다고 하여도, 임펠러에서의 익형각은 제한조건 범위내에서도 구조적으로 심각하게 뒤틀어지는 형상이 얻게 되므로 출구에서의 린(lean)각을 초기형상과 같이 얻어지도록 허브에서 설계점이 아닌 조정점들은 자동적으로 변경되도록 하였다. 아울러 익형의 두께는 초기 모델의 두께와 동일하게 분포하였으며 두께의 분포는 Fig. 4에서 보여주고 있다.
4. 최적화 기법
원심압축기의 최적화에서 통상 목적함수로 적용되는 효율이나 압력비는 설계변수의 변화에 대하여 선형적인 결과를 보여주지 않으므로 전역적인 방법을 선택하여야 한다. 하지만 전역적인 최적화방법은 많은 계산시간을 필요로 한다. 따라서 계산시간을 단축하면서 정확한 결과를 얻는 것이 중요하다. 본 연구에서는 최적화를 위한 방법으로 인공지능 방식을 기본으로 사용하였다. 인공지능은 역전파알고리즘(back propaga-tion algorithm)을 적용하였으며 은닉층과 출력층의 뉴론은 각각 10개와 2개를 사용하였다. 전달함수는 은닉층에는 hyperbolic tangent 함수를 사용하였으며, 출력층은 직선함수를 적용하였다. 인공지능망이 주어진 결과와 일치하도록 하기 위하여 가중치와 바이어스는 Levernberg-Marquardt(1213)알고리즘을 적용하여 얻었으며, 인공지능망의 형성은 MATLAB(14)의 nntool을 사용하였다.
초기의 인공지능망을 형성하기 위한 인공지능망의 입력은 9개의 설계변수로부터 실험계획법을 적용하여얻었다. 실험계획법의 적용은 설계변수의 주효과나 교호작용 등에 대한 정보를 알 수 있으며 실험의 횟수를 줄일 수 있는 효과적인 방법이기 때문이다. 본 연구에서는 부분요인배치(Fractional Factorial Design)을 시행하였으며, resolution VI 의 배치법을 적용하였다. 따라서 중심점 개수까지 포함하면 총 65개의 설계변수 세트에 대한 공간을 형성하게 된다. 따라서 65개의 설계변수 세트에 대한 수치해석결과가 필요하게 된다. 실험계획법만으로도 최적화를 수행할 수 있지만 결과가 비선형성이 강한 경우에는 실험계획법로 얻은 최종결과와 실제결과 사이에 차이가 발생할 수 있으므로 초기의 인공지능망 형성에만 적용하였다.
초기의 인공지능망이 형성되면 새로운 설계변수들의 세트에 대하여 목적함수를 찾을 수 있다. 최적의 목적함수를 찾기 위하여서는 무한한 설계변수들의 세트에서 효과적인 설계변수의 세트를 적용하여야 한다. 이를 위히여 비기울기기반의 방식인 PSO (Particle Swarm Optimization)(15)를 적용하였다. PSO의 적용에서 각 세대별 개수는 100개로 설정하였으며 다음세대를 찾기 위하여서는 초기 가중치 변수는 1.4로 하였으며, 신뢰 변수 C1과 C2는 1,5와 2,5로 설정하였다.
PSO에서 얻어진 설계변수 세트를 인공지능망에 적용하여 목적함수를 찾은 후에 우성의 결과에 대하여 서는 수치해석을 통하여 다시 결과를 획득한다. 이러한 결과들의 세트는 인공지능망의 입력으로 추가되어 인공지능망의 정확도를 향상한다. Fig. 5의 진행과정에서 보여주는 것처럼 동일한 방법으로 다음세대에 대한 설계변수의 세트를 찾고 앞서 향상된 인공지능망을 사용한다. 최종적으로 인공지능망의 정확도가 충분히 향상될 때까지 반복수행하면서 최적값을 찾게 된다.
5. 목적함수
압축기 최적화의 목적함수는 사용자에 따라서 달라질 수 있다. 즉, 고효율만을 목적으로 하거나 높은 압축비만을 목적으로 할 수 있다. 본 연구에서는 식(2)와 같이 효율(Pη)과 압축비(PII)를 동시에 고려한 목적함수(Obj)를 설정하였다.
식(2)에서 ω는 가중치(weighting function) 이다. Pη은 계산에서 얻어지는 전효율(ηt-t)과 이상적인 최대효율(100%)과의 차이를 식(3)와 같이 효율에 대한 목적함수로 설정하였다. 따라서 효율의 증대를 얻기 위하여서는 Pη은 최소화되어야 한다.
압축기의 성능을 나타내는데 있어서 효율과 마찬가지로 압축비도 중요한 인자이다. 압축비는 사용목적에 맞도록 초기에 설정되는데 사용목적에 따라 요구되는압축비보다 낮으면 문제가 된다. 또한 요구하는 압축비보다 너무 높아도 동력 손실이 증가하게 된다. 따라 서 압축비는 요구하는 압축비(IIrq)의 보다는 증가하도록 하면서 중요도는 효율에 비하여 제한을 가하였다. 식(4)와 같이 압축비의 목적함수를 설정하고 가중치는 0.3을 적용하였으며, 효율의 가중치는 1.0으로 설정하였다. 따라서 목적함수를 최소화하는 것은 압축비와 효율을 최대화하게 된다.
임펠러 익형의 익형각이 최적화과정에서 설계변수의 변화에 따라서 변경되므로 임펠러 익형에서 발생되는 기계적인 응력도 변경된다. 익형이 심하게 휘어져 응력이 허용응력을 초과하게 된다. 이러한 경우는 제한조건으로 임펠러에 가해지는 응력이 허용응력을 초과되지 않도록 하는 제한조건을 식(5)와 같이 설정하였다.
6. 최적화 과정 및 결과
인공지능에서 설계변수 세트의 입력에 대하여 출력을 효율과 압력비로 두 개를 설정하여 얻었다. 얻어진 효율과 압력비로부터 식(2)와 같은 목적함수를 얻어서 PSO에 의한 다음세대의 설계변수의 세트를 얻었다. 얻어진 설계변수의 세트를 인공지능망에 적용하여 일정이상으로 향상된 목적함수에 대하여서는 수치해석으로 재계산을 수행하였다. 각 세대별 재계산된 개수를 Table 4에서 보여주고 있다.
Table 4에서 인공지능망에서 얻어진 압력비와 효율이 재계산되어 얻어진 결과와의 정확도를 나타내고 있는데 식(6)은 참고로 효율 예측의 정확도를 계산하는 방식을 나타내고 있다. 7세대에서 압력비와 효율 예측의 정확도가 0.6% 이하로 되었음을 알 수 있다. 목적함수는 6% 정도의 정확도를 나타내는데 이는 실제 압력비와 효율의 스케일이 다르게 적용하였기 때문이다 하지만 얻고자하는 압력비와 효율의 정확도가 세대별로 향상되었으므로 인공지능망을 사용하여 최적화를 하는 것은 적절한 것으로 판단된다.
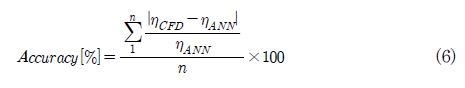
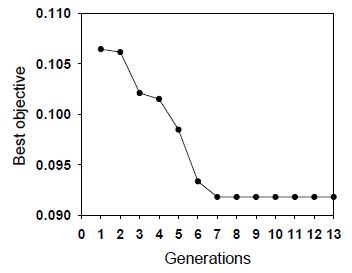
1,200번 이상의 설계변수 세트에 대하여 Fig. 6은 각 세대별에서 최소의 목적함수값을 보여주고 있다. 7세대 이후부터 목적함수가 개선되지 못하고 있음을 알 수 있으며 최소의 목적함수가 얻어진 설계변수의 세트는 Table 5와 같다. 이렇게 설계된 임펠러에서의 압력비와 효율은 각각 2.69와 87.1%가 얻어졌다. Fig. 7은 최적화된 압축기의 형상을 보여주고 있으며, 초기 임펠러에 비하여 임펠러의 입구와 출구반경 및 출구폭은 변경되지 않으면서 향상된 결과를 얻었다.
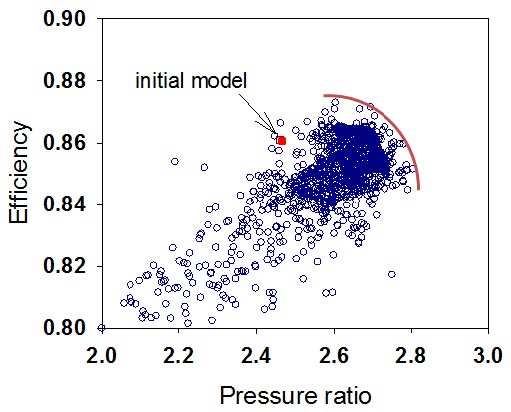
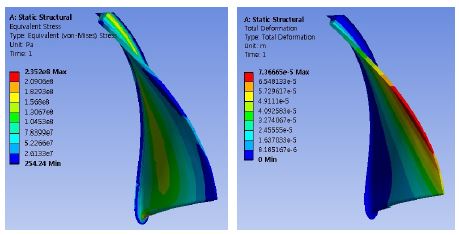
Fig. 8은 전체 설계변수 세트에 대하여 효율과 압력비의 관계를 보여주고 있다. 효율과 압력비는 상반관계를 나타내며 팔레토의 프론트 라인에 있는 설계변수는 사용자에 따라서 선택되어 사용되어질 수 있다. 최적화된 임펠러에서의 응력과 변위에 대한 결과를 Fig. 9에서 보여주고 있는데 최대변위는 팁간극의 30% 정도 수준을 보여주고 있으며, 최대응력에 대하여서는 안전율 2.1의 결과를 나타내었다.
7. 결 론
본 연구에서는 압축기의 임펠러에 대하여 여타부품의 변경이 없이 임펠러와 케이싱의 쉬라우드 형상만 변경하여 효율이나 압력비를 향상하는 연구를 수행하였다. 전역적인 최적화의 적용과 빠르게 목적함수에 접근하기 위하여 인공지능의 알고리즘을 적용하고 추가적으로 실험계획법과 PSO법을 혼합한 알고리즘을 사용하였다. 이 같은 방식으로 실제수치해석은 150여회 수행하고 총 1,200 여개의 설계변수세트에 대하여 계산을 수행하여 초기 모델에 비하여 효율은 1% 향상하고 압력비는 9.3% 향상하는 결과를 얻었다.
Acknowledgments
본 연구는 한국기계연구원에서 시행하는 일반사업의 및 기초기술연구회가 지원하고 한국항공우주연구원이 주관하는 DRC사업의 일부로 수행되었습니다.
References
- Cumpsty, N. A., “Compressor Aero-dynamics”, Longman Group UK, (1989.).
- Whitfield, A., Baines, N. C., “Design of Radial Turbomachines”, Longman Group UK, (1990.).
- Aungier, R. H., “Centrifugal Compressor”, ASME Press, (2000.).
- Bonaiuti, D., Pediroda, V., “Aero-dynamic Optimization of an Industrial Centrifugal Compressor Impeller Using Genetic Algorithms”, Proceedings of Eurogen 2001, (2001.).
- Bonaiuti, D., Arnone, A., Ermini, M., Baldassarre, L., “Analysis and Optimization of Transonic Centrifugal Compressor Impellers Using the Design of Experimental Technique”, GT-2002-30619, (2002.).
- 김세미, 박준영, 안국영, 백제현, “반응면기법을 이 용한 원심압축기 최적설계”, 한국전산유체공학 추계학술대회, (2007), p92-199.
-
Bonaiuti, D., Zangeneh, M., “On the Coupling of Inverse Design and Optimization Techniques for the Multi-objective, Multipoint Design of Turbo-machinery Blades”, J. of Turbomachinery, (2009), 131, 021014-1.
[https://doi.org/10.1115/1.2950065]

-
Verstraete, T., Alsalihi, Z., Braembussche, R.A.V., “Multidisciplinary Optimization of a Radial Compressor for Microgas Turbine Applications”, J. of Turbomachinery, (2010), 132, 031004-1.
[https://doi.org/10.1115/1.3144162]

- Kim, J. H., Choi, J. H., Husain, A., Kim, K. Y., “Multi-Objective Optimization of a Centrifugal Compressor Impeller Through Evolutionary Algorithms”, Proc. IMechE Vol. 224, Paer A:J. Power and Energy, (2010), p711-721.
- CFX-13, version 13, Ansys Inc, (2011.).
- 최형준, 박영하, 안국영, 조수용, “원심압축기 최적화를 위한 연구 I-형상변수 및 설계변수에 관한연구”, 항공우주학회지, (2011), 39(5), p424-432.
- Hagan, M. T., Menhaj., M., “Training Feed-Forward Networks with the Marquardt Algorithm”, IEEE Transactions on Neural Networks, (1999), 5(6), p989-993.
- Hagan, M. T., Demuth, H. B., Beale, M. H., “Neural Network Design”, Boston, MA: PWS Publishing, (1996.).
- Beale, M. H., Haga, M. T., Demuth, H. B., “Neural Network Toolbox, User’s Guide”, Matlab R2012a, (2012.).
- Venter, G., Sobieski, J., “Particle Swarm Optimization”, AIAA 2002-1235 , (2002.).