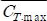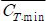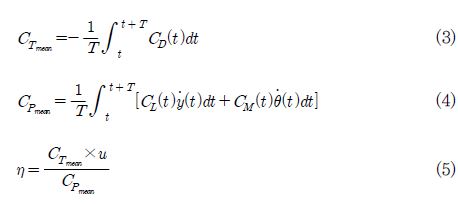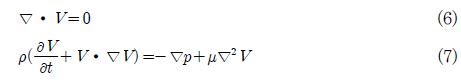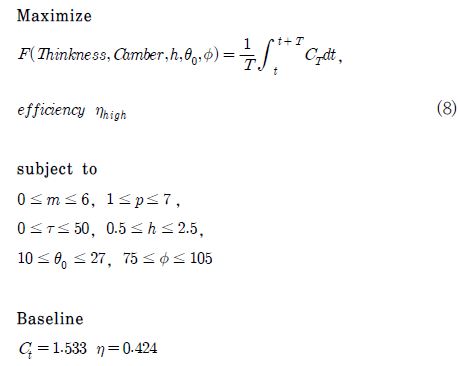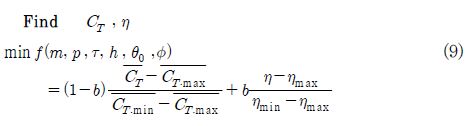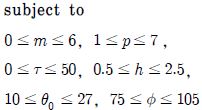Optimization Design of Hydrofoil Shape and Flapping Motion in AUV(Autonomous Underwater Vehicle)
The motion of living organisms such as birds, fishes, and insects, has been analyzed for the purpose of the design of MAV(Micro Air Vehicle) and NAV(Nano Air Vehicle). In this research, natural motion was considered to be applied to the determination of the geometry and motion of AUV(Autonomous Underwater Vehicle). The flapping motion of a number of hydrofoil shapes in AUV was studied, and at the same time, the optimization of the hydrofoil shape and flapping motion was executed that allow the highest thrust and efficiency. The harmonic motion of plunging and pitching of NACA 4 digit series models, was used for the numerical analysis. The meta model was made by using the kriging method in Optimization method and the experimental points of 49 were extracted for the OA(Orthogonal array) in DOE(Design of experiments). Parametric study using this experimental points was conducted and the results were applied to MGA(Micro Genetic Algorithm). The flow simulation model was validated to be an appropriate tool by comparing with experimental data and the optimized shape and motion of AUV was turned out to produce highest thrust and efficiency.
Keywords:
AUV, Thrust, Approximate model, Kriging method, Flapping foil, MGA, 자율무인 잠수정, 추력, 근사 모델, 크리깅 기법, 플래핑 포일, 마이크로 유전 알고리즘기호설명
m -최대 캠버(Maximum Camber)
p -최대 캠버의 위치(Location of Maximum Camber)
τ -에어포일의 두께(Thickness)
h -플런징 높이(Plunging Amplitude)
θ0 -피칭 각도(Pitching Amplitude)
ø -위상각(Phase Angle)
µ -점성계수(Viscous Coefficient)
ν -동점성계수(Kinemetic Viscosity)
η -추진효율(Propulsion Efficiency)
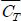 -평균 추력계수(Averaged Thrust Coefficiency)
-평균 추력계수(Averaged Thrust Coefficiency)
C -코드의 길이(Length of Chord)
1. 서 론
Autonomous underwater vehicle (AUV, 이하 자율 무인 잠수정)의 시초는 1775년 미국에서 David Bushnell와 그의 형제들에 의해 만들어졌으며 “Turtle”이라는 이름의 첫 잠수정으로 시작되었다. 그 후 19세기 말에 이르러 동력으로 움직이는 실용적인 잠수정이 만들어졌다. 이 후 계속적인 잠수정에 대한 발전이 이뤄져 현재의 어뢰를 개발하게 되었는데 이것이 자율 무인 잠수정의 시초라고 할 수 있다.
최근에는 Micro Air Vehicle(MAV, 이하 초소형 비행체), Nano Air Vehicle(NAV, 이하 나노 초소형 비행체)이 군사적 목적으로 인명피해를 줄이기 위한 탐색용과 해저지형을 탐색하는 용도로 개발되고 있다.(1) 또한 새나 곤충의 날개짓을 모방하여 MAV를 개발하는 것과 마찬가지로 자율 무인 잠수정분야에서도 물고기나 거북이등 지느러미를 가진 동물들이 물 속에서 헤엄치는 움직임들을 모사하는 연구가 진행되고 있다.
Jeffrey A. Walker는 수중 생물의 가슴 지느러미의 형상과 Rowing 운동의 특징을 도입하여 Rowing 운동과 플래핑 운동을 비교하여 수중 생물의 지느러미 움직임과 플래핑 운동에서의 운동학적, 에너지적인 부분이 유사하다고 제시하였다.(2) M.A.Ashraf는 Plunging(플런징)과 Combined motion (플런징과 피칭 운동의 조합)에서 에어포일의 두께와 캠버의 변화에 대한 효과가 추력과 효율에 영향을 미치는 것을 확인하였고, 이를 통해 Symmetric과 캠버가 결합된 에어포일에서의 최대 추력을 발생하는 형상과 효율에 대한 파라미터들을 제시했다.(3)
I. H. Tuncer는 플런징과 피칭 운동에 대해 최대 추력과 효율을 발생 시키는 형상을 확인하기 위한 최적화 방법을 수행하였다. 특히 이 연구에서 Plunge amplitude(h, 이하 플런징 높이)와 Pitch amplitude(θ0, 이하 피칭 각도)과 Phase angle(ø, 이하 위상각)에 대해 최대 추력과 효율이 발생하는 움직임에 대해 제시하였다.(4)
Stephen Licht 등이 Flapping foil(플래핑 날개)를 적용한 자율 무인 잠수정의 설계에 대해 제시하였고 이에 대해 Combined motion을 사용하여 Thrust(이하 추력)와 스트라울 수와의 관계 및 Roll amplitude(롤의 높이, pitch amplitude와 동일)에 대한 실험을 수행하였다.(5) Alexandra H.Techet이 Stephen Licht등이 제안한 모델을 가지고 움직임에 대한 추력과 스트라울 수와 플런징 높이에 대해 실험을 하였다.(6)
그러나 앞선 연구들에서는 거의 대부분 형상과 운동의 각각에 대해 개별적으로 추력과 효율만 고려하였다. 형상에서는 캠버는 양력, 두께는 추력에 지배적인 영향을 미치고, 운동에서는 플런징 높이는 추력, 피칭 높이와 위상각의 경우 값의 증감에 따라 추력과 효율이 영향을 받는 앞선 실험 및 연구의 결과가 있다. 하지만 형상과 운동의 연관성 및 종합적인 관계를 고려한 최적설계에 대한 연구가 진행되지 않았다. 따라서 본 연구에서는 플래핑 운동이 적용된 자율 무인 잠수정의 날개형상 및 운동의 연관성을 통한 최대 추력과 효율을 알아보고 이를 위해 최적화를 수행하였다.
날개형상으로는 NACA 4자리 계열의 에어포일을 사용하였고, 피칭과 플런징에 대한 혼합운동을 적용하였다. 또한 직교배열표를 이용해 각각의 실험점을 정하고 각각에 대해서 상용코드인 FLUENT를 이용하여 유동해석을 수행하였다.
이들 해석결과들을 바탕으로 Kriging method(이하 크리깅 기법)을 이용하여 근사모델을 생성하고 최적화를 수행하였다. 그 결과 최대 추력 및 효율을 얻을 수 있었고, 에어포일의 두께 및 캠버, 그리고 플래핑 운동에서의 플런징 높이 및 피칭 각도 등을 찾을 수 있었다.
2. 수학적 모델
2.1 플래핑 운동의 모델
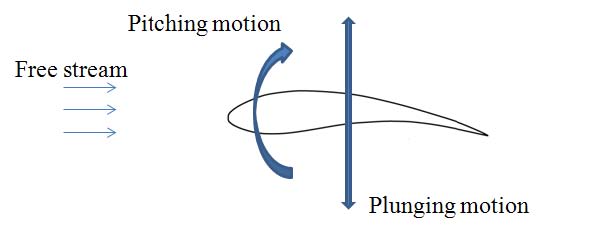
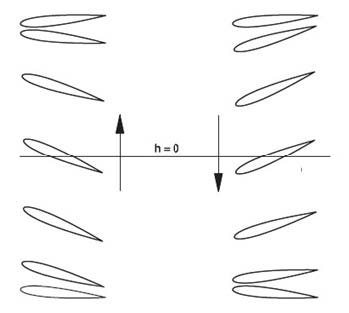
플래핑 운동은 흔히 식 (1), (2)의 플런징과 피칭 운동으로 구분된다. C는 코드의 길이, h는 플런징 높이, θ0는 피칭 각도, ø는 플런징과 피칭의 위상각을 나타내며, 본 연구에서는 Fig. 1 과 같이 두 운동이 결합된 운동을 적용한다.
자율 무인 잠수정에 적용할 때 제안한 플런징과 피칭운동을 Fig 2 에 나타내었다. 그림에서 볼 수 있듯이 피칭 운동과 플런징 운동이 적용되므로 Upstroke(이하 업 스트로크)와 Downstroke(이하 다운 스트로크)가 일어나는 동안 좌우회전이 발생되는 피칭 운동이 일어난다.
한 주기당 추력을 평균으로 표현한 식 (3)이 평균 추력계수 CTmean이고 u는 Free Stream velocity(이하, 자유 유동 속도)를 나타낸 것이다. (4)는 평균 파워계수 CPmean이며, 여기서 주기 T는 플래핑 운동의 한 주기를 나타내며, 식 (5)는 추진효율을 나타내며 평균 추력계수와 평균 파워계수를 통해 구할 수 있다.
2.2 수치해석 방법
본 연구에서는 실제 자율 무인 잠수정의 실험값과 비교하기 위해 실험에 적용된 값을 사용하며, 실험값과 비교하기 위해 사용하는 스트라울 수 0.5로 하였다. 적용되는 유체가 물이므로 이에 따른 물성치는 Table 1과 같이 정의하였다.
J. Young 등과(7) P.C Wilkins 등이(8) 플래핑 운동에 대해 NACA Airfoil(이하 에어포일) 모델에 대해2차원 Navier- Stokes 유동해석을 수행하였고 여러 레이놀즈 수에서 2차원과 3차원의 수치적 해석의 타당성을 검증하였다.
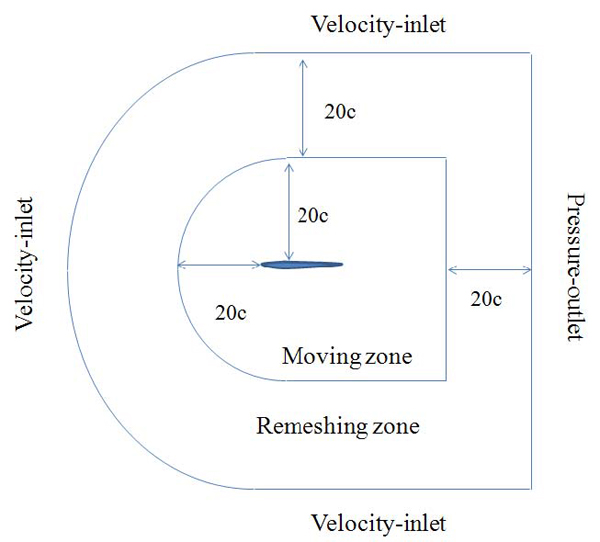
본 연구에서는 Fluent를 사용하여 2차원 비정상 유 동 해석을 수행하였다. 유동장 해석을 하기 위해 적용한 격자와 경계조건은 Fig 3과 같다. 격자는 C-Type 으로서 운동이 발생하는 Moving zone과 Remeshing zone으로 구성되어 있다. Fig 4와 5는 시간에 따른 Mesh의 변화를 나타내는 그림으로 T=0.25와 0.75일 때의 Mesh 변화 형태를 나타내고 있다. 또한 계산을 수행 시 Moving zone에 대 해 User Define Function 기능을 이용하여 앞서 언급한 식 (1), 식 (2)의 함수를 적용하였다. ∆t에 따라 시간에 따른 Remeshing의 안정성이 달라질 수 있으므로 이를 고려하여 ∆t를 선정하여야 하며, 본 연구에서 사용된 ∆t는 0.00048∼0.0009로 CFL nubmer의 조건인 식(6)을 만족하는 값임을 확인하였다.
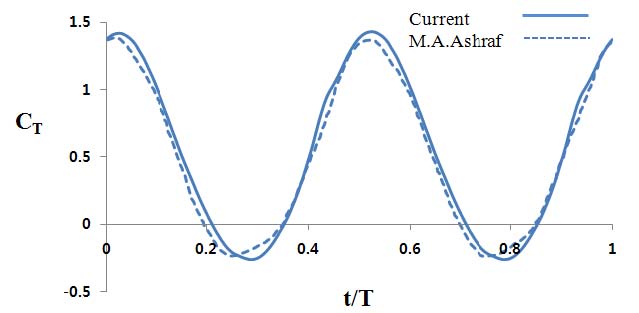
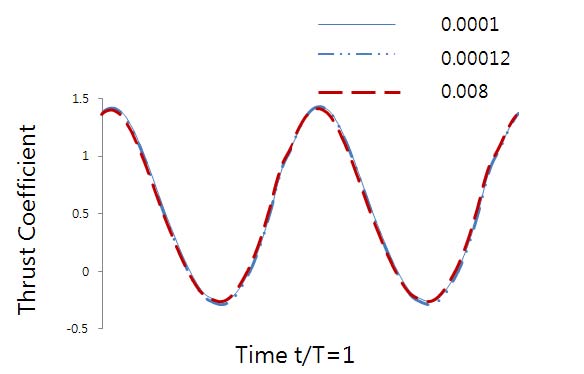
본 유동장 계산은 전 유동장이 층류영역이지만 난류 계산 수준의 공간 정확도 확보 및 작은 Vortex의 생성 및 전파를 파악하기 위해서 y+ = 1의 수준의 격자 간격을 설정하였다. 이에 따라 계산된 값이 Airfoil의 수직인 방향으로 에어포일의 0.0001배 격자 간격을 부여하였다. 추가적으로 Fig 7에서 볼 수 있듯이 Grid independent test를 통해 0.0001배 이상인 경우에 값이 안정적으로 도출되어 0.0001배로 설정하였다. Fig 6는 NACA 0030의 모델로 C-topology Grid를 적용하였으며, 유동장 조건은 K=2, h=0.5, 그리고 Reynolds number는 20000으로 설정하여 본 연구에서 적용한 Grid 형태와 Motion에 대한 Validation을 수행하였다. Fig 8은 본 연구에서 적용한 수치해석 방법과 실험 해석 결과와의 비교 검증을 하기 위해 실험 해석에 적용한 유동장 조건을 동일하게 적용하여 주기성의 유사함을 확인하였다.
3. 최적화
3.1 설계 문제의 정식화
앞서 제안한 플런징과 피칭을 조합한 운동에서 높은 추력과 효율을 얻기 위해 다음과 같이 설계 문제를 정식화하였다.
여기서 최대 캠버, 최대 캠버의 위치, 두께, 플런징 높이, 피칭 각도, 위상차를 선정하였다. 목적함수는 다목적함수로 6가지의 설계변수로부터 추력과 효율을 최대화하는 함수이다. 제한 조건으로는 Joel E. Guerrero(10) 와 M. A. Ashraf(3) 가 제시한 두께와 캠버의 크기에 따른 추력 및 효율 변화의 내용을 참고하여 에어포일에 관한 제한 조건은 에어포일에 대한 Non-symmetric 형태를 고려하여 최대 캠버, 최대 캠버의 위치를 설정하였다. h, ø, θ0의 설계 변수는 I.
Tuncer(4)가 초소형 비행체의 추력과 효율에 관한 최적화를 다룬 내용을 참조하여 설정하였다.
최적화 값의 기준이 되는 값은 스트라울 수 0.5에서 가장 높은 추력을 나타낸 값과 효율을 기준으로 하여 최적화를 수행하였다.
3.2 실험계획법(DOE)과 근사 모델
플래핑 운동을 통해 추력과 효율을 최대화하기 위해 형상과 운동을 결정하는 변수를 설계변수로 하여 근사모델을 사용하였다. DOE: Design of experiments(이하 실험계획법)방법 중에 Orthogonal array(이하 직교 배열표)를 사용하였고 근사모델을 만들기 위해 크리깅 기법을 적용하였다.
직교배열표는 실험을 위한 표본점을 생성하는데 사용되며, 유동 해석을 위해 Table 2와 같이 각 설계변수를 7개의 수준으로 나누고 L49직교 배열표를 이용하여 표본점 49개를 생성하였다. 각 Type에 대한 설명은 기호설명을 참조하기 바란다.
본 연구에서는 근사모델로서 크리깅 모델을 적용하였다. 크리깅 모델은 구하고자 하는 미지 값을 알고 있는 주위 값들의 가중선형조합으로 예측하는 방법으로 비선형성이 큰 경우에 대해 매우 효과적으로 표현이 가능하다.(11)
따라서 높은 추력과 효율을 얻기 위한 형상과 움직임에 대한 최적화를 위해 평균 추력, 양력 그리고 모멘트 계수 등의 결과를 각각 크리깅 기법을 이용하여 근사모델을 생성하였다.
또한 앞서 정의한 설계 문제에 따라 최적화를 수행하였으며 최적화는 수행시 PIAnO의 MGA(Micro Genetic Algorithm, 이하 마이크로 유전 알고리즘)을 사용하였다.
4. 결과
4.1 실험계획법에 의한 영향도 및 수치해석 분석
먼저 직교 배열표를 이용하여 49개의 표본점을 생성한 내용을 토대로 Parametric study(이하 파라메트릭 스터디)를 한 결과 중 추력 및 효율의 상위 값을 나타내는 6개의 형상을 위주로 Table 3에 나타내었다.
Table 3에서 알 수 있듯이 최대 추력을 나타내는 형상은 NACA 6235이고 플런징 높이 0.5, 피칭 높이 24 위상차는 90인 플래핑 운동에서 발생하였다. 반면에 효율은 NACA 4330에서 가장 높은 값이 발생하였고 플런징 높이 2.5, 피칭 높이 12, 위상차는 85인 플래핑 운동에서 발생하였다. NACA 4330에 대한 추력 값과 효율이 고르게 좋은 값을 보인 것이 큰 특징임을 알 수 있었다. 그리고 플런징 높이나 위상각 에어포일 형상 등이 일정하게 나타나는 특징도 볼 수 있었다.
추력과 효율이 높은 두 형상의 특징을 살펴보면 NACA 6320의 경우 플런징 높이, 위상각의 영향으로 높은 추력이 나왔지만 캠버의 영향으로 양력이 높아져 효율이 낮게 나온 원인이 되었다. NACA 4330은 두께와 위상각 및 적절한 캠버 두께와 위치의 영향으로 높은 효율과 추력이 발생하였다.
또한 추력을 발생시키는 파라미터는 무 차원 진동수와 스트라울 수, 피치 각도, 위상각 등에 관련이 있고 양력에 관한 것은 형상과 관련이 있다는 것을 확인할 수 있었다.(10)
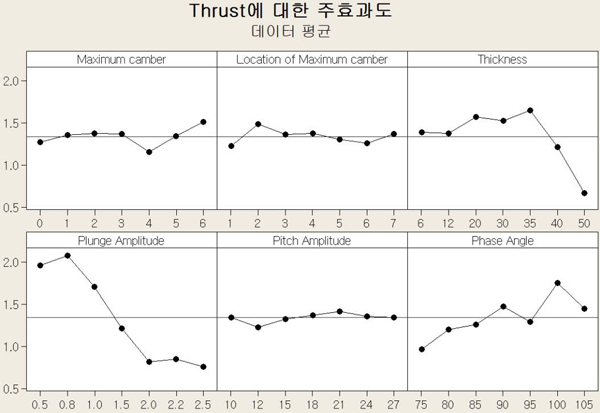
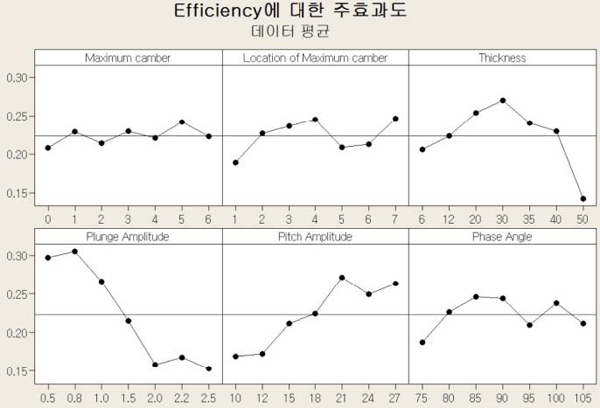
Fig 9 과 10은 추력과 효율에 대한 설계 변수의 반응도를 살펴보기 위해 Minitab 16의 ANOVA 주효과도를 수행하여 앞서 최적화를 수행하기 위해 파라메트릭 스터디에 적용했던 변수들의 범위 중에 가장 영향도가 높은 값을 확인하였다.
Fig 9는 추력만 고려하였을 때 최대 추력 값을 발생 시키는 각각 변수마다의 값들을 알아본 것이다. 먼저, 캠버의 최대 두께의 관한 경우 6, 최대 두께의 캠버 위치는 2, 두께는 35, 플런징 높이는 0.8, 피칭 각도는 21, 위상각은 100의 값들이 가장 좋은 추력을 나타내었다.
더하여 Fig 10에서 볼 수 있듯이 효율에 관한 경우에는 캠버의 최대 두께 5, 최대 두께의 캠버 위치는 7, 두께는 30, 플런징 높이 0.8, 피칭 각도 21, 위상각은 85의 값들이 최대 효율을 가짐을 알 수 있었고, 최적의 효율을 가지는 형상과 운동은 최적의 추력을 가지는 형상과 운동과는 다르다는 것을 확인하였다. 높은 추력과 효율을 동시에 만족 시키는 형상과 운동을 찾기 위해 근사 모델을 바탕으로 마이크로 유전 알고리즘을 이용하였다.
4.2 근사 모델을 이용한 최적화
직교배열표을 통한 파라메트릭 스터디 결과 값을 검증하기 위해 PIAnO 프로그램에서 DO(Design optimization)을 수행하였다. 크리깅 기법에 의한 근사 모델을 기반으로 하였으며 Methodology는 Direct search를 Method는 최적화 설계 시에 여러 조건을 만족하는 최적의 값들을 찾는 것이 매우 어렵기 때문에 자연 진화의 알고리즘을 이용한 우월한 유전자 즉, 최적의 값을 찾는 기법인 마이크로 유전 알고리즘을 적용하였다.(12) 마이크로 유전 알고리즘을 통한 결과를 Table 4로 나타내었다.
시뮬레이션 값이 비선형적이고 값의 차이가 크기 때문에 마이크로 유전 알고리즘을 적용하기 어려움이 있다.
따라서 크리깅 방법을 통해 도출된 값들을 식 (9)을 사용하여 Normalized Value로 적용하였다. 본 연구에서는 추력과 효율에 대해 동등하게 최대화시켜 적용하기 위해 b를 0.5의 값으로 하였다. 마이크로 유전 알고리즘을 통해 Table 4와 같이 새로운 변수 값들을 구하였다.
추력과 효율의 비중을 0.5로 동등하게 고려했을 때 추력의 값은 약 2.18로 최적화 기준 값인 1.533보다 높게 나왔지만 효율 값이 약 0.411로 기준 값 0.424보다 낮게 나왔다.
추력과 효율의 비중을 0.5로 동등하게 고려했을 때 추력의 값은 약 2.18로 최적화 기준 값인 1.533보다 높게 나왔지만 효율 값이 약 0.411로 기준 값 0.424보다 낮게 나왔다. 효율 값을 보완하기 위해 b를 0.6으로 보정하여 최적화를 다시 수행하였다. 고려한 b값으로 다시 최적화를 수행하였고 그 결과 값을 Table 5에 나타내었다. 추력 값은 b가 0.5일 때 보다 낮은 값이지만 앞서 기준 값 보다는 높으며 효율 또한 기준 값인 0.424보다 높은 값을 나타내었다.
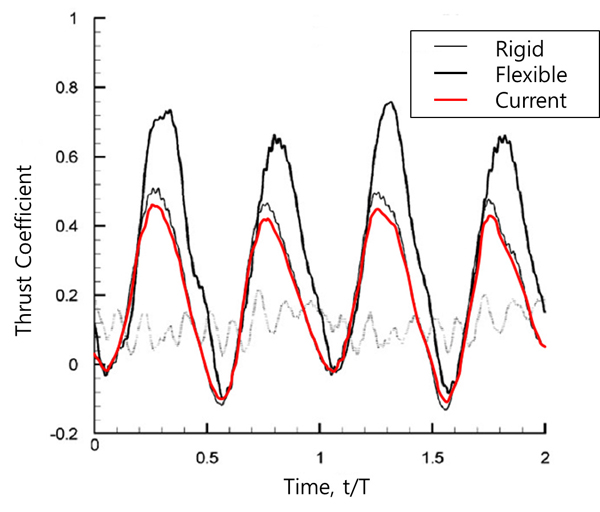
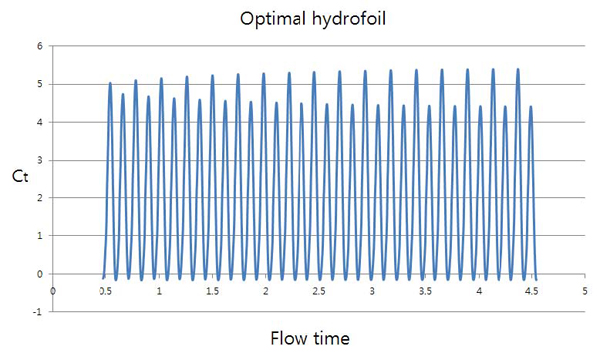
마이크로 유전 알고리즘을 통해 얻은 결과 값을 바탕으로 ANSYS Fluent를 이용해 확인실험을 하였다. Fig 8은 b값 0.6일 때의 추력 그래프를 나타낸 것이다. 불안정한 첫 번째 주기를 제외하고 나타냈다.
그림에서 볼 수 있듯이 두 번째 주기부터는 고른 형태의 추력 값을 나타내고 있고 주기적인 운동임을 확인할 수 있고 이는 안정적인 자율 무인 잠수정의 운동이 가능함을 나타낸다.
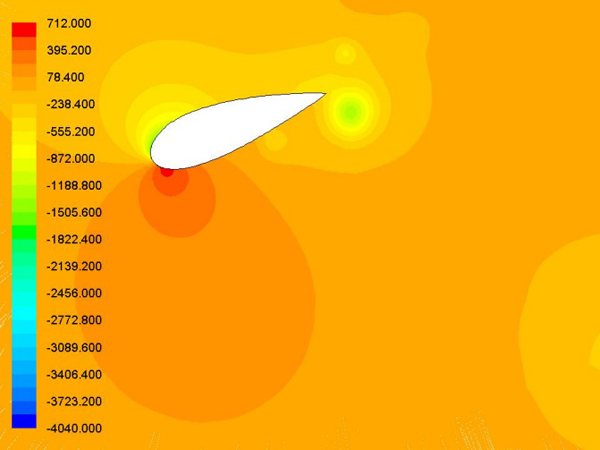
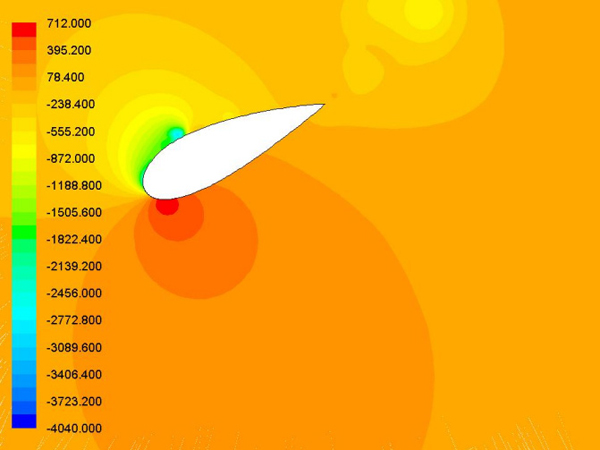
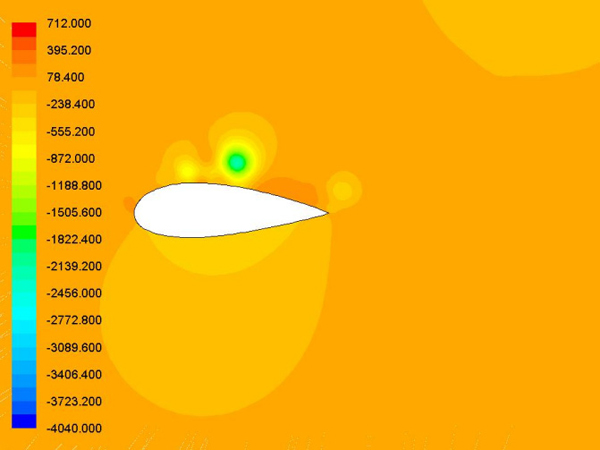
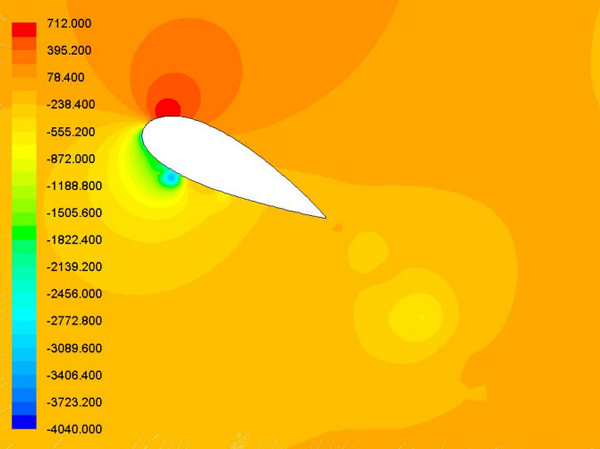
Fig 12에서 Fig 17는 알고리즘을 통한 결과인 새로운 에어포일 주변의 압력분포를 나타낸 것이며 이를 통해 Vortex(이하 와류) 및 움직임을 통한 생성되는 힘에 대한 상호작용을 알 수 있었다.
에어포일의 운동에 따라서 발생된 와류는 에어포일 윗면과 아랫면의 압력 차이에 따라 공력특성인 추력계수와 양력계수에 많은 영향을 준다. 에어포일의 움직임이 다운 스트로크 일 때, Fig 13, 14와 같이 에어포일의 아랫면의 압력은 높아지고, 윗면은 저압으로 변하여 양력과 추진력을 발생시켰다.
또한 업 스트로크의 경우에는 윗면의 압력이 높아지고 아랫면이 낮아지게 되어 음의 양력과 추진력이 발생된다. Fig 13에서 볼 수 있듯이 t/T=0.15가 지나면서 Leading Edge Vortex(LEV, 이하 앞전 와류)가 생성되고 에어포일의 윗면에서 머물러 있다가 t/T=0.62에 Trailing Edge Vortex (TEV, 이하 뒷전와류)의 형태로 빠져나가게 된다.
업 스트로크의 운동이 시작되는 t/T=0.5에도 와류는 앞전에서 뒷전으로의 이동이 있지만 계속적으로 윗면에서 작용을 하고 있으므로 뒷전 와류로 빠져나갈 때까지 음의 양력을 감소시키게 된다. 하지만 t/T=0.65부터 에어포일 아랫면의 앞전에서 와류가 다시 생성되고 다음주기가 시작되는 시점에서 와류가 빠져나갈 때까지 공력특성을 감소시키는 영향을 미치는 것과 유사하게 수중에서도 유사한 특징을 보였다. 따라서 한 주기 동안에 발생하는 와류의 영향을 고려하면 에어포일의 윗면에서 생성되는 와류가 영향을 주는 시간에 비해 아랫면에서 생성된 와류가 영향을 주는 시간이 더 크므로 플래핑 운동을 한 주기 하는 동안 발생된 와류는 플래핑 운동의 효율, 즉 실제 자율 무인 잠수정 움직임에 있어서 높은 효율을 가질 수 있다고 확인할 수 있었다.
5. 결 론
본 연구에서는 생체 유기적인 운동을 자율 무인 잠수정에 적용하기 위해 초소형 비행체에서 적용되는 플래핑 운동을 자율 무인 잠수정에 접목, 이에 맞는 플런징과 피칭의 조합인 운동을 사용하였고 최적의 추력을 갖는 형상과 효율을 갖는 설계를 하기 위해 최적화 기법을 적용하였다. NACA 4 digit 에어포일을 이용하여 2차원 유동 해석을 수행하였고 그 결과를 가지고 크리깅 방법을 통해 근사모델을 만들었다. 형상과 운동을 최적화하기 위해 마이크로 유전 알고리즘을 적용하였다.
마이크로 유전 알고리즘을 통해 나온 결과로 최대 캠버 2.993, 최대 캠버의 위치 2.341, 두께 28.187, 플런징 높이 0.797, 피칭 각도 23.120, 위상각 87.984의 추력과 효율에서 최적의 값을 낼 수 있는 형상과 운동을 찾을 수 있었다. 이 결과는 실제 자율 무인 잠수정의 실험값보다 추력은 약 27%, 효율은 4.7%정도 향상시켰다.
이는 형상과 운동을 동시에 고려한 결과이며 최적의 추력과 효율을 발생 시킬 수 있는 최적의 값이다.
Cavitation이 발생하는 경우 AUV의 성능특성에 직접적인 영향이 미칠 수 있으므로 설계초기단계에서 주어진 유동장에 대하여 각 난류모델의 수치해석을 통하여 문제에 적합한 수치해석모델을 이용하여 Cavitation 발생유무를 확인하는 것이 필요하다.
더하여 차후 3차원 Combined motion에 대한 해석 연구와 실제 지느러미에 가까운 형상을 적용하여 더 나은 추력과 효율을 얻는 연구가 필요하다고 생각된다.
Acknowledgments
이 논문은 교육과학기술부 첨단 사이언스. 교육 허브 개발 사업(2011-0020562)지원 및 국방과학연구소(과제번호 ADD- 12-01-08-13, Wavelets을 이용한 고속 비행체 공력해석 및 대용량 데이터 베이스 관리 기술 개발)의 기초 연구비 지원에 의한 연구 결과입니다.
References
- D. Richard. Blidberg, “The Development of Autonomous Underwater Vehicles (AUV); A Brief Summary”, Autonomous Undersea Systems Institute.
- Jeffrey A. Walker, Mark W. Westneat, “Integrative & Comparative Biology”, OXFORD Journal, (2002), 42, p1032-1043.
-
M. A. Ashraf, J. Young, J. C. S. Lai, “Reynolds number, thickness and camber effects on flapping airfoil propulsion”, Journal of Fluids and structures, (2011), 27, p145-160.
[https://doi.org/10.1016/j.jfluidstructs.2010.11.010]

-
Ismail H. Tuncer, Mustafa Kaya, “Optimization of flapping airfoils for maximum thrust and propulsive efficiency”, AIAA Journal, (2005), 43, p2329-2336.
[https://doi.org/10.2514/1.816]

-
Stephen. Licht, Victor. Polidoro, Melissa Flores, Franz S. Hover, Associate member, IEEE, and Michael S. Triantafyllou, “Design and projected performance of a flapping foil AUV”, IEEE Journal of oceanic engineering, (2004), 29, p786-794.
[https://doi.org/10.1109/JOE.2004.833126]

-
Alexandra H. Techet, “Propulsive performance of biologically inspired flapping foils at high Reynolds numbers”, The Journal of Experimental biology, (2008), 211, p274-279.
[https://doi.org/10.1242/jeb.012849]

- M. A. Ashraf, J. C. S. Lai, J. Young, “Numerical Analysis of flapping wing aerodynamics”, 16th Australasian Fluid Mechanics Conference, (2007), p1283-1290.
- Wilkins, P., Knowles, L., “Investigation of aerodynamics relevant to flapping-wing Micro Air Vehicles”, AIAA paper 2007-433, (2007.).
-
S. Heathcore, Z. Wang, I. Gursul, “Effect of spanwise flexibility on flapping wing propulsion”, Journal of Fluids and Structures 24, (2008), p183-199.
[https://doi.org/10.1016/j.jfluidstructs.2007.08.003]

-
Joel E. Guerrero, “Effect of Cambering on the Aerodynamic Performance of Heaving Airfoils”, Journal of Bionic Engineering, (2009), 6, p398-407.
[https://doi.org/10.1016/S1672-6529(08)60134-1]

- 한표경, 김동욱, 이종수, “구속조건의 가용성을 고려한 크리깅 메타모델 및 반응 표면 기반의 순차적 근사최적화 방법”, 대한기계학회 추계학술대회 강연 및 논문 초록집, (2007), p267-277.
- Framax Co. Ltd, “P.I.A.N.O. Manual V2.1.”, (2008.).