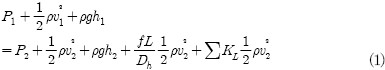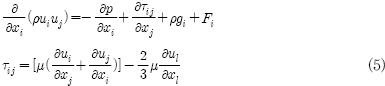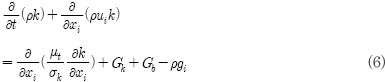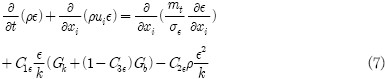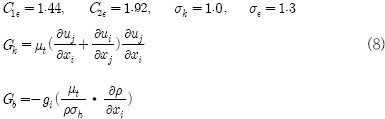The Effect of Divergence Angle on the Control Valve Trim Characteristics

1. 서 론

고차압 밸브는 과도하게 높은 압력강하에서도 동작할 수 있도록 설계된다. 압력 강하로 인해 생성된 유체의 높은 운동에너지는 공동화 현상(cavitation), 플래싱(flashing), 질식유동(choked flow), 소음 및 진동과 같은 문제를 발생시킨다. 이로 인해 밸브의 주요 부품인 트림(trim), 디스크(disk), 씨트링(seat-ring), 플러그(plug)등에 손상을 유발한다. 그러므로 이상적인 압력강하는 밸브의 트림에 적은 에너지를 흡수시키고 과도한 유속을 발생시키지 않도록 설계되어야 한다.(1)

공동화 현상은 밸브 내의 국부적인 높은 속도로 인한 낮은 압력 영역에 의해 발생되는데, 일반적으로 씨트(Seat) 지역이나 밸브 개구부(vena contracta), 하류부(down-stream)와 같은 대상 지역에서 발생하게 된다. 이와 같은 문제점들을 해결하기 위해서 선진국에서는 1980년대 초부터 유로 면적의 변화 없이 압력 손실을 유도하는 미로형 밸브(labyrinth type valve)를 연구하였으며, Rahmeyer 등(2)은 구불구불한 형태의 트림유로가 공동화 현상을 감소시키는데 효과적임을 실험으로 입증하였다. 현재 밸브 내의 공동화 현상 방지를 위한 미로형 밸브들은 CCI, FISHER, JVS Engineers, Copes-Vulcan 등의 주요 밸브 제작업체에서 제품화되어 있다.(3)

국내에서는 1990년 초부터 미로형 밸브의 수요와 더불어 연구가 활발히 진행되어왔다. 권갑주 등(3)은 3방향(120°간격) 5단의 구조로 되어진 헬리컬 트림(helical trim)을 개발하여 유체의 공동화 현상과 소음을 개선하였다. 또한 박은희 등(5)은 멀티홀 2단(multi-hole two stage)을 사용한 가변오리피스를 이용하여 밸브의 안전성을 확보하였다. 이와 같은 선행 연구들은 주로 다단(multi-stage)에 대해 진행된 반면, 김대권 등(6)은 밸브 트림의 끝단 형상을 반경방향으로 변화시킴으로써 공동화 현상이 억제됨을 확인하였다. 그리고 공동화 현상의 발생 유무를 예측하기 위해 정민호 등(7)은 유체해석 프로그램인 FLUENT를 이용하여 밸브 개도율(valve opening)의 변화에 따른 글로브 밸브의 3차원 유동장 해석과 압력 강하 및 유량계수를 실험값과 비교하는 연구를 수행하였다. 안영준 등(8)은 액체를 작동 유체로 다루는 LNG 선박용 고차압 밸브에 대해 상용 전산열유체 해석프로그램인 CFD-ACE를 이용하여 유동장을 해석하였다.

그러나 기존의 연구들은 주로 다단 미로형 밸브의 공동화 현상에 대해서만 이루어졌고 유로 형상 변화에 따른 유동 현상과 차압 증가에 대한 연구는 진행되지 않았다. 또한 미로형 밸브의 꺽임(turn)수가 증가하면 공동화 현상 억제효과는 크지만 전체 속도수두 손실 및 스택(stack)의 직경에 영향을 미치므로 꺽임(turn)수를 적절히 조절해야 한다. 디스크 스택의 증가는 밸브를 지나는 유량 특성과 성능에 영향을 미친다. 그러므로 고차압 밸브에서는 공동화 현상의 억제뿐만 아니라 한단의 차압을 크게 만드는 것도 중요하다.

본 연구에서는 단(stage)의 차압을 증가시키기 위해서 다단의 미로형 유로형상에 확산각을 적용하였으며 상용프로그램인 FLUENT를 이용하여 전산해석을 수행하였다. 이 결과를 통해 트림 성능을 평가하고자 한다. 기존의 확산각이 없는(0 °) 고차압 미로형 밸브 모델과 5가지의 확산각(20°, 30°, 40°, 50°, 60°)을 적용한 밸브를 비교해 각각 유동특성과 압력강하 및 손실계수 등을 분석하였다.

2. 이론적 배경

2.2 밸브 내 압력강하

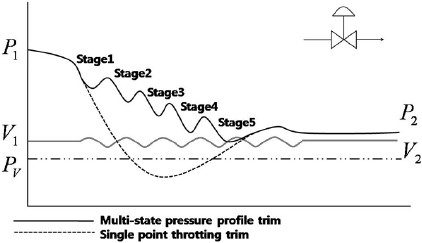
입ㆍ출구 압력과 속도 관계를 표현한 베르누이 방정식은 마찰 손실을 포함한 수정된 베르누이 방정식으로 식 (1)과 같이 쓸 수 있다.

Fig. 1

Design specifications of multi-stage trim

일반적인 관로는 내부의 마찰에 의한 주손실과 유동의 교란, 유동박리, 혼합 등으로 인한 부가적인 손실을 야기한다. 긴 파이프 시스템의 부가적인 손실은 주손실에 비해 작다. 하지만 경우에 따라 부가적인 손실이 주손실보다 큰 경우가 있다. 예를 들어 짧은 거리 안에 벤드와 밸브가 많은 파이프 가 여기에 속한다. 본 연구에서는 90°로 굽은 관의 거리가 매우 짧으므로 부가적인 손실만을 고려하였다. 관로의 부가적인 손실은 국부 유체저항에 의한 손실 (∑K_L×(pv²₂/2))이다. 압력손실계수(K_L)는 밸브 전후의 압력손실을 동압으로 나누어 구하며 식(2)로 표현된다.(10) 압력손실계수는 미로형 밸브의 설계에서 가장 많이 사용하는 무차원 변수이다.

손실계수(K_L)는 식 (3)과 같이 형상에 많은 영향을 받으며, 유체의 레이놀즈 수에도 또한 영향을 받는다.

하지만 난류일 경우 손실계수는 레이놀즈 수에 크게 영향을 받지 않고 형상에 지배적인 영향을 받게 된다.

3. 수치해석

3.2 해석 기법 검증

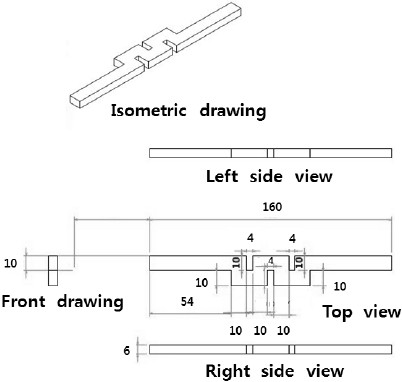
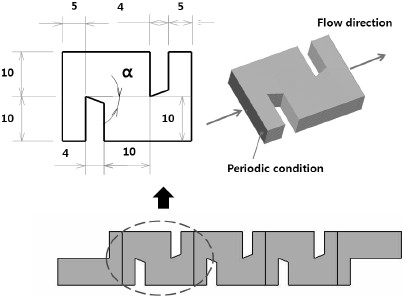
해석기법을 검증하기 위해 고차압 유량제어용 미로형 밸브의 하나의 통로에서 8번 꺾임(turn)있는 모델을 사용하였으며,(11) 형상은 Fig. 2와 같다. 밸브 입구의 수력직경(D_h)은 7.5 mm이며 밸브의 높이는 6 mm이다. 1 단(stage)가 10mm 등간격으로 배치된 다단 회전(Multiple turn) 미로형 밸브이다.

이 실험에서는 미로형 밸브의 손실계수 측정을 위해 유량계와 압력계를 이용하여 미로형 밸브 내의 손실계수를 측정하였다. 배관 시스템은 미로 모델과, 펌프, 유량계, 압력계를 포함하고 있으며 레이놀즈 수를 변화시키면서 실험이 수행되었다. 또한 실험에 사용된 작동유체는 50℃, 60℃인 물을 이용하였다.

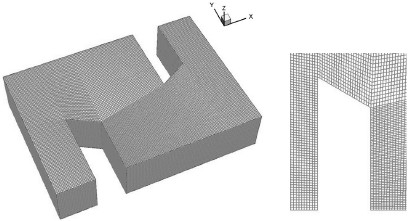
해석을 수행하기 위한 격자생성은 Gambit 2.4.6을 사용하였으며, 계산의 정확도를 높이기 위하여 정렬격자를 생성하였다. 본 연구에서는 미로형 밸브의 내부 유동장에 대해 비압축성 3차원으로 가정하였으며 사용전산 유체역학 코드는 FLUENT 6.3.26을 사용하였다. 연속방정식과 운동량방정식의 조합에는 SIMPLE (Semi-implicit mehtod for pressure linked equation) 해법을 사용하였으며 운동량과 공간차분에는 2차 풍상차분법(upwind method)를 사용하였다. 본 연구에서는 15℃인 물을 3차원 정상상태의 비압축성 유동이라 가정하였으며 난류모델을 적용하여 해석을 수행하였다. 계산 조건은 Table 1과 같이 유량을 3 l/min에서 16 l/min까지 변화시켜가며 계산하였다.

Table 1.

CFD condition for validation model

Fig. 2

Experimental model with 8 turn single passage, dimensions in millimeters(11)

Fig. 3

Experimental result of Re-Δp in 8 turn single passage

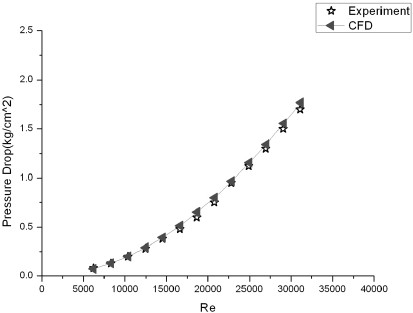
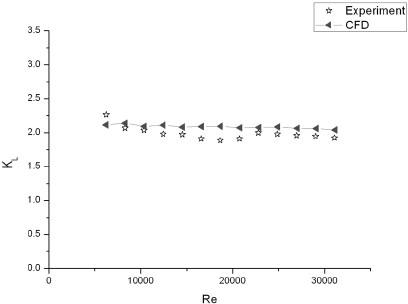
Fig. 3은 레이놀즈 수에 따른 실험과 전산해석의 결과를 비교한 그래프이다. 레이놀즈 수가 증가할수록 밸브 내의 차압도 함께 증가함을 알 수가 있으며 해석과 실험의 결과가 서로 유사함을 확인 할 수 있다.

Fig. 4는 레이놀즈 수에 따른 손실계수의 실험 결과와 전산해석의 결과를 비교한 그래프이다. 유량에 따른 차압과 손실계수(K_L)를 나타낸 실험 결과에서 보여주듯 레이놀즈 수가 15,000이하에서 레이놀즈 수에 따라 손실계수가 조금씩 감소하는 경향을 보인다. 그러나 그 이상의 레이놀즈 수에서는 거의 일정한 손실계수 값을 나타내고 있다. 전산해석의 결과는 전영역에서 일정한 손실계수 값을 가지며 레이놀즈수 전영역 내에서 실험과 전산해석 결과가 유사함을 확인할 수 있었다.

Fig. 4

Experimental result of Re-KT in 8 turn single passage

3.3 확산각에 따른 유동해석

확산각에 따른 영향을 살펴보기 위해 고차압 유량제어용 미로형 밸브의 하나의 통로는 8번 꺽임(turn)있는 모델을 사용하였고 내벽 형상은 0°에서부터 60°까지의 확산각을 적용하여 한 단에서의 압력강하량과 유동 현상을 알아보았다. Fig. 5는 해석에 사용된 확산각이 있는 미로형 밸브 한 단의 3차원 모델을 나타낸 것이다. Fig. 5의 형상은 원칙적으로 주기조건을 줄 수 있는 현상이 아니지만, 다단으로 밸브를 제작하는 경우에는 Fig. 5와 같이 계산형상이 반복되므로 주기조건을 주어 수치계산을 하였다.

해석을 수행하기 위한 작동유체는 비압축성 물을 사용하였으며 원전용 미로형 밸브의 작동 조건인 레이놀즈 수(18,000/ 28,000/ 38,000) 영역에서 계산을 수행하였다. Fig. 6은 한 단내의 유동 해석을 위해 생성한 3차원 격자계를 보여주고 있다. 또한 확산각 6가지 모델(0° /20° /30° /40° /50° /60°)에 대한 계산격자는 약 200,000개로 구성하였다. 모든 벽면은 no-slip 조건을 적용하였으며, 입출구는 주기(Periodic) 조건을 이용하였다. 다단 트림의 압력강하선도는 한 단에서의 압력강하가 연속적으로 일어나는 형태를 보인다. 따라서 각 단을 지나는 유체의 압력강하는 유로의 진행 방향으로 일정한 차압을 발생하게 된다. 본 연구에서는 한 단에서의 차압과 유량 조건을 상용전산해석 코드인 Fluent의 주기조건으로 사용하였다. 유동의 유입 부분은 mass flow inlet (0.28/0.42/0.56)조건으로 설정하였다. 난류 영역에서 작동하는 미로형 밸브 내의 유동을 모사하기 위해 표준 k-ε model을 사용하였으며 벽 근처영역에서는 첫 번째 격자점까지의 거리(Y⁺)를 50에서 100으로 분포시켰다.

Fig. 5

Analysis model with 1 stage passage using the divergence angle, dimensions in millimeters

Fig. 6

Computational grids of the 1 stage passage

4. 계산결과 및 고찰

본 연구에서는 고차압 밸브에 사용되는 미로형 밸브 내의 유동 분포와 압력강하 및 속도 분포를 확인하고 미로형 밸브내에서 확산각의 영향을 확인하기 위하여 수치해석의 결과들을 서로 비교하였다.

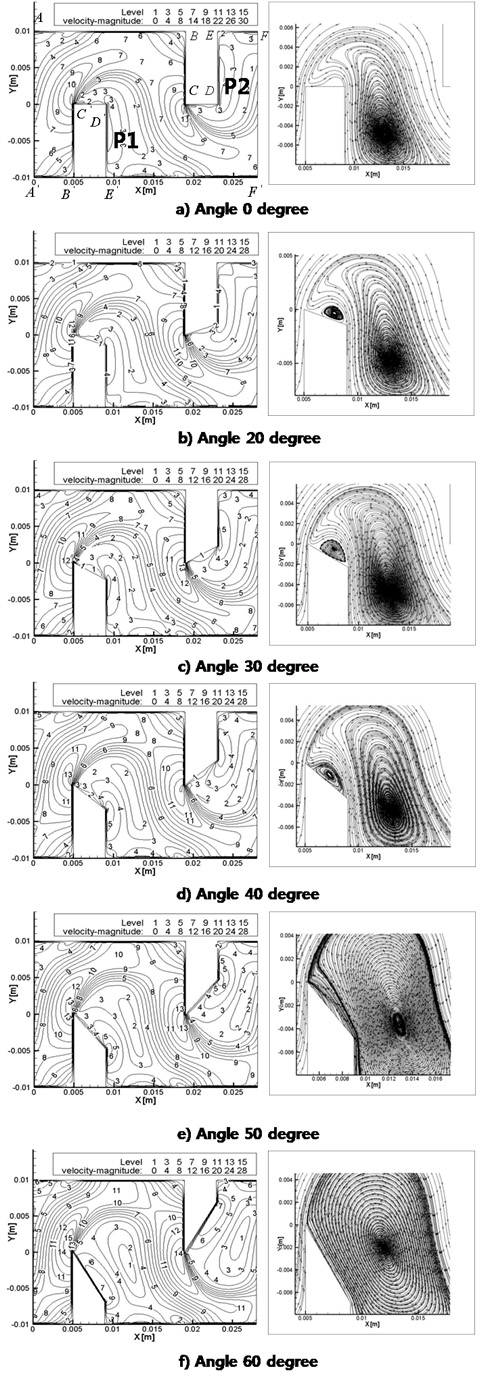
Fig. 7의 좌측은 레이놀즈 수 28,000 영역에서 한 단내의 속도크기를 나타낸 것이며 Fig. 7의 우측은 한 단내의 속도벡터를 XY평면에 나타낸 것이다. Fig. 7(a)은 확산각이 0°인 경우에 대한 결과로서, 미로형 유로 모양을 따라 흐르는 유속 크기는 Fig. 7(a)의 좌측에서 관찰할 수 있다. 이때 C'와 C지점에서 발생하는 유동 박리로 인해 내벽 C'-D와 C-D후방에 큰 재순환 유동이 관찰됨을 우측 그림에서 볼 수 있다. 이로 인해 유로 면적이 줄어들면서 주유동의 속도는 증가하게 된다. 최대 속도는 C'와 C 지점 부근에서 관찰되는데 확산각이 0° 인 경우 22m/s 정도의 값을 보인다.

확산각이 20° 인 경우에 대한 결과를 보면 주 재순환 유동의 영역이 더 커지면서 최대속도는 조금 더 큰 값을 나타낸다. 재순환 유동영역의 증가와 최대속도의 증가는 모두 미로형 밸브 내의 에너지 손실을 증가시키므로 더 큰 압력손실을 야기한다. 그리고 D'와 D점에서 주유동의 역류로 인해 2차 재순환 유동이 발생함을 Fig. 7(c)의 좌측에서 확인할 수 있다.

확산각이 30° 인 경우에 대한 결과를 보면 확산각이 커짐에 따른 주 재순환 영역의 유속이 더 커지면서 내벽 D'-E'를 지나게 된다. 내벽 D' 지점의 가속된 유체로 인해 내벽 C'-D'의 2차 재순환 영역이 더욱 확대됨을 Fig. 7(c)의 우측에서 볼 수 있다. 확산각이 40° 인 경우에 대한 결과를 보면 확산각의 증가에 따른 유로내 유속은 더욱 증가하였으며 내벽D'-E' 근방의 유속 증가와 경사진 벽면으로 인해 벽면 C'-D' 근방의 2차 재순환 영역은 사라짐을 Fig. 7(d)의 우측에서 볼 수 있다.

Fig. 7

Velocity Magnitude contour(Left) and streamlines near the wall (Right) with divergence angle for Re 28,000

Fig. 8

Sections in curved duct without divergence angle for Re 28,000

확산각 50°, 60°인 경우에서는 급격한 경사로 인해 벽면 C'-D' 근방의 2차 재순환 영역이 사라지고 재순환 영역(P1)이 내벽 C'-D' 표면을 따라 크게 생성됨을 Fig. 7(e)와 (f)의 우측에서 확인할 수 있다. 또한 내벽 C'-D'를 지나는 유속은 확산각 50°에 비해 확산각 60°에서 더 큰 값을 보이며 주 재순환 영역 P1의 중심을 지나는 유체의 유속은 감소함을 확인 할 수 있다. 또한 확산각 50°, 60°의 속도크기를 나타내는 좌측 그림을 보면 유속의 크기는 확산각이 없는 경우에 비해 외벽 A-B 방향으로 큰 유속 크기를 가지게 된다. 확산각이 60°의 굽은 관은 벽면 B'와 C 지점에서 가장 큰 유속을 관찰되는데 그 값은 28m/s 정도를 갖는다.

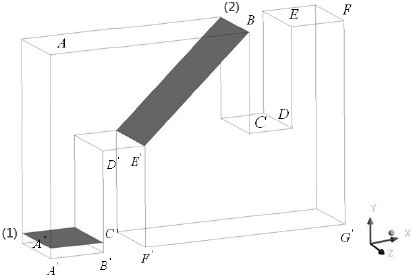
한 단내에서 유동에 수직한 속도 성분인 2차 유동을 확인하기 위해 Fig. 8의 단면 (1)과 (2)를 선정하였다.

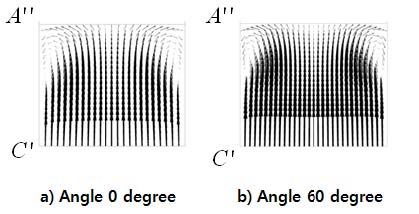
Fig. 9는 단면 (1)에서 유체의 2차 유동에 대한 벡터를 나타낸 것이다. Fig. 9(a)는 레이놀즈 수 28,000 영역에서 확산각이 0°인 경우에 대한 결과로서, Fig. 8의 A'' 부근에 약한 2차 유동이 발생하며 이러한 2차유동은 휘어지는 유동에서 흔히 발견되는 현상이다.(12) Fig. 9(b)는 레이놀즈 수 28,000 영역에서 확산각이 60°인 경우에 대한 결과로서, (a)경우보다 2차유동이 커진것을 알 수 있다. 즉, 확산각이 커짐에 따라 2차 유동에 대한 손실이 증가하는 것을 확인할 수 있다.

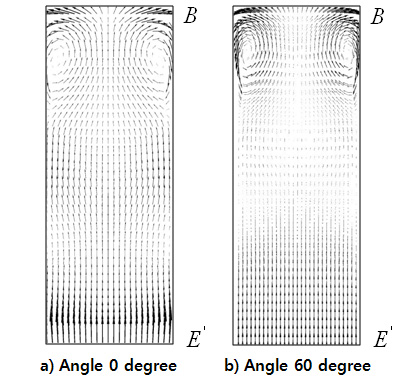
Fig. 10(a)은 단면 (2)에서 확산각이 0°인 경우에 대한 결과로서, B 부근에 약한 2차 유동이 발생하는 것을 확인할 수 있다. 이러한 2차 유동은 확산각이 60°인 경우에서 그 크기가 더욱 증가함을 알 수 있다.

Fig. 11은 한 단내의 난류 에너지 생성항(turbulence energy production)에 대한 분포를 XY 평면에 나타낸것이다. 관내의 유동은 벽면에서의 충돌과 급격한 방향 전환으로 인하여 강한 대칭형의 2차 유동이 발생하며 이는 레이놀즈 응력에 의해 강한 대류 및 유동 편중을 유발시켜 매우 복잡한 유동현상이 나타난다.(13) 난류 에너지 생성항은 이러한 복잡한 90° 관내의 유동에서 손실이 발생하는 지점을 보여줄 수 있다. 난류에너지 생성항이 큰 경우 유동손실이 큰 것으로 알려져 있다.(14)(15)

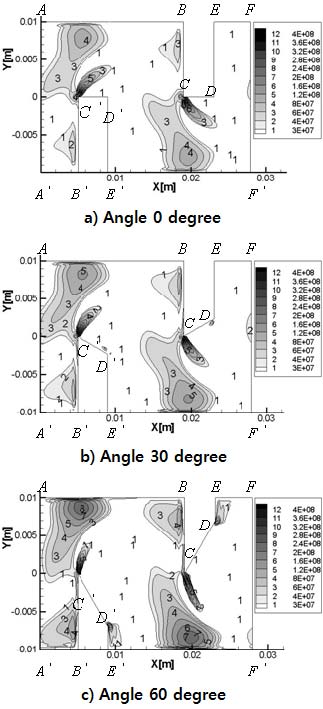
Fig. 11(a)은 레이놀즈 수 28,000 영역에서 확산각이 0°에서의 난류 에너지 생성항 분포를 유동방향에 따라 나타낸 그림이다. 난류에너지 생성항이 가장 큰 영역은 C와 C'지점 부근에서 관찰된다. 이 지점은 최대속도가 발생하는 위치와 가까우며 바로 옆에 위치한 재순환 영역에 강한 전단류가 형성되는 영역이다. 그리고 주유동이 벽면에 충돌하면서 급격한 방향전환을 하는 영역으로써 벽면 A-B와 A'-B' 주위에서 난류에너지 생성항은 발견된다. C ‘-B '와 C-B 주위의 유동은 벽면에 충돌하면서 유동이 급격한 방향전환을 하는 영역이며 이 영역에서 큰 난류 에너지 생성항을 확인할 수 있다. Fig. 11(b)는 레이놀즈 수 28,000 영역에서 확산각이 30°의 결과를 나타내고 있다. 이 그림에서 보면 확산각이 커지면서 C '와 C 지점 주위 영역의 난류에너지 생성항 크기가 감소한다. 그러나 주유동이 A-B와 B-C 벽면 주위 영역의 벽면에 충돌하게 되고 이로 인해 급격한 방향전환을 하면서 발생하는 큰 난류 에너지 생성항은 확산각이 커지면서 더욱 강해지는 것을 알 수 있다. Fig. 11(c)는 레이놀즈 수 28,000 영역에서 확산각 60°의 난류 에너지 생성항 분포를 나타낸 그림이다. 확산각이 커지면서 A-B와 B-C 벽면 주위에서 난류 생성항이 더욱 커지는 것을 확인할 수 있다. 그리고 D-E 주위의 난류 생성항이 상당히 커진 것을 알 수 있다.

Fig. 9

Secondary flow vector diagram for section (1) for Re 28,000

Fig. 10

Secondary flow vector diagram for section (2) for Re 28,000

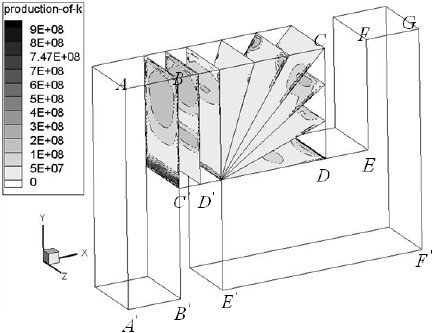
Fig. 12는 레이놀즈 수 28,000 영역에서 한 단내의 난류 운동 에너지 생성 분포를 유동방향에 수직한 단면에 나타낸것이다. 관내를 흐르는 유체가 내벽 B'C'을 지나면서 강한 회전운동을 발생시키고 이는 레이놀즈 응력 증가로 인한 난류 생성을 증가시켜 난류 에너지 생성을 증가함을 내벽 C' 지점을 통해 확인할 수 있다. 가속된 유체가 외벽 AB의 벽면을 따라 흐르면서 유체의 마찰을 유발하며 이는 난류강도를 증가시켜 난류 에너지 생성을 증가시킴을 외벽 B에서 알 수 있다. 대칭적인 측벽 주위에 난류운동에너지 생성항이 크게 나타난 것은 2차 유동에 의해 발생하는 것으로 판단된다.

Fig. 11

Contour of turbulence energy production for Re 28,000

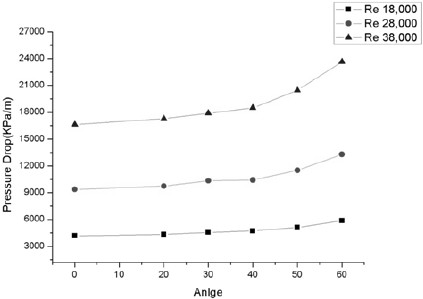
Fig. 13은 레이놀즈 수에 따른 미로형 밸브 한 단에서의 확산각과 압력강하의 영향을 나타낸 것이다. 레이놀즈 수가 증가할수록 압력강하량이 커짐을 알 수 있다. 확산각에 따른 압력강하는 40°까지 비교적 완만하게 증가하다가 확산각 50°, 60°에서 급격하게 증감함을 확인할 수가 있었다. 이는 레이놀즈 수가 커짐에 따라 미로형 밸브를 지나는 유체는 유속을 증가시키고 더 많은 유체마찰을 발생하여 한 단에서의 차압이 증가한 것으로 보인다.

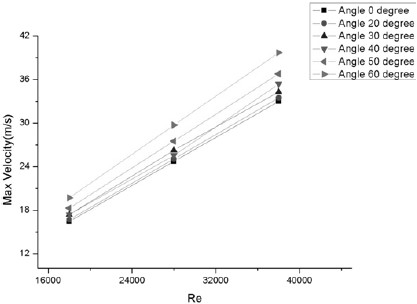
Fig. 14은 미로형 밸브 한 단에서의 레이놀즈 수와 확산각에 따른 최대유속을 나타낸 것이다. 입구 유량 조건은 0.28kg, 0.42kg 및 0.56kg으로 변화시켜가며 수치해석을 수행하였다. 레이놀즈 수가 증가할수록 확산각 형상 부근에 나타나는 최대유속 또한 함께 증가함을 볼 수가 있다. 레이놀즈 수 18,000과 38,000 사이의 최대 유속 차이는 확산각이 없는 경우 보다 확산각 60°의 경우에서 크게 나타남을 확인 할 수가 있었다. 따라서 높은 레이놀즈 수에서는 확산각이 커짐에 따라 급속한 유속 증가를 야기한다. 본 연구에서는 급격한 속도변화에 의한 공동화 현상을 확인하기 위해 공동화 지표(Cavitation indices)를 사용하였다. 공동화 지표(σ)는 공동화를 촉진하는 힘과 공동화에 대항하는 힘의 비로서 나타낸다. 이 값이 클수록 밸브 내에서 공동화 손상이 발생할 확률이 작아진다. 본 연구에서의 한 단내의 공동화 지표는 6에서 10사이로 Valtek International(9)에서 제공하는 초기 공동화 지표인 0.3∼0.001을 만족하므로 한 단내의 공동화 현상에 대한 가능성을 배제하였다.

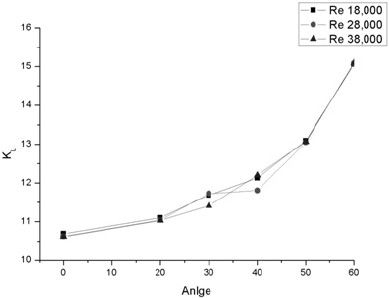
Fig. 15에서는 확산각을 가진 미로형 밸브 한 단에 대한 손실계수선도를 나타내었다. 본 연구에서는 손실계수의 계산에 사용된 속도(υ)를 입구 평균 속도로 적용하였다.

확산각을 가진 경우와 그렇지 않은 두 경우 모두가 레이놀즈 수에 큰 영향 없이 손실계수가 증가함을 확인할 수가 있었다.

Fig. 12

Production of turbulent kinetic energy for Re 28,000

Fig. 13

Relation of pressure gradient and angle with Reynolds numbers

Fig. 14

Relation of maximum velocity and angle with Reynolds numbers

Fig. 15

Relation of divergence angle and local flow resistance with Reynolds numbers

5. 결 론

본 연구에서는 확산각을 가진 미로형 밸브 한 단의 관 내부를 흐르는 유동장에 0°, 20°, 30°, 40°, 50°, 60° 의 6가지의 확산각을 적용하여 전산해석을 수행한 후 연속적으로 90° 로 꺾이는 미로형 밸브의 유체역학적 데이터를 확보하였으며 다음과 같은 결론을 얻었다.

[1] 확산각이 증가함에 따라 박리유동 영역이 커지면서 압력손실이 커짐을 확인할 수 있다.

[2] 확산각이 증가함에 따라 박리유동영역이 커지면서 주유동의 속도가 증가하게 된다. 이로 인해 주유동이 벽면에 충돌하고 방향을 전환하는 정도가 커지면서 압력손실을 증가시키게 된다.

[3] 확산각이 증가함에 따라 미로형 밸브 내의 2차유동이 증가하게 되고 이로 인해 유체의 손실이 증가함을 난류 생성항 분포에서 확인할 수 있었다.

[4] 국부유체손실계수는 관내의 형상과 레이놀즈 수에 지배적인 영향을 받으며 확산각이 증가할수록 관내의 박리유동과 재순환 유동으로 인해 난류의 생성과 유체와 벽면 간의 마찰을 증가시켜 유체의 내부 에너지가 증가시키게 된다. 이러한 유체의 에너지 손실은 유체의 압력강하를 증가시키게 된다.

Acknowledgments

본 연구는 2010년도 지식경제부의 재원으로 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 결과입니다 (No. 20104010100540).

References

• G. Borden, P.G. Friedmann, “Practical guides for measurement and control”, ISA, (1998.).
• W.J. Rameyer, H.L. Miller, S.V. Sherikar, “Cavitation Testing Result for a Tortuous Path Control Valve”, ASME, FED, (1995), 210, p62-66.
• 김재웅, “해양플랜트용 고압ㆍ고차압 제어밸브의 구조 안전성 평가”, 한국생산제조시스템학회지, (2011), 20(5), p553-558.
• 이덕구, 김영범, 윤인식, 황지혁, 권갑주, “원자력 밸브용 헬리컬트림의 유동 타입에 따른 특성”, 대한기계학회 춘계학술대회 논문집, (2007), p3211-3216.
• 박은희, 이현우, 최성철, 정경훈, “압력 강하가 밸브 Trim 특성에 미치는 영향”, 한국자동차공회 추계학술대회 논문집, (2003), p167-174.
• 김대권, 손채훈, “고차압 글로브 밸브 트림의 anticavitation에 관한 수치적 연구”, 대한기계학회 추계학술대회 논문집, (2010), p3000-3003.
• 정민호, 양상민, 이호영, “공기구동형 글로브 밸브의 3차원 유동해석”, 유체기계저널, (2005), 8(4), p7-13.
• 안영준, 김병진, 신병록, “Cavitation Trim을 갖는 고차압 제어밸브의 유동특성에 관한 수치해석”, 유체기계저널, (2007), 10(4), p61-70.
• P.L. Skousen, “valve handbook”, second edition, McGraw-Hill, (2006).
• Y.A. Cengel, John M. Cimbala, “Fluid Mechanics Fundamentals and Applications”, McGraw-Hill, (2010).
• 김기철, 허진호, 박재서, 이준우, 강범수, 김귀순, 김정, 정기호, 송기범, 하병국, “원자력 발전소 고차압 유량제어용 미로형 밸브 설계 및 양산”, 과학기술부, (2000).
• 맹주성, 이종신, “사각다면을 갖는 90° 급곡관의 3차원 난류유동 해석”, 대한설비공학회 설비공학논문집, (1991), p11-25.
• 김신, 김영범, 편저, “난류 입문”, 대영사, (2001).
• A Duncan. Walker, F Jonathan. Carrotte, Andrew M. Rolt, “Duct aerodynamics for intercooled aero gas turbines”, proceedings of ASME Turbo Expo 2009: Power for Land, Sea and Air(GT2009-59612), (2009).
• Masafumi Hirota, Hajime Yokosawa, Hideomi Fujita, “Turbulence kinetic energy in turbulent flows through square ducts with rib-roughened walls”, Heat and fluid flow, (1992), 13(1), p22-29. [https://doi.org/10.1016/0142-727X(92)90056-F]