A Numerical Analysis on Mixing Performance for Various Types of Turbine Impeller in a Stirred Vessel
In the present study, a numerical simulation to analyze mixing performance inside an industrial mixer was investigated for various geometry of turbine impellers. Various pitching angles and various types of turbine blades were considered in the simulation. In order to model the rotation of impeller, the Multiple Reference Frames (MRF) technique was used. For evaluation of the effect of various shapes on the mixing performance, dimensionless coefficient such as flow coefficient, circulation coefficient, power coefficient, pumping effectiveness and circulation effectiveness were used. From the results, the effect of pitching angle of a pitched turbine impeller was to give best pumping effectiveness around 30º pitching angle, whereas best circulation effectiveness around 65º pitching angle. Dual pitched turbine impeller showed best performance in both pumping effectiveness and circulation effectiveness among impeller types considered in the present study.
Keywords:
Mixers, Mixing Performance, Turbine Impeller, Computational Fluid Dynamics, Multiple Reference Frames, 교반기, 교반성능, 터빈 임펠러, 전산유체 역학, 다중 좌표계1. 서 론
전통적으로 교반기는 단일 또는 다상의 물질을 고루 섞어주기 위해 사용되는 기계로서 주로 식품, 생화학, 금속, 수 처리 등 산업 전반에 널리 사용된다. 이러한 교반기는 용도나 기능에 따라 내부의 혼합현상이 매우 다양하게 일어나기 때문에 임펠러나 교반 용기 등의 내부 형상과 작동 조건을 고려하여 설계되어야 한다. 사용 환경에 따라 최적의 교반성능을 내기 위해서는 교반기 내부의 유동특성 및 이에 따른 교반결과에 대한 분석이 이루어져야 한다. 최근 컴퓨터의 발달과 함께 수치해석의 해석 신뢰성이 높아지면서, 교반기 연구에 대하여 수치해석적인 방법은 실험과 경험에 의한 방법의 대안이 되고 있다. 이러한 수치해석 방법은 해석 결과를 시간과 공간에 따라 분석할 수 있는 장점을 가지고 있기 때문에 최근 교반기 연구에 많이 이용되고 있다.
교반기에 대한 이러한 수치해석적 연구로, 김치겸 등(1)은 비정상 상태에서 배플의 형상에 따라 고체와 액체의 교반에 대한 연구를 진행하였다. 교반기 내 고체입자 분포를 확인하였으며 배플의 수가 교반 시간과 유동 특징에 미치는 영향에 대해 분석하였다. 장재원과 허남건(2)은 45° pitched paddle이 설치된 교반기 내 유동을 임펠러의 설치위치와 토크 변화에 따라 수치해석을 수행하였고, 임펠러 설치위치를 제안하였다. Kumaresan과 Joshi(3)는 레이저도플러속도계를 이용한 실험적인 방법과 수치해석을 이용한 방법으로 임펠러의 형상 및 교반 동력에 따라 교반기 내 유동형태를 연구하였고, 실험과 수치해석에서 모두 블레이드의 피치에 따라 유동계수와 동력계수의 관계를 확인하였다. Nienow(4)의 교반기 형상에 따른 연구에서 교반기 크기에 대한 임펠러의 크기의 비가 증가할수록 더 효과적인 교반 성능과 적은 교반시간이 나타난다는 결과와 임펠러가 클수록 토출유량이 증가하며 이는 유동계수와 혼합의 균일함을 증가시킨다는 결과를 확인하였다. Garcia 등(5)은 네 개의 블레이드가 달린 디스크 형의 임펠러가 설치된 교반기 내 유동특성을 연구하였으며 블레이드의 개수와 면적이 달라지면서 유동계수 등의 토출 지표가 크게 변하는 경향을 확인하였다. Mununga 등(6)은 배플이 없고 flat paddle이 설치된 교반기 내에서 임펠러의 설치 위치와 교반기 바닥 사이의 거리에 따라 토출유량을 연구하였고, 교반기 내 유동에 대해 레이놀즈수와 임펠러의 크기가 지배적인 변수로 작용한다는 것을 확인하였다. Aubin 등(7)은 임펠러에 의해 토출되는 유동의 방향에 따라 교반성능을 비교하여, 상향 토출유동이 하향 토출보다 낮은 유동계수가 나타나고 많은 동력이 요구되기 때문에 교반 효율 측면에서 하향 유동이 우수하다는 결과를 도출하였다.
터빈 타입의 임펠러는 블레이드의 피칭각의 변화만으로 교반기 내 다양한 유동형태를 형성시킬 수 있어 다양한 교반 상황을 만족시킬 수 있다. 터빈 임펠러 중에서 flat turbine을 기본형상으로 설정하여 블레이드의 피칭각도 변화와 임펠러의 종류에 따른 유동장 특성을 도출하고 교반성능 및 효율을 비교 분석하였다. 교반성능과 효율을 분석하기 위하여 유동계수(Flow Coefficient), 순환계수(Circulation Coefficient)와 동력계수(Power Coefficient)의 무차원계수를 도입하였다. 또한 세 가지 무차원계수를 통해 교반의 효율적 측면이 고려된 토출유용도(Pumping Effectiveness)와 순환유용도(Circulation Effectiveness)을 유도하고 교반기의 형상에 따라 비교하여 효율이 우수한 임펠러의 형상을 규명하였다.
2. 수치해석
2.1 해석 모델 및 경계조건
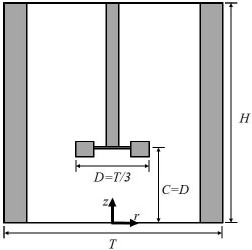
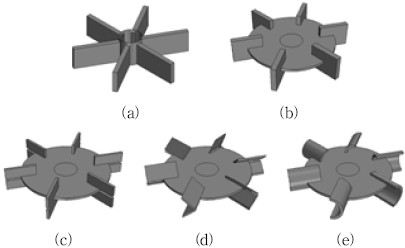
Fig. 1은 본 연구에서 사용된 교반기 형상의 개략도이다. 전체적인 교반기의 내부 구조는 교반기의 높이와 동일한 네 개의 배플과 중심축 끝에 여섯 개의 블레이드가 달린 임펠러가 설치되어 있는 형상이다. 본 연구에서 사용된 임펠러의 형상은 Fig. 2에 나타나있다. Fig. 2(a)는 flat paddle로써 보 형태로 큰 체적 유량이 필요한 공정에서 많이 사용된다. Fig. 2(b), (c), (d), (e)는 터빈형으로 상대적으로 flat paddle에 비해 임펠러에서 토출되는 유량은 작지면 큰 전단력이 필요한 공정에서 사용된다. 터빈형은 블레이드의 형상에 따라 명칭이 다르다. Fig. 2(b)는 가장 기본적인 터빈형으로 둥근 원판의 끝에 블레이드가 달린 형상으로 본 연구에서 임펠러의 기본 형상으로 설정되었다. Fig. 2(c)는 dual flat turbine으로 flat turbine에서 블레이드가 상ㆍ하로 나뉜 형상이다. Fig. 2(d)는 dual pitched turbine이며 dual flat turbine에서 블레이드가 45°로 회전된 형상이다. Fig. 2(e)는 concave turbine으로써 블레이드가 반원통인 형상이다. 기본 형상인 flat turbine의 크기와 치수는 Table 1에 나타나있다. 또한 다른 종류의 임펠러의 크기는 임펠러의 지름(D)과 블레이드의 원주방향의 전투영 면적에 대해 flat turbine과 동일하게 설정하였다. 본 연구에서 교반 성능 및 교반 효율이 우수한 임펠러 형상을 도출하기 위하여 Fig. 2(b)의 flat turbine에 대하여 블레이드 피칭각도를 0˚, 15˚, 30˚, 45˚, 55˚, 60˚, 65˚, 70˚, 75˚로 변화시켰다. 뿐만 아니라 Fig. 2와 같이 flat paddle, dual flat turbine, dual pitched turbine, concave turbine 등의 다양한 임펠러 종류에 따른 교반 성능 및 효율도 비교하였다. 교반기 내 유체는 등온 상태의 물을 가정하였다. 임펠러의 교반성능만을 연구하기 위하여 유체가 가득 차있는 용기를 가정하여 교반기는 전체적으로 벽 조건으로 설정되었다.
Schematic of a stirred vessel
Various types of impellers. (a) flat paddle; (b) flat turbine; (c) dual flat turbine; (d) dual pitched turbine; (e) concave turbine
2.2 지배 방정식 및 수치해석 기법
교반 현상을 예측하기 위해 교반기는 삼차원으로 모델링되었으며, 비압축성을 가정한 연속 방정식과 Navier-Stokes 방정식을 계산하였다. 본 연구에서 교반기 내부유동의 레이놀즈수는 18,000이상이므로, 난류 효과를 고려하기 위하여 Standard k-ε 난류 모델을 적용하였다. 임펠러의 회전 효과는 주로 터보기계, 교반기, 펌프와 덕트 팬 등에 많이 적용되는 MRF을 사용하였다. 이 방법을 교반기 내부를 회전 영역과 비회전 영역으로 두 개의 영역으로 나누고 회전 영역에 MRF 회전 조건을 설정함으로써 회전 영역의 모멘트 방정식에 Coriolis 힘과 원심력을 추가하여 계산한다. 임펠러의 회전은 축 함께 18.8 rad/s의 각속도로 회전하여 교반기 내부 유동장을 형성한다. 위에서 언급한 방정식을 계산하기 위하여, 상용 CFD 프로그램인 STAR-CCM+ 6.04 버전을 사용하였다. 임펠러의 복잡한 형상을 계산하기 위하여 다면체 격자가 사용하였고, 교반기의 전체 격자는 약 150 만개로 구성하였다.
Dimensions of a stirred vessel
Flow coefficient; (a) Schematic description of flow rate by 45° pitched turbine and (b) control surface to estimate the discharge rate
2.3 교반성능 변수의 정의
교반기의 성능은 내부에 형성되는 유동특성에 의해 결정되며, 이에 본 연구에서는 임펠러 형상에 따른 교반성능을 평가하기 위하여, 임펠러에 의해 발생하는 토출유동과 교반기 내부에 순환유동, 임펠러의 소비 동력 및 교반효율을 나타내는 변수를 다음과 같이 정의하였다(5)(8).
교반기 내 유동장은 임펠러의 형상과 작동조건이 지배적인 변수로 작용한다. 특히 물질의 교반이 주로 임펠러의 회전에 의해서 좌우되기 때문에, 교반성능을 분석하기 위해서는 작동 유체를 토출하는 임펠러의 능력이 먼저 정의되어야 한다. 임펠러의 토출 능력을 나타내는 지표로 무차원된 유동계수(Flow Coefficient)를 사용하며 이는 임펠러 회전 속도와 임펠러의 지름에 대한 토출유량으로 나타난다. 유동계수는 다음과 같이 표현된다.
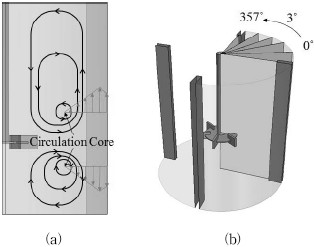
Circulation coefficient; (a) Schematics of circulation in a stirred vessel and (b) monitoring plains for averaged flow field in circumferential direction
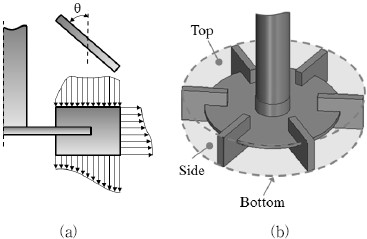
여기서 Qp는 각 표면에서 나타나는 토출유량의 합으로 임펠러에 의한 총 토출유량이고, N과 D는 각각 임펠러의 회전 각속도와 임펠러의 지름이다. 토출 유량은 임펠러 내부로 유입되는 유량을 제외하고 토출되는 유량만을 계산해 토출유량의 합을 계산하였다. 임펠러 주위의 유동형태는 블레이드의 피칭각도와 임펠러 종류에 따라 유체가 토출되는 방향이 다르며, 작지만 상향 토출되는 유동도 존재한다. 45°피치된 터빈의 경우, 토출유동의 속도 프로파일이 Fig. 3(a)에 나타난 것처럼 주로 반경 방향과 하향 방향으로 나타난다. 본 연구에서는 임펠러 상부와 하부 측면부에 Fig. 3(b)에 나타낸 것과 같이 임펠러 주변에 검사 표면을 설정하여, 모든 방향에 대한 토출유량을 계산하였다.
Fig. 4(a)는 flat turbine에 의하여 형성되는 유동장을 나타내는 그림이다. 교반기의 전체적인 유동형태는 교반기 내 유동의 순환 구조에 따라 나타나게 된다. 본 논문에서 임펠러의 기본형상으로 설정한 flat turbine의 경우 Fig. 4(a)와 같이 임펠러를 기준으로 상단과 하단에 순환유동이 발생한다. 순환유동은 임펠러에 의해 토출된 유동이 교반기의 벽에 부딪쳐 각각 교반기의 상단과 하단으로 이동하여 교반기 중심으로 돌아오는 구조이다. 따라서 순환유동은 임펠러에 의해 토출되는 유동의 방향 및 속도뿐만 아니라 임펠러와 교반기의 크기 비율과 교반기의 벽 형상 등의 형상적 요인에 영향을 받는다. 순환에 의한 유량은 Fig. 4(a)에서 도식된 속도 프로파일과 같이 순환유동의 중심점에서 교반기 벽까지의 거리와 순환 방향 속도의 조합으로 계산된다. 이러한 교반기 내 유동 순환을 순환계수(Circulation Coefficient)로 나타낼 수 있으며, 다음과 같이 표현된다.
Averaged flow patterns by different pitching angles(ɵ) of blade
여기서 Qc는 교반기 상단과 하단으로 순환하는 유량의 총합이다. 교반기 내의 유동장은 임펠러와 교반기 벽, 배플의 상호 작용에 의해 복잡한 유동장이 형성되어 모든 위치에서 유동장이 동일하지 않다. 따라서 교반기 내 대표할 수 있는 순환유동을 구하기 위해서는 대표 유동장이 필요하다. 이 대표 유동장을 도출하기 위해 Fig. 4(b)와 같이 원주 방향으로 3°간격으로 120개의 평면을 생성하여 각각의 유동장을 계산하였다. 계산된 120개 유동장을 원주방향으로 평균하여 대표 유동장을 도출할 수 있으며, 이 대표 유동장을 바탕으로 순환계수를 구하였다.
임펠러는 회전하면서 작동 유체의 저항을 받게 되는데, 이 저항은 임펠러의 압력과 전단응력으로 나타난다. 또한 이 저항은 임펠러의 형상과 작동 유체의 점성 등의 물성치에 따라 다르며, 이와 함께 임펠러를 회전시키기 위한 소비 동력도 크게 달라진다. 이 소비 동력을 나타내는 지표로 무차원된 동력계수(Power Coefficient)는 다음과 같이 표현된다.
여기서 P=2πNW는 소비 동력이고, ρ는 유체의 밀도, D는 임펠러의 지름, W는 임펠러에 작용하는 토크이다.
단순히 임펠러의 토출 능력을 증가시키는 것이 목적이라면 임펠러를 더 크게 설계하고 빠르게 회전시키면 된다. 하지만 임펠러의 커진 형상에 비례하여 작동 유체에 의한 저항력도 증가하므로, 임펠러의 작동 효율은 나빠질 수 있다. 따라서 소비 동력은 작지면 임펠러의 토출 능력이 높은 형상에 대한 설계가 필요하며, 이를 위해서 요구 동력 대비 임펠러의 토출 능력을 비교할 수 있는 지표가 필요하다. 토출유용도(Pumping Effectiveness)는 유동계수와 동력계수의 비율로서, 임펠러의 토출 효율을 나타내는 지표로 사용되고 다음과 같이 표현된다.
토출유용도 외에도 유동을 순환시키는 효율을 나타내는 순환유용도(Circulation Effectiveness)가 있다. 순환유동은 임펠러에 의해 토출된 유동이 교반기 벽에 부딪쳐 순환하는 구조이므로 토출유동과 교반기 벽 사이의 형상적 특징이 고려되어야 한다. 이러한 형상적 특징은 내부유동에 주요한 영향을 줄 수 있는 임펠러의 길이와 교반 용기의 지름의 비율로서 나타난다. 순환유용도는 요구 동력에 대한 순환계수를 나타낸 무차원계수로, 토출유용도와 유사하게 나타나며 다음과 같이 표현된다.
여기서 D와 T는 각각 임펠러와 교반 용기의 지름이다.
토출유용도와 순환유용도는 임펠러의 의해 발생된 유동이 교반기를 순환하여 교반되는 과정을 의미하며, 이는 형상적 요인에 의한 교반성능을 비교하기 위해 사용된다.
3. 결과 및 토의
3.1 블레이드 피칭각도에 따른 교반성능 비교
블레이드 피칭각도에 따른 결과를 분석하기 위해서 블레이드의 피칭각도 변화에 따라 형성되는 유동장과 임펠러에 의한 토출유동의 속도 프로파일을 살펴보고, 무차원계수를 통해 교반성능을 비교하였다.
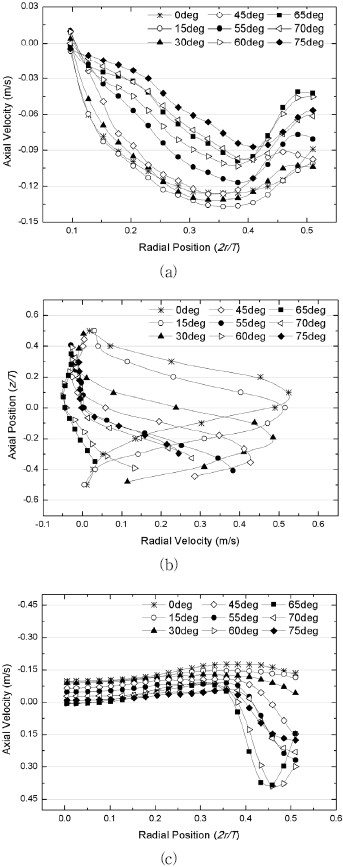
Velocity profile by flat turbine with different pitching angles of blade at (a) the top surface; (b) the side surface; (c) the bottom surface
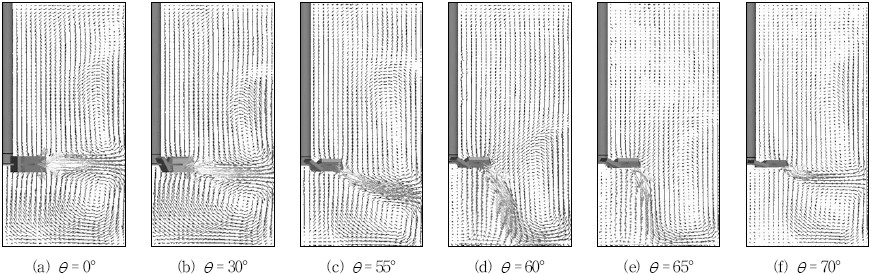
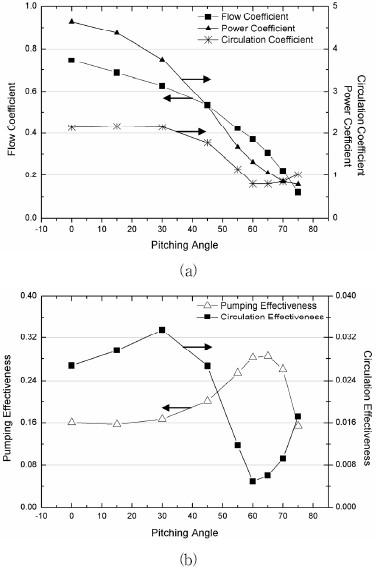
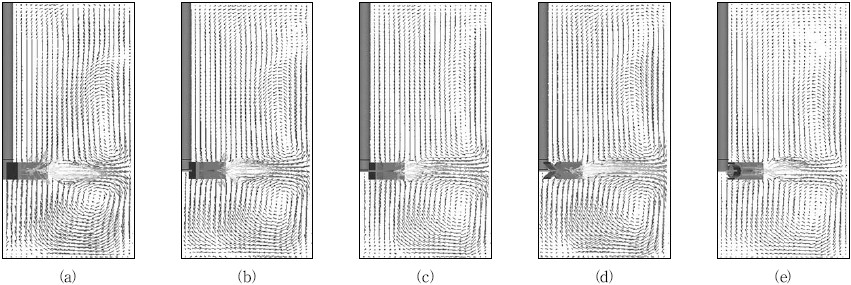
교반기 내부 유동장은 주로 임펠러의 회전에 의해 형성되며 유동장의 형태는 임펠러의 형상에 따라 다양한 다양하다. 본 연구에서는 사용된 임펠러는 블레이드가 수직하거나 피칭된 형태이기 때문에 주로 축 방향 유동과 반경 방향 유동을 발생시킨다. Fig. 5는 flat turbine에서 블레이드의 피칭각도 변화에 대하여 교반기 내부의 대표 유동장을 나타낸 그림이다. 블레이드가 수직으로 설치된 flat turbine은 Fig. 5(a)와 같이 임펠러와 수평한 위치에서 교반기 벽으로 토출유량을 발생시킨다. 토출된 유동은 교반기 벽에 부딪쳐 교반기의 상단과 하단으로 나뉘어져 이동하다가 회전축이 있는 교반기 중심으로 되돌아오는 순환유동을 형성한다. Fig. 5(a)∼(f)는 블레이드 각도가 순서대로 0°, 30°, 55°, 60° 65°, 70°로 피치된 경우의 유동형태를 나타낸 그림이다. 전체적인 유동은 임펠러와 수평하게 토출되는 반경 방향 유동이 블레이드의 피칭각도가 증가하면서 축 방향 유동으로 변하는 경향을 보인다. 특히 55°에서 60°로 피칭각도가 증가하는 시점에서 토출유동은 반경 방향에서 축 방향으로 바뀐다. 또한 교반기의 상ㆍ하단에 발생하는 두 개의 순환유동이 토출방향이 변하면서 교반기 바닥에 부딪쳐 하단에 한 개의 순환유동을 발생한다. 반면 65°에서 70°로 피칭각도가 증가하는 시점에서는 토출유동이 축 방향에서 반경 방향으로 바뀌며 55°에서 60°로 피칭각도가 변하는 경우와는 상반되는 유동장을 형성한다.
(a) Variations of flow, circulation and power coefficient; (b) pumping effectiveness and circulation effectiveness by flat turbine with different pitching angles of blade
임펠러 회전에 의한 유동 발생 형태를 구체적으로 확인하기 위하여 Fig. 6와 같이 임펠러 주변의 검사 표면에서 추출된 각 방향의 속도 프로파일을 나타내었다. Fig. 6(a)는 윗면 검사표면에서 나타난 속도 프로파일로서 전체적으로 임펠러로 유입되는 유동형태를 나타낸다. 각도에 따라 살펴보면, 45°이전의 피칭각도가 설정된 그래프에서 비교적 높은 유입 속도를 나타내는데 반면 45°이후에 유입속도가 낮아지는 경향이 나타난다. Fig. 6(b)는 측면 검사표면에서 나타난 속도 프로파일로서 전체적으로 토출되는 유동형태를 나타내지만 블레이드의 피칭각도 변화에 따라 속도 프로파일이 매우 다르게 형성된다. 0°의 경우 임펠러의 중심에서 최대 토출 속도를 나타내면서 속도 프로파일이 좌우 대칭을 이룬다. 피칭 각도가 증가함에 따라 최대 토출 속도의 위치가 낮아지는데, 55°의 피칭각도의 경우 블레이드 바닥면에서 최대 토출 속도가 나타난다. 또한 피칭각도의 증가에 따라 토출되는 임펠러의 높이가 낮아지고 최대 토출 속도가 작아진다. 이는 Fig. 5에서 나타난 속도장과 같이 피칭각도의 증가에 비례하여 유체를 토출 할 수 있는 임펠러의 길이가 작아지며, 반경 방향의 유동이 축 방향의 유동으로 변하기 때문이다. Fig. 6(c)는 아랫면 검사표면에서 나타난 속도 프로파일로서, 임펠러의 회전축을 기준으로 블레이드의 약 2/3지점까지 임펠러로 유체가 유입되는 속도가 나타난 이후 토출유동이 나타난다. 특히 토출유동은 블레이드의 피칭각도에 따라 증가하다가 65°의 피칭각도에서 최대를 보이고 다시 감소한다. 이는 Fig. 5에서 토출유동의 방향이 반경 방향에서 축 방향으로 바뀐 후 65°에서 다시 반경 방향으로 바뀌는 경향과 일치한다.
Averaged flow patterns by different impeller types: (a) flat paddle; (b) flat turbine; (c) dual flat turbine; (d) dual pitched turbine; (e) concave turbine
블레이드의 피칭각도에 따라 유동장의 경향성과 임펠러에 의한 토출유동의 속도 프로파일을 연결하여 유동장을 비교 분석하였다. 교반기 내부의 교반성능을 수치적으로 비교하기 위해서 2.2절에서 서술한 것과 같이 유동계수, 순환계수와 동력계수로 나타내고, 이들의 조합으로 효율적 측면을 고려한 토출유용도와 순환유용도를 도출하여 Fig. 7과 같이 나타내었다. Fig. 7(a)는 블레이드의 피칭각도에 따라 세 가지 무차원계수를 나타낸 그래프이며, 전체적으로 피칭각도의 증가에 따라 무차원계수들이 감소하는 경향을 나타내지만 감소형태는 각각 다르다. 먼저, 유동계수가 45°를 기점으로 39%의 완만한 감소 이후에 77%의 급감하는 이유는 0°∼45°사이에 평균한 속도가 윗면의 검사표면에서 14%, 측면에서 37%, 아랫면에서 88%가 감소하는데 반해 55°∼75°사이의 평균된 속도가 윗면의 검사표면에서 32%, 측면에서 77%, 아랫면에서 125%의 비교적 큰 감소를 보이기 때문이다. 순환계수는 토출되는 유동이 교반기 벽에 부딪쳐 순환하는 능력을 나타내므로, 피칭각도 증가에 따라 전체적으로 감소하다가 60°의 피칭각도에서 급감한다. 이는 교반기의 측벽으로 토출되는 유동이 교반기의 바닥으로 향하는 유동으로 바뀌고, 이로 인해 상ㆍ하단에 발생하던 두 개의 순환유동이 교반기 하단에 하나의 순환유동으로 변하기 때문이다. 동력계수는 형상적인 요인에 의해 30°∼60°사이에서 급감하는 경향이 나타난다. 블레이드의 전투영 면적이 0°∼30°사이에서 5%, 30°∼60°사이에서 21%, 60°∼75°사이에서 6%가 감소하여, 동력계수는 순서대로 23%, 64%, 39%로 감소하였다. 이를 통해 전투영 면적의 감소는 동력계수의 감소로 이어지는 경향을 도출할 수 있다. 앞에서 언급한 세 가지의 무차원계수들은 피칭각도의 증가에 따라 감소하는 경향만이 나타났다. 하지만 Fig. 7(b)는 임펠러의 효율이 고려된 무차원계수의 그래프로서 특정 피칭각도에서 우수한 교반 효율이 나타난다. 임펠러를 사용하는 산업에서는 소비 동력을 고려한 효율적인 측면이 중요한다. 이러한 측면에서 임펠러의 토출 효율은 토출유용도로 나타낼 수 있으며, 3.2항에서 정의한 것과 같이 유동계수과 동력계수의 비율로서 나타난다. Fig. 7(b)에서 65° 피칭각도의 임펠러가 가장 큰 토출유용도를 나타내는데, 유동계수 대비 동력계수가 비교적 작기 때문이다. 이를 통해 65° 피치된 임펠러가 동력 절약형 임펠러임을 알 수 있다. 또한 순환 유동의 효율적 측면은 순환유용도로 나타낼 수 있으며 30°피칭각도의 임펠러가 가장 큰 순환유용도를 나타난다. 이는 비교적 큰 동력계수 대비 높은 순환계수로 나타나므로 성능 효율형 임펠러임을 알 수 있다.
Velocity profile by different types of impeller at (a) the top surface; (b) the side surface; (c) the bottom surface
3.2 임펠러 종류에 따른 교반성능 비교
임펠러의 종류에 따른 교반성능 및 효율을 비교 분석하기 위하여 유동장과 토출 속도의 프로파일을 살펴보고, 무차원계수를 통해 교반 성능을 비교하였다.
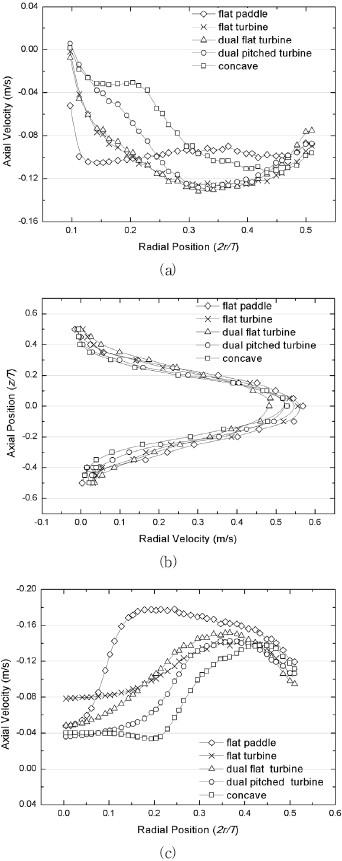
본 연구에서 임펠러의 기본형상으로 설정한 flat turbine과 크기가 동일하지만 다른 종류의 임펠러에 대하여 교반기 내 유동장을 Fig. 8에서 나타내었다. 종류 별로 선정된 임펠러 들은 반경 방향 유동을 발생시키는 형상으로서 Fig. 8에서 나타난 것과 같이 유동장이 전체적으로 유사하며, 임펠러와 동일한 위치에서 토출유동이 발생하고 교반기의 상ㆍ하단에 각각 하나의 순환유동이 나타난다. 하지만 Fig. 8(a)와 같이 보 형태의 임펠러가 유동을 크게 발생시키고, 반대로 Fig. 8(e)와 같이 변형된 형태의 임펠러가 유동을 작게 발생시키는 경향을 나타낸다. 이 경향은 동일한 각속도로 임펠러가 회전할 경우 회전 방향에 대한 임펠러의 면적이 클수록 교반기 내부 유동도 크게 발달한다는 특징을 도출할 수 있다.
(a) Variations of flow, circulation, power coefficient; (b) pumping effectiveness and circulation effectiveness by different types of impeller
임펠러의 종류가 달라지더라도 Fig. 8과 같이 전체적인 유동장은 축 방향 토출유동이 발생되고 두 개의 순환유동이 나타나는 형태가 유사하다. 하지만 토출되는 유동의 속도 프로파일을 보면 Fig. 9과 같이 임펠러 형상에 따른 차이가 나타난다. Fig. 9(a)는 윗면 검사표면에서 나타난 속도 프로파일로서 전체적으로 임펠러로 유입되는 유동형태가 나타낸다. Flat paddle의 경우 속도 프로파일이 임펠러의 전체 길이에 걸쳐 비교적 높은 유입속도로 나타난다. 블레이드의 형상이 유사한 flat turbine과 dual flat turbine의 경우 flat paddle에 비하여 블레이드의 반경 길이가 1/2이기 때문에 중심축에서 임펠러 길이의 2/3부분에서 유입속도가 발달한다. Dual pitched turbine과 concave turbine는 Fig. 2에서 나타낸 임펠러 형상과 같이 flat paddle이 비하여 블레이드 반경 길이가 1/2이며 블레이드가 수직으로 설치된 임펠러와는 달리 둥글게 변형된 형태이다. 이 변형된 형태가 상단으로 유입되는 유동에 대해 방해물로서 작용하여 유입속도를 작게 한다. 이러한 특징으로 dual pitched turbine과 concave turbine의 상단 유입유동은 회전축이 가까운 위치에서 유입속도가 작게 나타나다가 임펠러의 1/2위치에서 속도가 증가하는 경향이 나타난다. Fig. 9(b)는 측면 검사표면에서 나타난 속도 프로파일로서, 모든 임펠러가 임펠러의 중심 높이에서 최대 속도로 반경 방향의 토출유동을 형성한다. Fig. 9(c)는 아랫면 검사표면에서 나타난 속도 프로파일로서 윗면에서 나타난 경향과 유사하게 전체적으로 임펠러로 유입되는 유동형태를 나타낸다. Fig. 9의 각 검사 표면에서 나타나는 유동속도의 프로파일을 종합해보면 flat paddle의 경우 임펠러가 보 형태로서 전체 길이에 대하여 검사 표면의 윗면과 아랫면에서 높은 유입속도와 함께 측면에서는 가장 높은 토출 속도를 나타낸다. 반면 dual flat turbine와 concave turbine의 경우 Fig. 9에서 나타낸 임펠러 형상과 같이 블레이드의 변형된 형상이 유동 방해물로서 작용하기 때문에 윗면과 아랫면에서 유입유동이 작게 나타난다.
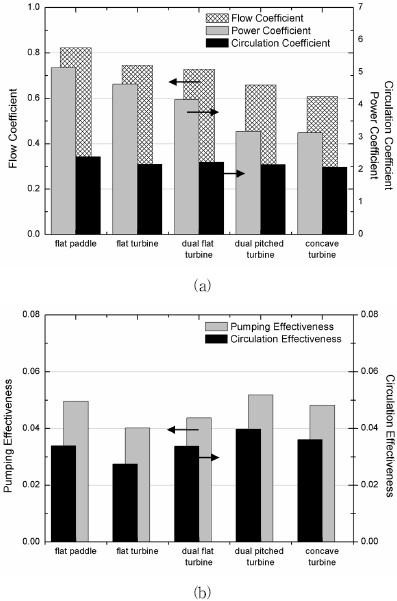
임펠러의 종류에 따른 교반성능을 비교하기 위해 Fig. 10(a)와 같이 유동계수, 순환계수와 동력계수를 나타냈으며, 이들의 조합으로 효율적 측면을 고려한 토출유용도와 순환유용도를 Fig. 10(b)에 나타냈다. Fig. 10(a)를 보면 flat paddle에서 가장 높은 유동계수와 동력계수가 나타난다. 높은 유동계수는 Fig. 9(b)에서 토출되는 유동이 크게 나타난 것이 원인이다. 또한 동력계수가 큰 이유는 Fig. 9(a), (c)와 같이 임펠러의 상ㆍ하단에서 비교적 큰 유입유동으로 인해 임펠러 회전에 대한 저항이 크게 나타났기 때문이다. 반면 dual flat paddle과 concave turbine에서 낮은 유동계수와 동력계수를 나타난 것은 flat paddle을 분석한 내용과 상반되게, 임펠러 형상에 따라 토출되는 유동과 임펠러로 유입되는 유동이 작기 때문이다. 순환계수는 임펠러의 형상이 달라져도 비슷한 크기를 나타나는데, 이는 토출유동의 형태가 유사하며 토출속도의 차이가 교반기 벽에 부딪쳐 감소되기 때문이다. Fig. 10(a)에서 무차원계수가 flat paddle에서 크고 dual flat paddle와 concave turbine에서 작은 경향이 나타나지만 효율적인 요인을 고려하면 Fig. 10(b)와 같이 상반된 경향이 나타난다. Fig. 10(b)에서 토출유용도와 순환유용도가 블레이드 형상이 변경된 dual flat paddle과 concave turbine에서 크게 나타난다. 이는 유동계수의 감소보다 동력계수의 감소가 더 크게 나타나기 때문이며, 변형된 블레이드 형상이 저항으로 작용할 수 있는 유입유동을 작게 만들기 때문이다. 기본 형상인 flat turbine는 flat paddle보다 짧고 수직한 블레이드 형상을 가지고 있기 때문에 유동계수가 크지 않으며, dual flat paddle과 concave turbine에 비하여 블레이드의 상ㆍ하단에서 유입유동의 속도가 크기 때문에 동력계수는 크게 나타난다. 이로 인해 flat turbine은 다른 종류의 임펠러에 비해 교반 효율이 우수하지 않지만 3.1절에서 분석한 내용과 같이 특정 피칭각도에서는 다른 종류에 비하여 우수한 교반 효율을 나타낼 수 있다.
4. 결 론
본 논문에서는 교반기 내 교반 성능을 예측하기 위하여 flat turbine을 임펠러의 기본형상으로 설정하고, 블레이드의 피칭각도의 변화와 임펠러의 종류에 대하여 유동장과 토출유동의 속도 프로파일을 비교 분석하였다. 또한 교반성능 및 효율을 나타내는 무차원계수를 도출하여 경향성을 분석하고, 성능과 효율이 우수한 임펠러 형상을 규명하였다.
Flat turbine의 블레이드 피칭각도에 따른 결과를 통해 피칭각도가 65°에서 최대 토출유용도가 나타나며, 30°에서 최대 순환유용도가 나타난다. 이는 65°피칭각도가 동력 절약형이고 30°피칭각도가 성능 효율형임을 알 수 있다.
반면 임펠러의 종류에 따른 결과는 dual pitched turbine에서 토출유용도와 순환유용도가 가장 우수하게 나타났다. 이를 통해 교반 효율을 향상시키기 위해서는 유입유동을 감소시킬 수 있는 형상의 변화가 필요하다는 결론이 도출된다.
이러한 임펠러의 형상에 따른 교반 성능 및 효율의 결과는 교반기 설계에 대한 기초자료로 활용 될 것으로 사료된다.
Acknowledgments
이 논문은 2009년도 교육과학기술부의 재원으로 한국연구재단의 지원을 받아 ‘다중현상 CFD 연구센터(ERC)’ 과제(No.20090083510)의 일환으로 ㈜하도의 지원을 받아 수행된 연구임.
References
- 김치겸, 원찬식, 허남건, “배플 형상에 따른 교반기 내부 고체입자 분포의 비정상상태 해석”, 한국전산유체공 학회 추계학술대회, (2008), p171-175.
- 장재원, 허남건, 2000, “45° Pitched Paddle 형 교반기 내부유동 해석”, 한국전산유체공학회 추계학술대회, (2000), p109-114.
-
Kumaresan, T., Joshi, J. B., “Effect of Impeller Design on the Flow Pattern and Mixing in Stirred Tanks”, Chemical Engineering, (2006), 115, p173-193.
[https://doi.org/10.1016/j.cej.2005.10.002]
-
Nienow, A. W., “On Impeller Circulation and Mixing Effectiveness in the Turbulent Flow Regime”, Chemical Engineering Science, (1997), 52(15), p2557-2565.
[https://doi.org/10.1016/S0009-2509(97)00072-9]
- Garcia, C. D., Ferrer, E., Barbera, E., “Hydrodynamic Characterization of the Flow induced by a Four-Bladed Disk-Style Turbine”, Chemical Engineering Research and Design, (2001), 79, p269-273.
- Mununga, L., Hourigan, K., Thompson, M., Johnson, S., “Numerical Investigations of Discharge Flow and Circulation Flow in an Unbaffled Mixing Vessel agitated by a Plain Disk”, 2nd International Conference on Heat Transfer Fluid Mechanics and Thermodynamics, paper no. M L1, (2003.).
-
Aubin, J., Mavros, P., Fletcher, D. F., Bertrand, J., Huereb, C., “Effect of Axial Agitator Configuration (Up-Pumping, Down-Pumping, Reverse Rotation) on Flow Patterns generated in Stirred Vessels”, Chemical Engineering Research and Design, (2001), 79(8), p845-856.
[https://doi.org/10.1205/02638760152721046]
- Zadghaffari, R., Moghaddas, J. S., Revstedt, J., “A Study on Liquid-Liquid Mixing in a Stirred Tank with a 6-Blade Rushton Turbine”, Iranian Journal of Chemical Engineering, (2008), 5(4), p827-843.