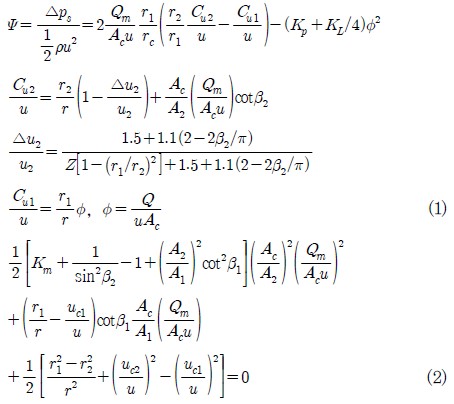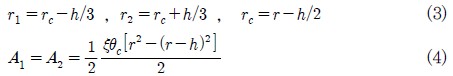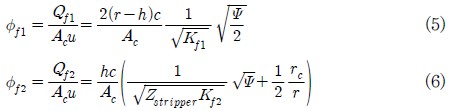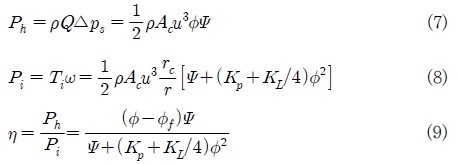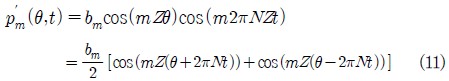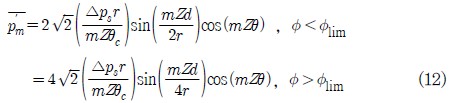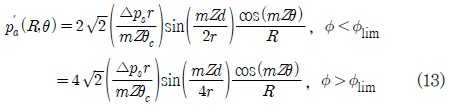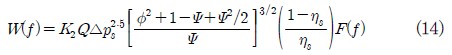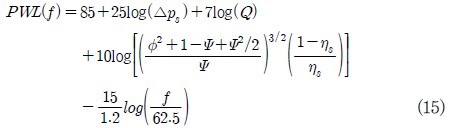Aero-acoustic Performance Analysis Method of Regenerative Blower

1. 서 론

재생형 송풍기는 적은 유량에서도 높은 압력을 생산해 낼 수 있는 성능 특성과 단순한 구조, 쉬운 제작 및 운전으로 인해 화학공장, 환경시설 및 연료전지용 송풍기 등으로 널리 사용되고 있다.

재생형 송풍기는 회전하는 원판에 설치된 다수의 임펠러(impeller)와 임펠러를 감싸고 있는 고정된 채널(fixed channel)사이를 통과하는 유체의 운동량 교환(momentum exchange)에 의해 압력이 상승하는 원리에 의해 작동되며, 이로 인해 유체기계 내부에서 발생하는 강한 난류에 의한 압력손실 및 임펠러/채널 간극을 통한 누설유동이 발생한다. 그리고 이러한 압력손실 및 누설유동의 발생은 재생형 유체기계의 성능저하 및 낮은 효율의 주요한 원인으로 작용하고 있다.

재생형 송풍기의 현장 적용 시 또 다른 단점은 상대적으로 높은 소음도로서, 소음의 발생은 높은 압력의 작동 조건과 기계 내부의 강한 난류에 의해 주로 야기되고, 이러한 소음은 특정한 주파수에 집중되는 이산 주파수 소음(discrete frequency noise)과 넓은 주파수 범위에 분포되는 광대역주파수소음(broadband -noise) 형태로 방사된다.

재생형 송풍기의 성능/효율 향상을 위해서 실험적 방법, 1차원 성능해석 방법 및 3차원 전산유체역학 해석 방법을 이용한 많은 연구들(1-5)이 국내, 외적으로 이루어 졌으나, 대부분의 연구들이 특정한 기계에 대한 측정 및 해석결과들을 보여주고 있어서, 송풍기 설계변수들이 성능에 미치는 영향을 체계적이고 일반적으로 규명하는 연구는 부족한 실정이다.

재생형 송풍기의 소음에 대한 연구는, 원심형 및 축류형 송풍기 소음 연구들에 비해, 거의 이루어지지 않은 실정이다. 그러므로 재생형 송풍기 소음의 저감을 위해서는 소음발생 원인을 파악하고 방사되는 소음의 특성과 크기를 예측할 수 있는 신뢰성 있는 이론적 해석방법의 개발이 필요하며, 이를 통해 송풍기 설계와 성능이 소음에 미치는 영향을 규명하는 연구가 이루어진다면 향후 송풍기 소음 저감에 큰 기여를 할 수 있을 것으로 기대된다.

그러므로 본 연구는 재생형 송풍기의 설계변수들을 정의하고, 설계된 송풍기의 성능을 예측할 수 있는 해석방법을 제안하였다. 성능해석은 운동량 교환이론에 근거한 1차원 해석방법과 압력손실, 누설유동에 대한 모델들을 결합하여 수행하였고, 압력손실 및 누설유동 모델링 시 송풍기 설계변수들의 영향을 고려하였다. 또한 재생형 송풍기의 소음 예측을 위해서는, 예측된 송풍기 성능특성을 토대로, 임펠러 회전수에 비례하는 주파수에서 발생하는 이산 주파수 소음 모델과 송풍기 내부 난류에 의한 광대역주파수 소음 모델을 제안하였다. 본 연구에 의해 제안된 성능 및 소음해석 방법은 송풍기 설계과정과 결합되어 FANDAS code 의 GUI 형태로 구현되었고, 본 방법에 의해 예측된 성능 및 소음해석결과들은 실제 송풍기의 시험결과들과 매우 잘 일치하였다.

2. 설계, 성능 및 소음해석 방법

2.1 설계변수 및 방법

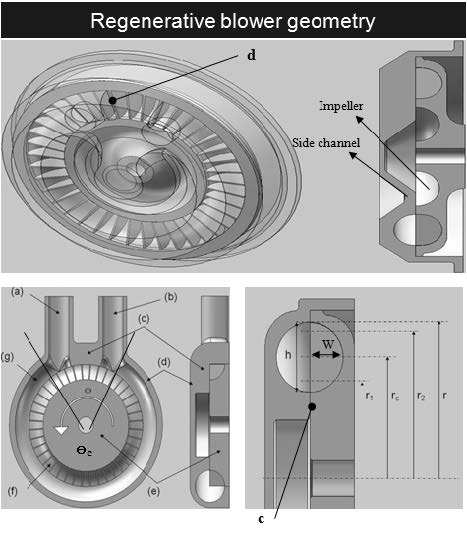
본 연구에서 다루는 재생형 송풍기는 사이드채널(side channel)형태로서(Fig.1 참조), 회전축에 반경 r 인 원판이 설치되고 원판의 접선방향을 따라 Z개의 임펠러가 두께 d 로 가공된다. Fig. 1 에서 보여 지는 것처럼, 임펠러의 단면을 반 타원(half of ellipse)으로 설계하는 경우에는 임펠러 단면의 길이(h)와 폭 (W)이 설계변수로 고려될 수 있다. 일반적으로 임펠러는 원판의 접선방향 기준으로 입, 출구각도가 90deg를 가지도록 설계되나, 송풍기 성능 향상을 위해서는 임펠러의 입구 각도(β₁)와 출구 각도(β₂)를 90deg 와 다르게 설계할 수도 있다.(6)

임펠러 주위에 설치되는 사이드 채널은 일반적으로 임펠러와 동일한 단면을 가지도록 설계되고, 임펠러와 축 방향으로 간극(c)을 유지하도록 설치된다. 또한 송풍기의 입구 및 출구는 사이드 채널 케이싱에 임펠러와 사이드 채널이 이루는 단면적과 동일하게 설치되며, 입구와 출구사이의 스트리퍼(stripper)가 회전축 중심과 이루는 각도(θ_c:extension angle)도 주요한 설계변수로 고려될 수 있다.

Fig. 1

Regenerative blower geometry(5)

Fig. 2

GUI of the FANDAS-Regen

앞서 언급한 재생형 송풍기의 설계변수들을 정리하면 다음과 같고,

- Rotation speed( N )

- Tip diameter( D₂ = 2r )

- Channel height( h )

- Channel width( W )

- Impeller blade inlet angle( β₁ )

- Impeller blade outlet angle( β₂ )

- No. of impeller blades( Z )

- Impeller blade thickness( d )

- Axial clearance( c )

- Extension angle( θ_c )

이러한 설계변수들을 FANDAS GUI 의 입력창을 통해 입력한 후 설계된 송풍기의 3차원 형상은 Fig. 2 에 나타나 있다.

2.2 성능해석 방법

설계된 재생형 송풍기의 성능 해석을 위해서는 운동량 교환이론(17)을 사용하였다.

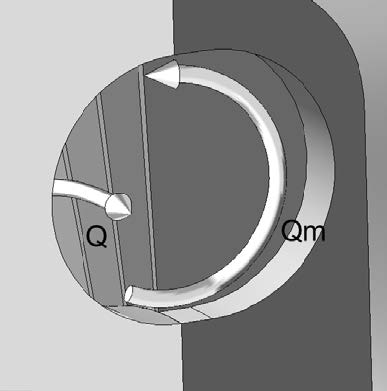
Fig. 3에서 도시된 것처럼, 채널의 단면을 따라 접선방향으로 이동하는 공기 흐름(유량=Q)과 채널과 임펠러의 타원 단면을 따라 순환하는 공기 흐름(유량=Q_m)간의 운동량 교환에 의해 공기의 압력이 순차적으로 증가하며, Z개의 임펠러를 거친 후 송풍기 출구를 통해 토출되는 공기의 정압은 식(1), (2)에 의해 다음과 같이 표현된다.

Fig. 3

Tangential(Q) and circulatory(Qm) flows(1)

이때 Ψ, Φ 는 송풍기의 압력, 유량계수를 나타내며, ρ 는 공기의 밀도를, u 는 임펠러 팁의 회전속도를, A_c 는 사이드 채널의 단면을 의미한다.

또한 식(1), (2) 의 r₁, r₂ 및 A₁, A₂ 는 임펠러 내부를 통과하는 순환류의 입구, 출구에서의 평균반경 및 임펠러 내부에서의 유동면적으로 다음과 같이 정의될 수 있다.

여기서 ξ 는 임펠러 두께를 고려한 유동면적의 축소계수를 의미한다.

송풍기 내부의 누설유동( Q_f )은 임펠러와 사이드채널간의 축 방향 간극을 통한 것( 식5 )과 스트리퍼를 통한 것( 식6 )으로 나누어 생각할 수 있으며,

Table 1

Present loss coefficient models

이때 Z_stripper 는 스트리퍼 영역에서의 임펠러의 개수를 의미한다.

식(1)의 K_p 및 K_L 은 압력손실 및 누설손실 계수로서 이러한 값들은 송풍기 설계변수에 의해 좌우되므로, 본 연구에서는 기존의 실험적 결과들(3458)을 응용하여, l 계수들을 Table 1 같이 송풍기 설계변수들의 상관관계식으로 모델링하였다

앞서 계산된 성능인자들을 바탕으로, 유체, 입력 동력(P_h, P_i) 및 효율(η)은 다음과 같이 구해진다.

2.3 소음해석 방법

본 연구에서는 재생형 송풍기의 소음을 회전수와 임펠러의 개수의 곱에 비례하는 BPF 주파수(BPF; blade passing frequency)에서 발생하는 이산주파수 소음과 넓은 주파수 범위에 분포되는 광대역주파수 소음으로 나누어서 고려하였다.

2.3.1 이산주파수 소음

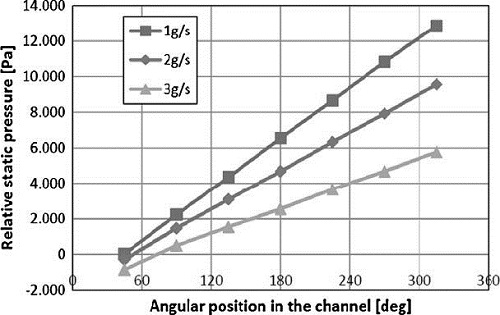
이산주파수 소음은 임펠러와 임펠러사이에 형성되는 압력차가 회전하며 발생되는 소음으로서, 일반적으로 재생형 송풍기의 접선방향을 따른 압력은 선형적으로 상승하므로(Fig. 4 참조), 각 임펠러 마다 동일한 압력상승이 일어남을 알 수 있다.

Fig. 4

Pressure rise along tangential direction(2)

그러므로 임펠러 블레이드 두께(d)를 사이로 전체 송풍기 압력상승(Δp_s)을 유효 임펠러 블레이드의 개수(Z_e)로 나누어 구해지는 압력차가 걸린다고 볼 수 있다. 이때 유효 임펠러 개수는 스트리퍼 영역을 제외한 실제 압력상승을 담당하는 임펠러 블레이드의 개수를 의미하며, Z_e=Zθ_c/2π 로 정의된다.

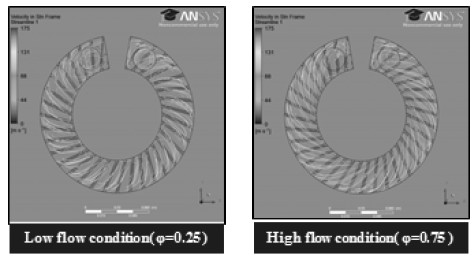
그러나 재생형 송풍기의 경우 적은 유량에서는 공기의 순환유동이 각 임펠러 마다 형성이 되며 압력상승이 이루어지지만(1regeneration/1pitch), 유량이 어느 이상 증가되면 공기의 순환유동이 임펠러 2개마다 한번 씩 형성되며 압력이 상승(1regeneration/ 2pitch)하는 현상이 관찰된다(Fig. 5 참조).

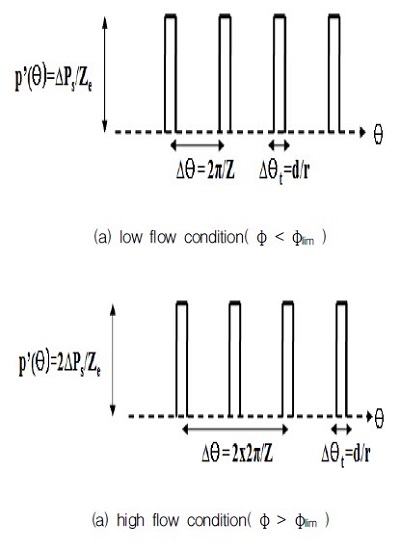
이러한 재생형 송풍기의 유량에 따른 순환유동 현상의 천이과정을 감안하여 인접한 임펠러 블레이드 두께 양단에 걸리는 압력차( 또는 압력 섭동 )를 모델링하면, Fig. 6 과 같은 접선방향에 따른 직사각형 모양의 압력차 형태를 고려할 수 있다.

앞서 2.2절에서 예측된 전체 송풍기 압력상승(Δp_s) 값을 토대로, Fig. 6에서 가정한 직사각형 압력차 형태에 대해 접선방향 각도에 대한 모드해석(9)을 수행하면, 다음과 같은 결과를 얻을 수 있다.

Fig. 5

Regeneration behavior of circulatory flow(2)

Fig. 6

Rectangular type pressure pattern of air between adjacent impeller blades

또한 식(10)에서 얻어진 결과를 이용하여 임펠러의 회전을 고려한 압력 섭동( pressure fluctuation )은 다음과 같이 표현되고,

이때 압력섭동의 시간에 따른 rms( root mean square ) 값은 아래와 같다.

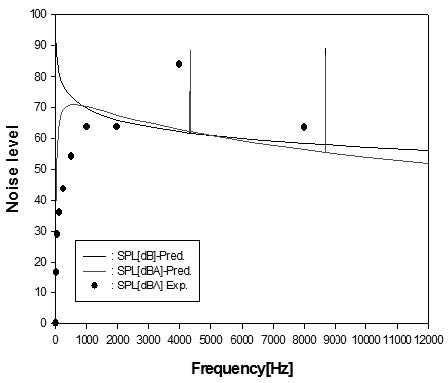
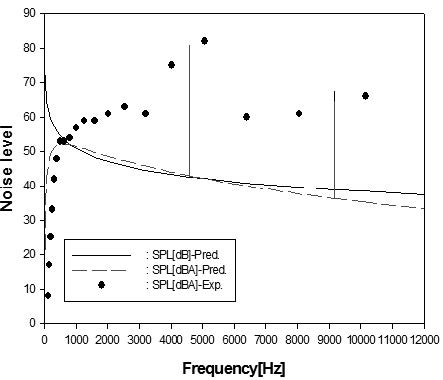
이때 블레이드통과주파수( BPF )는 NZ 으로 정의되며, m=1 인 경우는 BPF 기초모드( fundamental mode )를 의미하며, m=2,3,4.... 는 BPF 배음으로서 조화모드( harmonic modes )를 의미한다. 그리고 임펠러 블레이드간의 압력차 형태가 변화되는 유량계수( φ_lim )는 0.75 로 가정하였다.(2)

식(9)를 통해 얻어진 압력 섭동 값은 소음원에서 얻어진 값 이므로, 송풍기로부터 먼 거리로 방사되는 음압은 식(13)과 같이 구할 수 있고, 더 나아가 음압 레벨( SPL )과 음향 출력 레벨( PWL )도 정의에 의해 쉽게 구할 수 있다.

2.3.2 광대역주파수 소음

광대역주파수 소음은 임펠러와 사이드채널 내부에서 발생하는 난류에 의해 야기되며, 팬 소음의 상사법칙(fan noise similarity rule)에 따르면, 특정한 주파수에서의 음향출력, W(f), 은 다음과 같이 표현될 수 있다.(10)

식(10)의 상수, K²와 주파수 특성, F(f)는 실험적으로 결정되어야 하는 값이나, 재생형 송풍기의 소음관련 기존의 실험적 연구가 전무한 실정이므로, 본 연구에서는 Mugridge(10) 에 의해 제안된 원심형 송풍기의 상관관계식을 토대로 다음과 같은 모델을 제안하였다.

이때 전체 압력상승(Δp_s), 유량(Q), 유량계수(φ), 압력계수(Ψ) 및 정압효율(η_s)은 앞서 2.2절의 성능해석결과로부터 얻어지며, f 는 소음이 발생되는 주파수를 의미한다.

3. 해석결과 및 고찰

본 해석방법을 2가지 실제 황해전기의 재생형 송풍기에 적용하였다. 송풍기는 6673, 7052rpm에서 작동하고, 임펠러의 팁 직경(D₂=2r)은 11.1, 10.4cm 로, 사이드 채널의 높이(h)는 8.0, 7.5 cm 로 설계되었고, 2가지 송풍기 모두 임펠러 개수(Z), 확장각(θ_c), 축 간격(c)은 39, 290deg, 0.2mm 로 설치하였다.

Fig. 7

Aero-acoustic performance map of blower operated at 6673 rpm

Fig. 8

Noise spectrum of blower operated at 6673 rpm and design flow condition

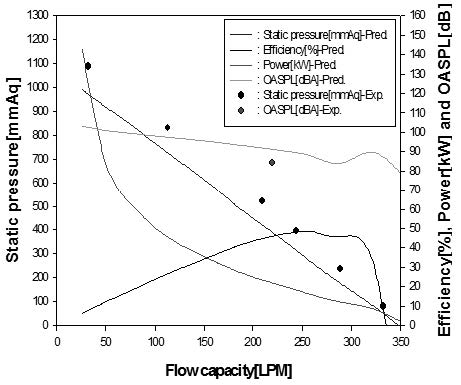
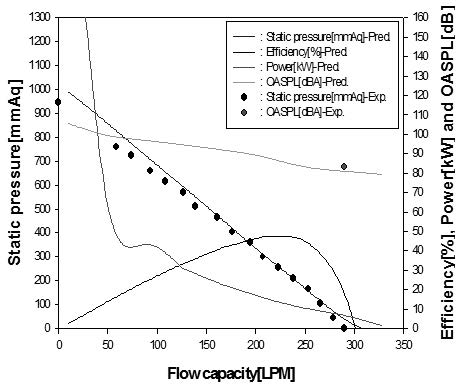
Fig. 7 은 6673rpm 에서 작동하는 송풍기의 유량 변화에 따른 공력음향학적 성능 곡선을 보여주고 있다. 그림에서 보여 지듯이, 정압 예측결과가 측정결과와 전 유량 범위 내에서 잘 일치하고 있으며, 설계점 조건( Q=220LPM, φ=0.61 )에서의 소음예측결과도 측정결과와 잘 일치하고 있다. 참고로 이 경우는 소음 예측이 1 regeneration/ 1 pitch 모드( φ < φ_lim )에서의 소음 모델에 의해 이루어 졌다.

Fig. 8 은 설계점에서의 소음 스펙트럼에 대한 예측과 측정간의 비교를 보여주고 있으며, 본 해석방법이 BPF 에서의 이산주파수 소음의 피크 값을 잘 예측하고 있고, 넓은 주파수 범위에서의 광대역주파수 소음의 특성도 비교적 잘 예측하고 있다.

Fig. 9 는 7052rpm 에서 작동하는 송풍기의 유량 변화에 따른 공력음향학적 성능 곡선을 보여주고 있다. 이 경우에도 해석방법에 의한 정압 예측결과가 측정결과와 잘 일치하고 있으며, 최대 유량점(Q=300LPM,, φ=0.81)에서의 소음 예측결과와 측정결과가 매우 잘 일치하고 있다. 참고로 이 경우는 Fig. 7과 달리 소음 예측이 1regeneration/2pitch 모드(φ > φ_lim)에서의 소음모델에 의해 이루어 졌다.

Fig. 9

Aero-acoustic performance map of blower operated at 7052 rpm

Fig. 10

Noise spectrum of blower operated at 7052 rpm and maximum flow condition

Fig. 10 은 최대 유량점에서의 소음 스펙트럼에 대한 예측과 측정간의 비교를 보여주고 있으며, 본 해석방법이 BPF 에서의 이산주파수 소음의 피크 값을 잘 예측하고 있으나, 높은 주파수 범위에서의 광대역주파수 소음의 특성은 측정에 비해 다소 낮게 예측하고 있으며, 이러한 결과는 최대 유량점에서 출구에서 발생하는 높은 속도의 배출 제트에 의한 광대역주파수 소음의 영향인 것으로 예견된다.

5. 결 론

재생형 송풍기의 설계, 성능 및 소음 예측을 위한 해석방법을 개발하여 GUI 기능이 첨가된 전산화된 시스템(FANDAS-Regen)으로 구성하였다. 성능해석은 운동량 교환이론과 압력손실, 누설손실에 대한 모델들을 결합하여 수행하였다. 소음해석은, 성능해석 결과를 토대로, 본 연구에서 제안한 이산주파수 및 광대역주파수 소음모델들을 이용하여 이루어 졌다. 본 연구의해석 방법들을 실제 재생형 송풍기에 적용하였으며, 예측결과가 성능 및 소음 측정결과와 9 % 및 7 % 오차범위 내에서 잘 일치함을 알 수 있었다. 이러한 결과들로부터, 본 해석방법이 고효율-저소음 재생형 송풍기 개발을 위한 기초 설계 도구로 유용하게 사용될 수 있을 것으로 보여진다.

Acknowledgments

본 연구는 지식경제부 전략산업기술개발 사업의 연구비 지원에 의해 이루어 졌음을 밝힙니다.

References

• Mura, M., Badami, M., “Leakage effects on the performance characteristics of a regenerative blower for the hydrogen recirculation of a PEM fuel cell”, Energy Conversion and Management, (2012), 55, p20-25. [https://doi.org/10.1016/j.enconman.2011.10.002]
• Badami, M., Mura, M., “Comparison between 3D and 1D simulations of a regenerative blower for fuel cell applications”, Energy Conversion and Management, (2012), 55, p93-100. [https://doi.org/10.1016/j.enconman.2011.10.003]
• 심창열, 강신형, “재생 펌프의 유동해석 및 누설유동에 관한 연구”, 대한기계학회논문집 B, (2003), 27(8), p1015-1022.
• 임형수, 강신형, “사이드채널형 재생펌프의 성능특성에 관한 실험적 연구”, 대한기계학회논문집 B, (29), 3, p306-313.
• 최영석, 이경용, 강신형, “사이드채널형 연료펌프의 성능예측”, 유체기계저널, (2003), 6(2), p29-33. [https://doi.org/10.5293/KFMA.2003.6.2.029]
• Badami, M., Mura, M., “Setup and validation of a regenerative compressor model applied to different devices”, Energy Conversion and Management, (2011), 52, p2157-2164. [https://doi.org/10.1016/j.enconman.2010.10.044]
• 이찬, 성형진, 권장혁, 정명균, “재생펌프의 성능해석 및 최적화에 관한 연구”, 대한기계학회논문집, (1991), 15(2), p661-667.
• Idelchik, I.E., Handbook of Hydraulic Resistance, 3rd edition, Begell House, (2001.).
• Wright, S. E., “The acoustic spectrum of axial flow machines”, Journal of Sound and Vibration, (1976), 45(2), p165-223. [https://doi.org/10.1016/0022-460X(76)90596-4]
• Mugridge, B. D., “Noise Characteristics of Axial and Centrifugal Fans as Used in Industry”, Shock and Vibration Digest, (1976), 45(3).