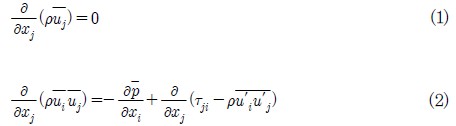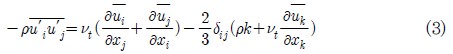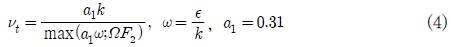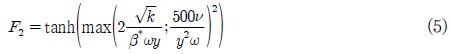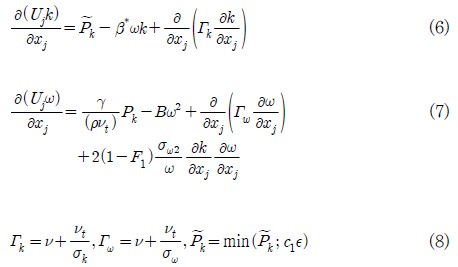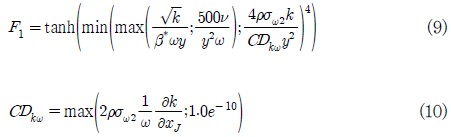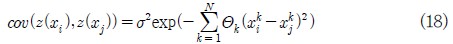Shape Optimization of Inlet Part of a PCHE

1. 서 론

원자력 발전 냉각 시스템은 가스 터빈 사이클을 기반으로 이루어지고 있다. 가스터빈의 경우 기체를 작동유체로 사용하므로 작동 유체의 열용량이 작아 셀 & 튜브 형의 열교환기가 채용될 경우 부피가 커지고 그에 따른 비용이 커진다. HEATRIC(1) 사의 인쇄형 열 교환기 (PCHE: Printed Circuit Heat Exchanger) 는 비슷한 성능의 셀 & 튜브 열 교환기 대비 85% 이상 크기가 작고 가볍게 만들 수 있다는 장점이 있다. 화학적 에칭과 확산 접합 기법으로 제작되는 PCHE는 높은 압력에서도 안정적으로 높은 효율의 성능을 수행할 수 있어 고온 고압에서 운전되는 가스터빈 기반 시스템에 유용하게 쓰일 수 있다.

지난 몇 년간 PCHE의 열 유동 영역에 대한 수치해석 및 실험적 연구가 활발히 이루어져 왔다. 주로 PCHE채널의 형상과 구조에 대한 많은 연구가 진행 되었다. Ishizuka et al.(2)는 CO₂를 냉각 유체로 하여 유량, 압력, 온도에 따른 압력 손실과 열전달 성능을 분석하였다. Nikitin et al.(3)는 초임계 (supercritical) CO₂를 냉각 유체로 하여 실험을 통해 PCHE의 열 유동을 해석하였다. Kim et al.(4)은 에어 포일 형태의 PCHE를 제안하고 기존 지그재그(zigzag) 형태의 유로를 가진 PCHE와 삼차원 수치 해석 방법으로 비교 분석하는 연구를 한 바 있다. 이 연구에서는 에어 포일 형태의 PCHE가 지그재그 채널보다 작은 압력 손실로 동일한 열전달 성능을 보였다. Ngo et al.(5)은 삼차원 RANS (Reynolds–averaged Navier-Stokes)를 이용하여 분석한 결과를 통해 S형의 핀을 가진 PCHE를 제안하고 기존 지그재그 형상 PCHE의 성능과 비교 분석하였다. Pra et al.(6)는 수치 해석을 이용한 여러 사고 예측 시험을 통해 PCHE 의 적절한 작동 환경을 얻어내었다. Kim et al.(7)은 GAMMA code(8)를 사용하여 수치 해석적 방법으로 PCHE의 열 유동 특징을 해석하였다. Lee and Kim(9)은 RANS 해석을 통하여 냉각 채널의 경사각과 타원의 종횡비를 변수로 다중 목적 함수 최적화 기법을 이용하여 지그재그 PCHE 채널의 두 변수에 대한 최적화 연구를 수행하였다. 그 결과 열전달 성능의 향상과 마찰 계수의 감소라는 결과를 얻어내었다.

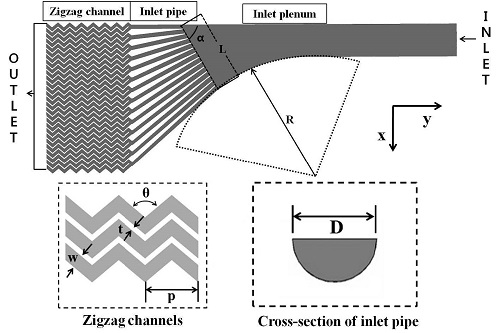
지금까지 진행된 PCHE의 연구는 PCHE의 채널부, 즉, 열 교환이 실제 이루어지는 곳에 대한 연구가 주를 이루었고, PCHE 입구부의 형상이 열전달 성능과 압력손실에 미치는 영향에 대한 연구는 수행된 바 없다. Fig. 1 (10)에 도시한 바와 같이 PCHE의 입구부로 유입된 유동은 각각의 폭이 좁은 채널로 분배되기 때문에 유동 불균일성과 큰 압력강하를 유발할 수 있다. 본 연구에서는 채널로 들어가는 입구부의 형상을 3-D RANS 해석과 대리모델을 이용하여 수치 최적 설계하였으며, 수치모델의 타당성을 증명하기 위하여 PCHE 내의 압력 손실에 대한 Kim et al.(4)의 연구와 비교하여 검증하였다. 최적화를 위한 대리모델로는 크리깅 모델 (KRG)(11)을 사용하였으며 Latin Hypercube Sampling(LHS)(12)을 사용하여 세 개의 설계변수에 대한 실험점들을 생성하였다.

Fig. 1

Example of full size platelet plate(10)

2. 수치해석방법

본 연구에서는 PCHE 입구부 형상이 유동에 미치는 영향을 분석하기 위하여 ANSYS CFX-11.0(13) 상용 CFD 코드가 사용되었으며 정상상태, 비압축성 난류 유동에 대한 지배 방정식(연속 방정식과 운동량 방정식)은 다음과 같다.

여기서, τ_ij 는 층류전단응력이고, 레이놀즈 응력 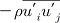항은 식(3)과 같이 나타낼 수 있다.

난류 모델로는 Shear Stress Transport (SST)(14) 모델이 사용되었다. SST 모델은 함수 F₁과 F₂를 사용하여 k-ε 과 k-ω 모델을 결합하여 두 모델의 장점만을 취해 만들어진 모델이다. k-ω 모델은 벽 근처에서 적용되고 k-ε 모델은 벽에서 떨어진 부분에서 적용되도록 모델이 복합적으로 구성되었다. Bardina, et al.(15)은 다른 모델들과 비교하여SST모델이 벽 근처에서의 역압력구배로 인한 유동박리의 예측이 뛰어나다는 것을 보고한 바 있다. 식 (3)의 난류 점성항(ν_t)은 난류운동에너지(k)와 난류소산율 및 난류주기 ω로 아래와 같이 정의 될 수 있다.

F₂ 항은 다음과 같이 벽으로부터의 거리 y로 정의 될 수 있다.

두 개의 수송방정식인 난류운동에너지와 난류소산률 방정식은 다음과 같다.

여기서 P_k 는 난류운동에너지 생성률이고, F₁은 다음과 같이 정의된다.

여기서 모델계수들, σ_k1, σ_ω1, γ₁, β₁, β^*, c₁, σ_k2, σ_ω2, k, γ₂, β₂, β^*에 대해서는 표준 값들(14)을 사용하였다.

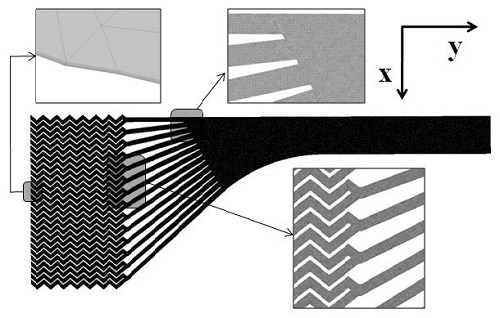
Fig. 1 (10)에 소개된 PCHE의 형상을 기준형상으로 선정하였으며, 본 그림의 PCHE의 전체 형상을 바탕으로 PCHE의 입구부의 형상을 Fig. 2에 나타내었다. PCHE 입구부의 형상은 Fig. 2에서 볼 수 있는 것과 같이 입구부, 입구 파이프 (inlet pipe) 및 지그재그 파이프 (zigzag channel) 등 세 영역으로 나눌 수 있다. Fig. 2에 도시된 PCHE 입구부의 기준 형상 정보를 Table 1 에 제시하였다. 본 연구에서 사용된 기준 형상에 대한 수치모델은 Ishizuka et al.(2)가 연구한 형상 및 경계조건을 기반으로 구축되었다. PCHE 입구부의 수치 해석에 사용된 경계 조건은 Table 2에 제시하였다. 계산영역의 입구에 유량조건이 사용되었으며 출구에 압력조건이 사용되었다. 작동유체는 초임계 이산화탄소(CO₂)가 사용되었으며 초기압력과 초기온도는 각각 8.339 MPa과 110°C 가 사용되었다. Fig. 3에서 보는 바와 같이 대부분의 계산영역에 비정렬 사면체 격자계가 사용되었으며, 벽 근처에서는 정확한 해석을 위하여 경계층 격자로 프리즘 격자계를 사용하였다. 그리고 저 레이놀즈 수 SST모델(low-Reynolds-number SST model)을 사용하기 위해 벽에서 첫 번째 격자점의 위치를 y+ 가 1이하가 되도록 했다.

Fig. 2

Geometry of the inlet part in the PCHE

Fig. 3

Example of grid system in the calculation domain of the inlet plenum in the PCHE

Table 1

Dimensions of the reference geometry of the PCHE.

Table 2

Physical properties and boundary conditions

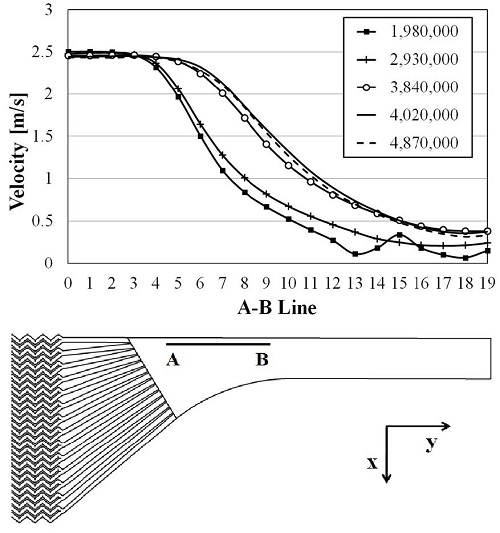
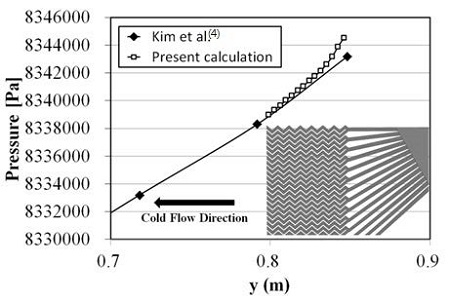
수치모델의 효율성과 신뢰성을 확보하기 위해 격자의존성시험과 신뢰도 검증 시험이 수행되었다. Lee et al.(16)의 선행 연구에서 수행된 격자 의존성 시험 결과를 Fig. 4에 나타내었다. 그래프의 가로축은 아래 그림에 도시한 선분 AB상의 위치를 나타내며 세로축은 선분 AB상의 속도를 나타낸다. Fig. 4에서 확인할 수 있는 바와 같이 격자수가 402만개일 때 격자 의존성이 사라짐을 알 수 있다. 선행연구(16)에서 수행된 수치모델의 신뢰도 검증 결과를 Fig. 5에 나타내었다. 그래프는 입구에서부터의 거리에 따른 각 압력 값들을 나타내고 있다. 그림의 x축은 Kim et al.(4)에 제시된 y좌표 값을 나타내며 PCHE의 입구부분인 0.8 m이후 부분을 취하여 그래프에 나타내었고, 각각의 좌표와 일치하도록 PCHE의 채널 및 입구부의 그림을 삽입하여 표시하였다. 입구에서 멀어지고 후류로 갈수록 유체의 완전 발달 유동이 얻어지면서 기존의 연구 결과(4)와 점차 같아지는 것을 볼 수 있다. 여기서, 삽입된 그림의 위치와 그래프의 위치는 동일하다.

Fig. 4

Results of grid-dependency test

Fig. 5

Validation of numerical results

모든 해석에 있어 지배방정식의 이산화를 위해 고해상도 수치도식(high resolution scheme)이 사용되었으며, 입구 난류강도는 5%로 가정하였다. Residual reduction factor는 10-5로 설정하였을 때 만족스러운 결과 값을 얻을 수 있었다. 한 개의 설계점에 대한 수치모델의 해석을 위해 Intel I7 CPU를 사용하는 컴퓨터에서 8개 병렬코어를 모두 사용하여 약 15시간의 계산시간이 소요되었다.

Fig. 6

Optimization procedure

3. 최적설계기법

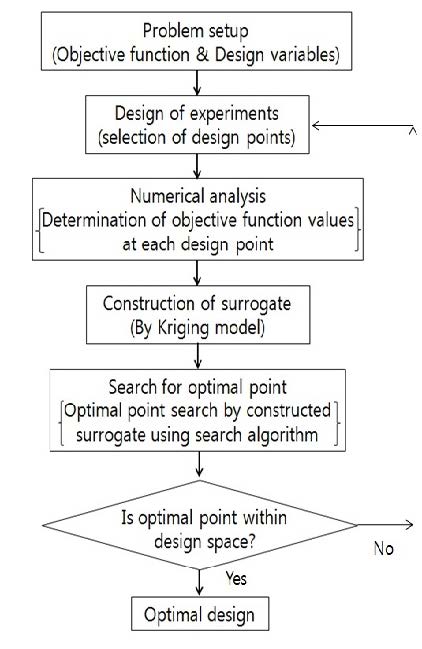
대리모델을 이용한 최적설계의 과정을 Fig. 6에 순서도로 나타내었다. 먼저 목적 함수와 설계변수들을 결정하고, 설계 영역을 선택하게 된다. 이후 LHS을 사용하여 실험점들을 산출 하였다. 이 실험점에서의 유동해석을 통하여 목적함수가 계산되어지고, 이 값들을 바탕으로 KRG방법을 사용하여 대리모델을 구축하게 된다. 이후 최적화 알고리즘을 통하여 대리모델의 자료곡면 상에서 최적점을 찾고 최적점이 설계영역 내에 존재하게 되면 최적화 과정은 종료된다. 만일 최적점의 위치가 설계영역을 벗어나게 되면 수정된 설계영역을 바탕으로 다시 계산을 수행해야 한다.

3.1. 설계변수 및 목적함수

최적설계를 위해서는 설계 변수와 목적함수의 선정이 먼저 되어야 한다. PCHE 입구부의 형상을 최적화하기 위한 설계 변수는 선행 연구(16)로 진행된 형상 변화에 따른 PCHE 입구부의 성능 비교분석 결과를 통하여 Fig. 2에 표시된 입구부 벽면의 각(α) 과 입구부 파이프가 연결된 벽면 길이에 대한 곡률반경의 비(R/L), 그리고 입구부 파이프의 직경과 출구 파이프의 직경의 비(D/D₀) 등, 총 세 개의 무차원 설계변수가 결정되었다. 이 때 D/D₀는 PCHE의 구조적 안정성을 위하여 1.611 이하로 제한 조건을 두었다.

최적설계는 PCHE 입구부를 통한 압력손실계수와 출구부 각 채널 간의 유량의 균일도를 목적함수로 하여 수행되었다. 우선 압력손실계수는 다음과 같이 정의 된다.

위 식에서 P_in은 입구부의 전압, P_out은 출구부의 전압이다. ρ는 냉각 유체로 쓰인 초임계 CO₂의 밀도 값이며, ν_avg는 PCHE 입구부에서의 유체의 평균 속도이다.

유량 분포의 균일도를 나타내기 위하여 출구부의 각 채널들의 유량 m_i 과 출구부 채널 유량들의 평균값 m_avg을 이용하여 무차원화 한 변수를 S_i로 정의하였다. F_f는 이 S_i값들의 표준 편차로 정의하였다.

최종적으로 목적함수 F는 F_f와 F_P를 선형적으로 조합한 식으로 정의하였다.

본 연구에서 최적화의 목적은 F_P와 F_f를 사용하여 정의한 단일함수 F의 최소화에 있으며, β는 최적설계를 위해 유량 균일도와 압력 강하 사이의 비중을 조절하기 위해 사용되는 가중계수로서 설계자에 의해 결정되어 진다.

Table 3

Result of optimization (β = 0.00007)

3.2. 크리깅 모델 (Kriging model)

크리깅 모델은 최적화를 위한 대리모델의 일종으로 Gauss 상관함수를 사용하여 선형 다항식 함수를 사용하여 구축되며, 크리깅의 가정값 F(x)는 식 (5)와 같이 정의된다.

F(x)는 전역모델(global model) f(x)와 이탈(departure) Z(x)의 합으로 나타난다. 여기서 F(x)는 미지의 함수이고, f(x)는 x의 알려진 함수, 즉, 실험점을 통해 구해진 목적함수의 값을 말하며, Z(x)는 평균은 영(zero)이지만 영이 아닌 공분산(covariance)을 갖는 확률적인 과정의 실현, 즉 국부적 분산을 뜻한다. f(x)는 큰 범위의 설계공간을 나타내고 Z(x)는 미소영역의 분산을 나타낸다. 공분산 행렬은 다음과 같이 표현된다.

여기서 N은 설계 변수의 개수이고, x_i와 σ는 모집단의 표준 편차, θ_k는 크리깅 모델을 적용하기 위한 미지의 관계변수이다.

4. 결과 및 검토

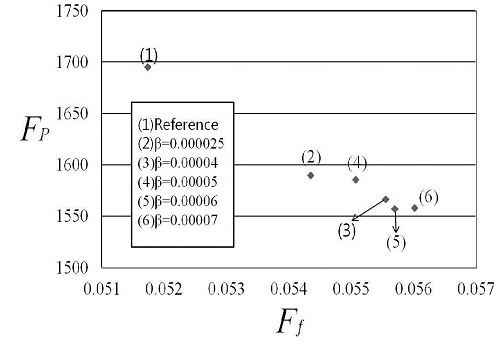
LHS에 의해 선택된 26개의 설계점의 계산 결과를 바탕으로 최적 설계를 수행하였다. 가중계수의 범위, 0.000025∼0.00007에 대해 계산된 최적 설계변수와 목적함수 값을 통해 최적설계 결과를 해석하였다. 가중 계수는 각각의 설계점들에서 계산된 F_P와 F_f의 값들이 비슷한 수치로 표현될 수 있도록 각 평균들의 비를 기준으로 선정하였으며 그 범위를 0.000025∼0.00007로 제한하였다.

Table 3 에 가중 계수가 0.00007인 경우에 대해 계산된 최적 형상과 기준형상에 대한 설계 변수와 목적함수 값을 제시하였다. 최적형상의 목적함수 값은 0.1651로 기준형상의 목적함수 값인 0.1704보다 약 3.23 %정도 감소되었음을 확인할 수 있다. 한편, KRG를 이용하여 예측된 목적함수 값은 0.1599 로 3-D RANS로 해석된 목적함수 값과 비교하였을 때 예측오차 약 3.26 % 로 비교적 정확히 예측되었음을 확인할 수 있다. 균일도 F_f는 0.05174에서 0.05602로 소폭 높아졌지만 압력손실계수 F_P가 1695.36에서 1557.86으로 눈에 띄게 향상된 것을 볼 수 있다.

Table 4와 같이 가중치를 변화시켜 가며 목적함수를 산출 해 낸 결과, 최적화된 목적함수 값들은 KRG 예측 수치 보다 모두 3 % 내외의 작은 오차를 보였으며, 각 가중 계수 별로 0.000025는 0.0266%, 0.00004는 1.14%, 0.00005는 1.61%, 0.00006은 2.91% 0.00007 은 3.23% 향상된 것을 보였다. Fig. 7에 각각의 가중계수 변화에 따라 도출된 최적 형상들의 F_P 와 F_f값을 그래프로 나타내었다. 이를 통하여 가중계수가 변화함에 따라 하나의 함수가 증가하면 다른 함수는 감소하는 관계가 성립함을 확인할 수 있다.

Table 4

Objective function variation with β

Fig. 7

FP and Ff in accordance with weighting factor

Fig. 8

Velocity field inside the inlet part of PCHE

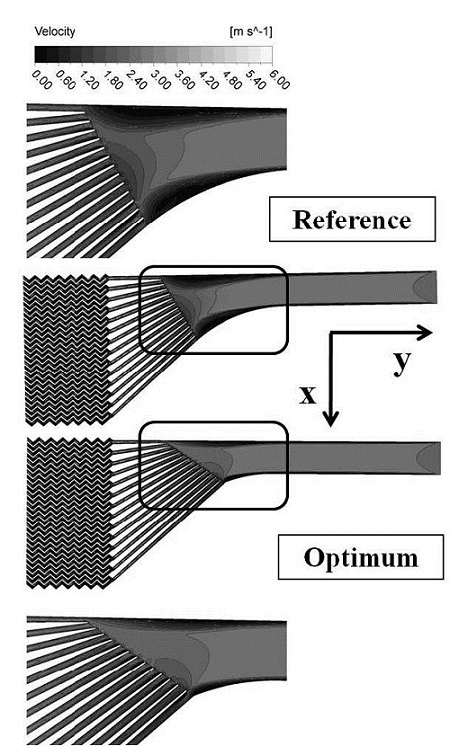
Fig. 8 에 입구부의 속도 분포를 나타내었다. 기준 형상의 입구부 양쪽 부분의 벽에서 유동박리가 크게 나타나는 것을 확인 할 수 있다. Table 3 에 제시된 최적 형상의 속도 분포에서는 에너지 손실을 야기 할 수 있는 유동 박리 영역이 기준 형상에 비해 크게 줄어든 것을 확인 할 수 있다. 이 것이 압력손실이 줄어든 주된 원인이다. 한편, 최적형상은 기준형상에 비해 속도분포가 다소 불균일한 것을 관찰 할 수 있다. 이 것이 최적형상에서 불균일도가 미소하게나마 증가한 원인이 된 것으로 사료된다.

5. 결 론

본 연구에서는 PCHE 입구부의 형상에 대해 RANS 해석과 대리모델인 크리깅모델을 사용해 입구부 내 유량 분포의 균일화와 압력손실을 줄이고자 수치최적설계를 수행하였다. 세 가지 기하학적 설계변수에 대해 LHS기법을 사용하여 26개의 실험점을 선택하였으며, 목적함수는 채널 간 유량의 균일도를 나타내는 인자와 압력손실계수를 가중계수를 사용해 선형결합한 형태로 정의하였다. 임의로 선택된 가중계수에 대해 크리깅 모델로 예측한 목적 함수 값이 3-D RANS 해석을 통한 계산 값과 상대오차 3% 내외로 일치함을 알 수 있었고 기준형상에 비해 3% 이상 향상된 목적함수 값을 얻을 수 있었다. 아울러, 가중계수의 변화에 따른 최적화된 목적함수 값들의 변화를 평가하여 유량 균일도와 압력 손실의 상관관계를 얻어낼 수 있었다.

Acknowledgments

이 논문은 2012년 교육과학기술부의 재원으로 한국연구재단의 지원을 받은 ‘다중현상 CFD연구센터(ERC)’ 의 과제로 수행된 연구임. (NO. 20120000862)

References

• Dewson, S. J., Grady, C., HEATRIC Workshop at MIT, Cambridge, MA, U.S.A, (2003, Oct, 2).
• Ishizuka, T., Kato, Y., Muto, Y., Nikitin, K., Tri, N. L., Hashimoto, H., “Thermal-Hydraulic Characteristics of a Printed Circuit Heat Exchanger in a Supercritical CO₂ Loop”, The 11th International Topical Meeting on Nuclear Reactor Thermal-Hydraulics, Avignon, France paper 218.
• Nikitin, K., Kato, Y., Ngo, L., “Printed Circuit Heat Exchanger Thermal-Hydraulic Performance in Supercritical CO₂ Loop”, International Journal of Refrigeration, (2006), 29, p807-814. [https://doi.org/10.1016/j.ijrefrig.2005.11.005]
• Kim, D. E., Kim, M. H., Cha, J. E., Kim, S.O., “Numerical Investigation on Thermal-Hydraulic Performance of New Printed Circuit Heat Exchanger Model”, Nuclear Engineering and Design, (2008), 238, p3269-3276. [https://doi.org/10.1016/j.nucengdes.2008.08.002]
• Ngo, L., Kato, Y., Nikitin, K., Tsuzuki, N., “New Printed Circuit Heat Exchanger with S-shaped Fins for Hot water Supplier”, Experimental Thermal and Fluid Science, (2006), 30(8), p811-819. [https://doi.org/10.1016/j.expthermflusci.2006.03.010]
• Pra, F., Tochon, P., Mauget, C., Fokkens, J., Willemsen, S., “Promising designs of compact heat exchangers for modular HTRs using the Brayton cycle”, Nuclear Engineering and Design, (2008), 238, p3160-3173. [https://doi.org/10.1016/j.nucengdes.2007.12.024]
• Kim, I. H., No, H. C., Lee, J. I., Jeon, B. G., “Thermal-hydraulic Behavior in a Deteriorated Turbulent Heat Transfer for a Gas-Cooled Reactor”, Nuclear Engineering and Design, (2010), 240, p783-795. [https://doi.org/10.1016/j.nucengdes.2009.11.004]
• Oh, C. H., Kim, E. S., Sherman, S., Kim, J. H., No, H. C., “ Application of Gamma Code Coupled with Turbomachinery Models for High Temperature Gas-Cooled Reactors”, The 12th International Symposium on Transport Phenomena and Dynamics of Rotating Machinery(ISROMAC12), ISROMAC12-2008-20224, (2008.).
• Lee, S. M., Kim, K. Y., “A Parametric Study on Fluid Flow and Heat Transfer in a Printed Circuit Heat Exchanger”, Proceedings of the ASME/JSME 2011 8th Thermal Engineering Joint Conference(AJTEC2011), AJTEC2011-44629, (2011.).
• Southall, D., Le Pierres, R., Dewson, S. J., “Design considerations for compact heat exchangers”, Proceedings of ICAPP ’08, Anaheim, CA, USA, Paper No. 8009, (2008.).
• Sacks, J. W., Welch, J., Mitchell, T. J., Wynn, H. P., “Design and analysis of computer experiments”, Statistical Sci, (1989), 4(4), p409-435. [https://doi.org/10.1214/ss/1177012413]
• Mckay, M. D., Beckman, R. J., Conover, W. J., “A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code”, Technometrics, (1979), 21, p239-245.
• CFX-11.0 Solver Theory, Ansys inc, (2008.).
• Menter, FR., “Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications”, AIAA Journal, (1994), 32, p1598-1605. [https://doi.org/10.2514/3.12149]
• Bardina, J. E., Huang, P. G., Coakley, T., “Turbulence Modeling Validation”, 28^th AIAA Fluid Dynamics Conference, Snow Village, CO, USA, AIAA paper, (1997), p1997-2121. [https://doi.org/10.2514/6.1997-2121]
• Lee, S. M., Koo, G. W., Kim, K. Y., “Parametric study on hydraulic performance of an inlet plenum in a printed-circuit heat exchanger”, 5^th International Symposium on Fluid Machinery and Fluids Engineering (ISFMFE 2012), 32-3, (2012.). [https://doi.org/10.1007/s11431-013-5294-2]