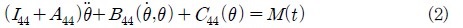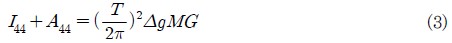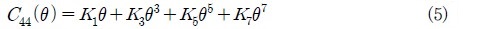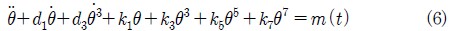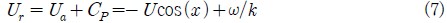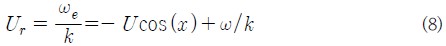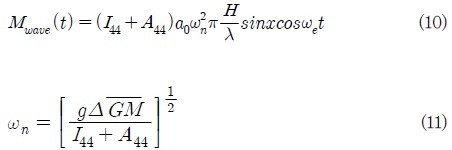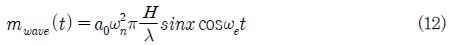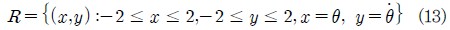Probability Prediction of Stability of Ship by Risk Based Approach

1. 서 론

최근 다양한 방법에 의한 선박의 복원성 연구가 많은 연구자들에게 관심을 받고 있다. 선박의 복원성은 해양에서의 생명의 안전과 직결되기 때문에 매우 중요한 요소이다. 그리고 선박의 불안정성(Unstable) 및 전복(Capsizing)은 해양에서 선박의 극한적 거동에 관련된 매우 드문 현상으로 간주되기도 있다. 하지만 그 현상에 의한 최종 결과는 매우 치명적이다. 극한 해상 상태에서 전복에 대항하는 안정성은 선박 설계시 고려되는 가장 기본적인 요구사항 중에 하나이다(1^~5). 또한 선박의 전복에 대한 기본적인 연구목적은 극한 해상 상태에서의 선박 거동을 이해하고 비용절감과 안전 운행을 위하여 선박의 형상 및 기능적 특성과의 관련성을 알아보는 데 있다. 한편, 초기 복원성 규약의 개정은 2001년에 시작되었다. 그리고 그 첫 단계로서 중요한 구조적 재편성과 실험적 기반에 대한 대체방법의 개발이며 이것은 기존 영역 외의 변수들을 가지는 선박의 환경조건에 대한 요구사항들을 수렴하기 위한 것이다. 또한, 이 규약은 2006년(6)에 완성되었고 2009년에 SOLAS 협정의 조항아래 의무적으로 될 것이다.

2. 선박 복원성의 위험도 기반 접근법

선박의 복원성 시스템은 상당히 복잡하다. LOSA(Loss Of Stability Accident) 사고들의 분석결과에 의한 사고원인이 기능적 측면, 운용적 측면, 외부적 원인들의 결과 또는 화물 관련 측면에 기인할 수도 있다고 밝히고 있다(7).

2.1. 파랑의 힘에 대한 복원성 기준

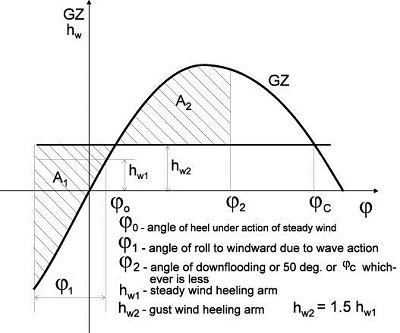
해양파랑에 노출된 위험요소들은 LOSA와 전복의 안전성에 매우 큰 영향을 미치는 위험한 요소이다. 본 논문은 IS 규약을 바탕으로 한 복원성 기준에 주안점을 두었으며 환경기준(weather criterion)내에서 파랑의 힘을 고려한 규약은 기존에 이미 A.562(8) 결의에 의해서 채택되었다. 한편, 횡방향의 바람과 횡요의 결합된 효과에 견디는 선박의 능력은 Fig. 1을 참고로 한 다음의 파랑하중에 대한 각각의 표준 조건에 따라야 한다.

1) 선박은 정상풍의 횡경사 길이 h_ω1의 결과인 선박 중심선에 수직으로 작용하는 정상 풍압력에 지배된다.

2) 선박은 정상풍에 기인한 횡경사각 ø₀ 근방의 파도에서 횡동요(Rolling)한다. 횡동요의 진폭은 바람불어오는 쪽을 향한 ø₁과 동일하다. 정상풍에 기인한 경사각은 16도 또는 갑판침수각의 80% 중 어느쪽이든 더 작은 것 보다 크지 않아야 한다.

3) 선박의 이러한 상황에서 동적 바람 경사모멘트 h_ω2에 지배된다.

4) Fig. 1에서 면적 A₂는 면적 A₁으로부터 더 크거나 같게 되어야 한다.

환경기준(weather criterion)이 포함된 IMO 초기 복원성 규약은 기존에 건조된 선박과 선체 파라메타들에 존재하는 것을 기반으로 한 간단한 기준이다. 그리고 그것은 지금의 설계기준과 다소 다르다. 따라서 위험도 해석의 적용이 기존의 복원성 기준에 대한 개선안으로서의 큰 역할을 수행할 것으로 사료된다.

Fig. 1

Weather criterion as in the IS Code

2.3. 전복 확률 평가

어떤 사고 또는 파손 가능성의 종합 지수로서 정의되는 위험도(Risk)로 인하여 재산손실과 그에 따른 결과들이 수반되기 마련이다(10^~12). 그리고 가장 주요한 시나리오상의 위험요소들이 이전단계에서 식별된 후에 그 발생 가능성과 모든 위험 결과들을 분석하게 된다. 그리고 전체 위험지수가 확률과 결과지수들에 의한 식이 다음과 같이 수립될 수 있다.

P_i는 주어진 위험의 발생 확률 지수이다. C_i는 환경에서의 재산 손실과 피해, 손상, 재난에 대한 항들로서 데이터 위험과 시나리오 개발의 발생에 따른 결과지수들이다.

항해기간동안 전복가능성이 계산된다면, 연속되는 연간 전복 가능성이 계산될 수 있으며 동일한 접근법에 의해 선박의 수명기간 동안 전복 가능성을 결정하는데 사용되어 질 수 있다.

3. 횡동요의 이론배경과 방정식

Surge와 Heave 그리고 Pitch에 대한 Roll의 1차 연성(The first-order coupling)은 없으며, Sway와 Yaw의 Roll에 대한 연성(Coupling)은 선박이 좌우현 대칭이므로 고려하지 않는 것으로 가정한다. 횡파에서 선박의 1자유도 횡동요 미분 방정식은 일반적으로 다음과 같다(13)(14).

I₄₄는 횡동요축에 대한 선박질량의 관성모멘트 계수이다. A₄₄는 부가질량의 유체역학적 관성모멘트 계수이다. B₄₄는 유체역학적 감쇠계수, C₄₄는 유체정역학적 선박의 복원 모멘트, M(t)는 기진력(파와 바람 외력을 포함) 그리고 θ는 선박의 횡요각을 나타낸다. 여기서,

T는 선박 횡요 주기, ∆g는 부력, MG는 메타센타 높이를 의미한다. 그리고 비선형항은 일반적으로 다음과 같이 표현한다.

복원 모멘트는 유체정역학적이며 비선형 기함수로서 주어진다. 그리고 5차 다항식에 의해 다음과 같이 표현될 수 있다.

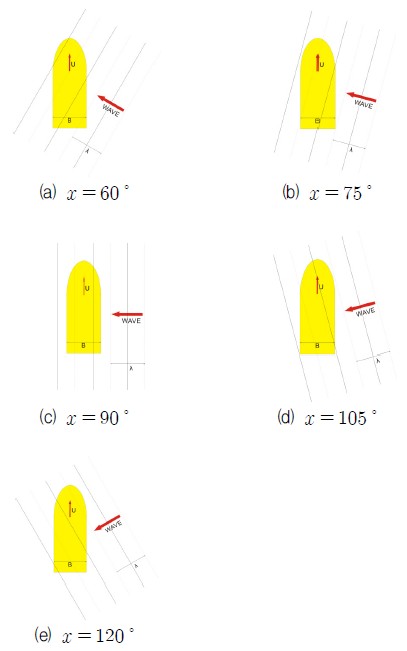
윗식 (4), (5)를 식(2)에 대입하여 관성 가상 모멘트에 의한 값으로 나누면 운동 미분방정식의 최종 방정식은 다음과 같이 얻어진다.

여기서,

d_i = D_i/(I₄₄ + A₄₄)     i = 1,3

k_i = K_i/(I₄₄ + A₄₄)     i = 1,3,5,7

m(t) =M(t)/(I₄₄ + A₄₄)

4. 극한환경에서의 동적 복원성 평가

4.2 선박과 파랑의 조우주파수

파랑의 회두각은 선박진행 방향과 파속 C로 전달되어 오는 파 방향 사이의 각으로 정의 된다. 파향은 정확한 횡파(x = 90°) 근방으로 변화된다. Fig. 2에서 보는 바와 같이 60°와 120°사이의 변화되는 회두각 x를 생각한다. 선박 속도는 0 m/s, 1m/s, 2m/s, 3m/s 그리고 4 m/s로 하며 프루드 수(F_N, Froude number)은 0, 0.11, 0.22, 0.34, 0.45로 나누어 모사하였다.

Table 1

Parameters of the analysed ship

Table 2

Coefficient of relative restoring moment

Fig. 2

Definition of heading angle

선박이 움직일 때 선박의 운동은 선박위의 탑승자의 시각에서 입사파의 방향에 영향을 미친다. 파랑이 어떤 각도 x로 입사하여 온다면 그때 파 전달방향에서 선박의 속도 성분은 U_a = -U × cos(x)가 된다. 파곡들은 위상속도 C_P = ω/k와 선박과 파랑 사이의 상대속도에서 움직인다. 여기서 ω는 각주파수이고 k는 파수를 의미한다.

그때 파랑은 다음과 같은 위상속도를 가진다.

심해에서의 파랑의 분산관계식을 사용하여, 다음과 같이 조우주파수 방정식을 다시 쓸 수 있다.

4.3 해양파로부터의 기진 모멘트

규칙파로부터 외부 기진 모멘트는 조화 정현함수에 의해 근사화될 수 있다. 이것은 다음 식으로 나타낼 수 있다(16).

Fig. 3

Probability of wave height and steepness

a₀는 유효 파형경사 계수이고, ω_n은 초기 횡요 고유 주파수, 은 선박의 메타센타 높이이다. H는 파고, λ는 파장이고, ω_e는 조우 주파수이다. 기진력 식(10)은 부가관성모멘트 I₄₄ + A₄₄의 유효횡요관성으로 나누어진다.

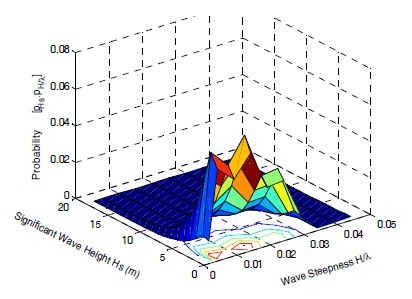
a₀는 유효 파형경사 계수이고, 이것은 상수 0.729(17)를 취하고 ω_n과 ω는 각각 1.32 rad/s 과 3 rad/s과 동일하게 한다. 유의파고 H_1/3 = 5m와 파장λ의 항은 유의파고와 파형 경사의 분포를 나타내는 Fig. 3과 같이 확률분포에 따라 선택될 수 있다 (18)(19).

5. 계산결과와 고찰

조화 기진력에서 초기 선박의 전복과 횡동요 계산에 대하여, 비선형 동적 시스템의 안전영역이 위상궤적공간에서 경계영역 A를 사용하여 정의될 수 있다. 안전영역(Safe Basin)으로부터 시작하는 궤적은 영역 A를 유지하게 된다. 시간 t가 무한할 때, 안전영역을 넘어 시작한 궤적은 불안전한 영역 A를 벗어나려 할 것이다. 그리고 결국 그 시스템이 붕괴되고 파괴될지도 모른다. 따라서, 안전영역의 모양과 범위가 시스템 변수의 변화로 인해 함께 변화가 일어나게 될 것이다.

5.1. 계산결과

안전영역에 의한 평가가 수치적으로 연구되었다. 기진력이 변화하였을 때 그리고 다른 변수들이 상기의 고찰로부터 선택될 때, 둘러싸여진 영역 A는 다음과 같이 정의된다(20).

이때 영역 A는 80 × 80의 격자모양으로 나누어진다. 그리고 격자점은 시스템의 해에 대한 초기값으로서 취해진다. 그리고 여기서 x는 횡요각, y는 횡요각속도를 의미한다.

시스템의 해는 충분히 긴 t = 2000s에 대한 영역 R로 유지된다. 그 해는 근사적으로 안전영역으로 취해질 수 있다. 그리고 교차하는 격자는 안전영역의 일부분으로서 취해진다. 만일 시스템 해가 영역 A를 피한다면 그러한 해는 불안전 해를 취하게 된다. 그리고 그 교차격자는 안전영역 넘어 존재한다. 전체 지배 방정식은 수치적으로 4차 Runge-Kutta algorithm에 의해 적분된다. 그리고 수치적 결과는 다음과 같이 보여준다.

Fig. 4

Erosion of safe basin (V = 4m/s, 회두각=60°)

Table 3

Coefficients of the excitation moment

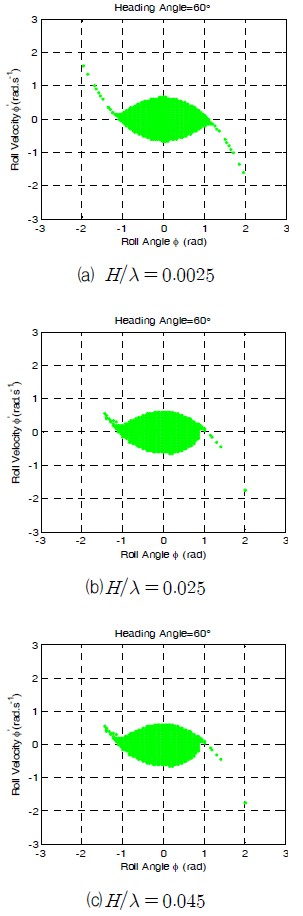
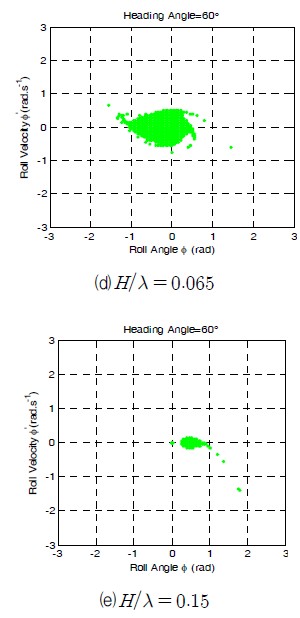
파형 경사의 분포에 따라 0.015, 0.025, 0.045, 0.065 그리고 0.15로서 선택되었다. 회두각은 60°로 하였으며 기타 제원은 Table 3와 같다. 여러 다른 경사각에서 안전영역의 감소는 Fig. 4에서 나타난 것과 같다. 영역내에서 검은 지역은 불안전한 영역을 나타내고 있다.

계산결과들은 H/λ = 0.0025(Fig. 4(a))일때의 경우에서 있어서 안전영역 경계가 어떠한 감소도 없이 매끄러움을 보여준다. 파형경사가 H/λ > 0.0025일 때, 안전영역은 Fig. 4(b)와 같이 경사값이 증감하면서 점차적으로 줄어든다. 그리고 H/λ = 0.15일 때, Fig. 4(e)와 같이 안전영역은 거의 사라진다. 따라서, 파형경사 0.0025와 0.15는 점차 줄어드는 과정에 대한 두 개의 중요한 임계점을 나타낸다.

References

• McTaggart, K. A., "Wind effects on intact ship stability in beam seas”, Journal of Wind Engineering and Industrial Aerodynamics, (1992), 44(1), p2487-2498. [https://doi.org/10.1016/0167-6105(92)90040-H]
• Taylan, M., "Static and dynamic aspects of a capsize phenomenon”, Ocean Engineering, (2003), 30(3), p331-350. [https://doi.org/10.1016/S0029-8018(02)00027-6]
• Konovessis, D., Vassalos, D., "Risk-based design for damage survivability of passenger Ro-Ro vessels”, IOS Press 54, (2007), p129-144.
• Mamontov, E., Naess, A., "An analytical-numerical method for fast evaluation of probability densities for transient solutions of nonlinear stochastic differential equations”, International Journal of Engineering Science, (2009), 47(1), p116-130. [https://doi.org/10.1016/j.ijengsci.2008.08.001]
• Neves, M. A. S., Rodriuez, C. A., "A coupled non-linear mathematical model of parametric resonance of ships in head seas”, Applied Mathematical Modelling, (2009), 33(6), p2630-2645. [https://doi.org/10.1016/j.apm.2008.08.002]
• Francescutto, A., "The Intact Ship Stability Code Present status and future developments", (2007.).
• Kobylinski, L., "Stability and safety of ships: holistic and risk approach”, Reliability & Risk Analysis: Theory & Applications, (2008), 1(1), p11-16.
• IMO, "Recommendation on Resolution A.562(14) Research Project", (1987.).
• Kobylinski, L., “Stability of ships: risk assessment due hazards created by forces of the sea”, Hydronav 2007 Intern. Conference, (2007), p51-62. [https://doi.org/10.1016/S1644-9665(12)60265-9]
• Ben, Webster., R. Sampson, “Suitability of Stability Criteria Applied to Small Fishing Vessels and Associated Survivability”, Research Project 557. Session A, (2006.).
• Paik, J. K., Thayamballi, A. K., “Ship-shaped offshore installations: design, building, and operation”, New York, Cambridge University Press, (2007.).
• Iqbal, K., Bulian, G., “A rational analysis of intact stability hazards involving small inland passenger ferries in Bangladesh”, Journal of Marine Science and Technology, (2008), 13(3), p270-281. [https://doi.org/10.1007/s00773-008-0016-3]
• Wright, J. H. G., Marshfield, W. B., “Ship roll response and capsize behaviour in beam seas”, Transactions, Royal Institution of Naval Architects, (1980), 122, p129-148.
• Lee, S. K., Surendran, S., “Roll performance of a small fishing vessel with live fish tank”, Ocean Engineering, (2005), 32(14), p1873-1885. [https://doi.org/10.1016/j.oceaneng.2004.11.011]
• Marta PEDISIC BUCA AND SENJANOVIC, I, “Nolinear ship rolling and capsizing," BRODO GRANDJA, (2006), 57(4), p321-331.
• Senjanovic, I., Cipric, G., “Survival analysis of fishing vessels rolling in rough seas”, Philosophical Transactions: Mathematical, Physical and Engineering Sciences, (2000), 358(1771), p1943-1965. [https://doi.org/10.1098/rsta.2000.0622]
• Gu, J. Y., “Nonlinear Rolling Motion of Ship in Random Beam Seas”, Journal of Marine Science and Technology, (2004), 12(4), p273-279.
• Soliman, M.S., Thompson, J. M. T., “Transient and steady state analysis of capsize phenomena”, Applied Ocean Research, (1991), 13(2), p82-92. [https://doi.org/10.1016/S0141-1187(05)80065-3]
• McTaggart, K. A., "Capsize Risk Assessment Using Fredyn Ship Motion Predictions Technical Memorandum", (1999.).
• Lee, S. K., Long, Z. J., "Risk assessment method of simulation-based for the intact ship stability”, International Conference on Computational & Experimental Engineering and Sciences(ICCES'09), Phuket, Thailand, (2009), p20-28.