소규모 플랜트 기자재의 고장밀도함수가 가용도에 미치는 영향 평가

1. 서 론

플랜트는 공정계통상에서 속성상 누설, 점화, 부식, 침착 등 다양한 현상을 보이며, 특히 유틸리티의 공급과 처리를 위한 시설의 대형화에 따라 사고나 기능 상실 등 위험도 또한 크게 증가하여 기능유지를 위한 안정성과 신뢰성 확보가 매우 중요시되고 있다.^(1-2)

복잡성을 갖는 대규모 플랜트 시스템의 운영에 있어서 생산성은 생애주기 비용에 미치는 영향이 매우 크며, 이는 플랜트 공정계통 설계의 주요한 이슈로 자리매김하고 있다. 이러한 생산성 설계에 큰 영향을 미치는 평가항목으로 가용도(availability)가 설계에서 차지하는 비중이 증가하고 있다.

가용도에 관한 주요 연구동향을 살펴보면, Komal 등이 시스템의 신뢰성, 가용성 및 유지보수성 분석은 설계수정, 필요시 최적 성능을 얻기 위해서 중요한 역할을 할 수 있으나 유효한 정보나 불확실한 데이터를 이용함에 따라 원하는 수준의 정확도를 달성하는데 변수 추정의 어려움이 있음을 파악하였다.⁽⁵⁾

Sharma 등은 시스템의 신뢰성, 가용성 및 유지보수성 분석방법이 최소 고장 또는 필요시 평균고장간격을 증가시키거나 신뢰성을 최적화, 가용성을 극대화, 유지보수를 계획하는 등 설계 수정을 수행하는데 효과적임을 제언한 바 있다.⁽⁴⁾ Borgonovo 등⁽⁵⁾은 플랜트 유지보수전략과 운영절차의 평가를 위한 몬테카를로 시뮬레이션 기법이 다양한 분석모델에 의해 파악되지 않은 플랜트 관리, 노후, 복구 등 유지보수 및 운영을 위한 유연한 도구로 활용될 수 있음을 보였다.

본 논문은 비교적 단순한 공정계통을 갖는 플랜트의 가용도 시뮬레이션 방법론의 적합성에 관한 연구로서, 도입된 가용도 해석이론 및 시뮬레이션 기법을 소규모 플랜트 시범모델에 적용하여 결과의 신뢰성을 고장밀도함수, 장치의 수, 반복계산 횟수 등에 따라 비교 및 평가하였다.

2. 가용도 시뮬레이션 모델

2.1 시뮬레이션 모델링

플랜트는 복잡한 단위공정과 기자재, 유틸리티의 집합으로 구성되며, 공정 및 모듈 구성 등에 따라 효율과 용량, 안전성, 경제성 등이 영향을 받는다. 이러한 영향은 이상적인 설계조건 하에서 어느 시점에서도 만족스럽게 운전될 수 있는 확률로 설명할 수 있으며, 이는 실제운전시간과 고장이 없이 이상적인 연속운전시간과의 비로 나타낼 수 있다.

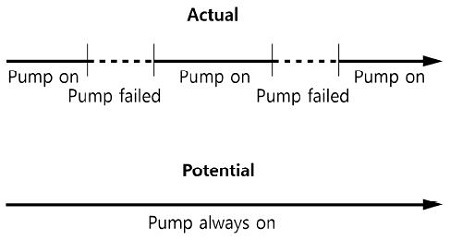
Figure 1에 도시한 바와 같이 펌프가 고장이나 수리시간이 없이 연속적으로 작동하여 이상적인 운전이 가능한 시간을 가정하고, 주어진 환경과 운전조건 하에서 실제 운전되는 시간을 산정할 수 있으며, 이들의 비를 가용도로 정의한다.

Fig. 1

The concept of availability.

플랜트를 부품이나 장비의 신뢰성은 MTTF (mean time to failure)라는 용어로 나타내며, 사용 중에 수리하지 않는 비수리계 기기나 장비가 작동을 시작하여 고장이 날 때까지 평균시간을 말한다.

다수의 장치로 구성되어 고장시 수리하여 정상운전인 가능한 수리계는 MTBF(mean time between failure)를 신뢰성 표현으로 사용하는데 고장 간 평균시간을 의미한다. 또한 보전성의 척도이면서 가용도를 계산하기 위한 변수인 MTTR(mean time to repair)은 평균수리시간을 의미한다.

생애주기 동안 수리(repair)를 통하여 운전되는 시스템의 경우에 고장이 일어나는 평균적인 시간간격(MTBF: mean time between failure)과 이러한 고장률에 따라 평균적인 보전(수리)시간(MTTR: mean time to repair)을 산정한다.

이러한 정의를 이용하면 플랜트나 시스템의 잠재 운전시간은 MTBF(mean time between failures)와 MTTR(mean time to repair)의 합으로 계산될 수 있다. 실제 운전시간은 파손 또는 고장(failure)이 일어나는 시간간격인 MTBF이므로 가용도는 식 (3)과 같이 나타낼 수 있다.

$\[ \mathrm{Availability}=\frac{\mathrm{MTBF}}{\mathrm{MTBF}+\mathrm{MTTR}} \]$

(1)

2.2 고장이벤트

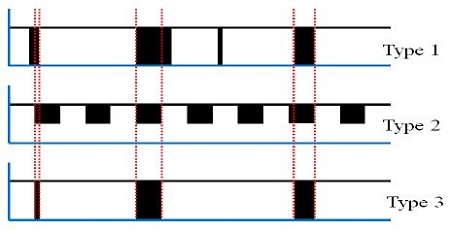
플랜트는 수많은 장치류, 단위공정, 기자재 등으로 구성되므로 다양한 유형의 고장 현상과 수리기간 등을 가지므로 근본적으로 불확실성(uncertainty)을 가지고 있다. 이러한 불확실성을 고려하여 시스템에서 일어날 수 있는 다양한 생애주기 이벤트를 가정할 수 있으며, Fig. 2에 도한 바와 같이 비계획, 계획, 이들의 조합에 의한 세 가지 유형의 고장 이벤트를 가정할 수 있다.

Fig. 2

Basic types of failure event

비계획적인 이벤트 생성은 불규칙적으로 발생하며 보통은 특별한 수학적 분포함수를 따르는 형태로 나타난다. 이러한 유형은 주로 시스템내의 장비 고장을 수반하는 경우이다. 반대로 계획적인 고장 이벤트 생성은 수명주기 등이 알려져 있는 경우로 가속수명시험, 장비의 일정한 검사나 점검 등을 통하여 확인할 수 있다.

계획 및 비계획적인 방법의 조합에 의한 고장 이벤트 생성은 개별 고장이벤트와 시스템 고장 이벤트 그룹간의 의존성을 나타낼 수 있는 장점을 가지고 있다. 일반적인 설계⋅생산된 제품의 경우 적절한 수명주기를 가지나 일부 우발적인 고장 이벤트를 고려할 수 있다.

이러한 생애주기 고장 이벤트 생성기법을 가정하여 플랜트를 구성하는 모든 시스템 및 부품, 기자재에 대하여 확률적으로 조합이 가능한 이벤트의 시나리오에 의하여 전체 시스템의 운전 스케쥴은 Fig. 3와 같이 다양하게 생성된다.

Fig. 3

Schematic diagram of system event

또한 고장이 발생하여 운전이 부분 또는 완전 중단되면 조치를 위한 상황파악, 재고부품 확인 또는 발주, 수리활동 등에 시간이 소요되고 수리가 완료된 후에도 정상가동에는 일정한 시간이 소요되므로, 이 때 필요한 시간을 보전에 필요한 시간을 다운타임(down time)으로 반영한다.

3. 결과 및 고찰

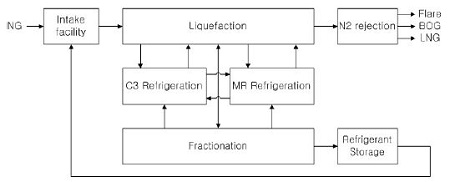
상기 설명한 적용기법을 이용하여 Fig. 4와 같이 소규모 플랜트 시스템을 구성하는 공정계통에 대한 기자재 목록별 OREDA(2009) 고장율을 적용하여 다음과 같은 결과를 도출하고 고찰을 수행하였다.

Fig. 4

Configuration of small-scale plat for availability simulation

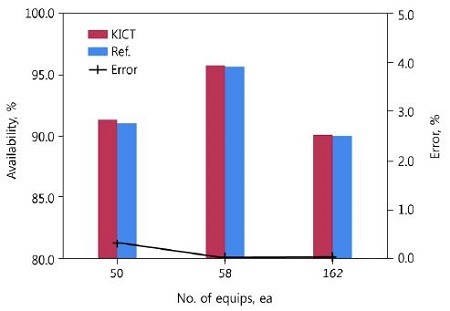
Figure 5와 6 및 7은 기자재의 고장밀도함수가 각각 지수분포, 정규분포, 와이블분포를 따르는 경우에 KICT 및 상용 프로그램에서 기자재수에 따른 가용도 차이를 비교한 것이다. 이 때 프로그램 간 가용도 차이 비교는 차이값을 기준 프로그램에서 계산된 가용도 값으로 나누어 계산하였다.

Fig. 5

Comparison of availability with number of equipment for the case of exponential function

Fig. 6

Comparison of availability with number of equipment for the case of normal function

Fig. 7

Comparison of availability with number of equipment for the case of Weibull function

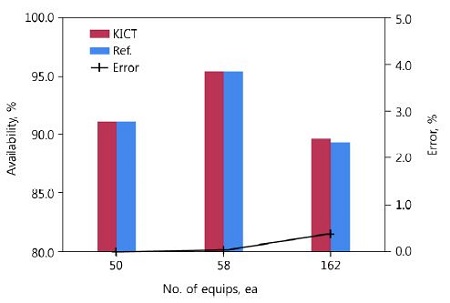
Figure 5는 기자재의 고장밀도함수가 지수분포를 따르는 경우로서 기자재수가 50개인 경우의 각각의 가용도는 91.39%와 91.13%로, 기자재수가 58개인 경우의 각각의 가용도는 95.66%와 95.63%로, 기자재수가 162개인 경우의 각각의 가용도는 90.05%와 90.02%로 계산되었다.

이 경우에 두 프로그램의 가용도 값은 기자재수가 50개인 경우에 0.26% 이하, 기자재수가 58개인 경우에 0.03% 이하, 기자재수가 162개인 경우에 0.03% 이하로 평가되었다.

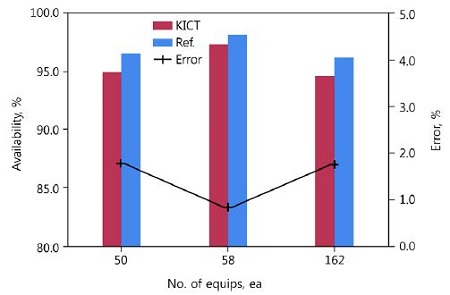
Figure 6은 기자재의 고장밀도함수가 정규분포를 따르는 경우 기자재수에 따른 비교 결과이다. 기자재수가 50개인 경우 각각의 가용도는 94.86%와 96.56%로, 기자재수가 58개인 경우 각각의 가용도는 97.29%와 98.12%로, 기자재수가 162개인 경우 각각의 가용도는 94.60%와 96.25%로 계산되었다. 이 경우에 두 프로그램에서 가용도 값은 기자재수가 50개인 경우에 1.7% 이하, 기자재수가 58개인 경우에 0.83% 이하, 기자재수가 162개인 경우에 1.65% 이하로 평가되었다.

Figure 7은 기자재의 고장밀도함수가 와이블분포를 따르는 경우 기자재수에 따른 비교 결과이다. 기자재수가 50개인 경우 각각의 가용도는 91.11%와 91.12%로, 기자재수가 58개인 경우 각각의 가용도는 95.49%와 95.53%로, 기자재수가 162개인 경우 각각의 가용도는 89.73%와 89.41%로 계산되었다. 이 경우에 두 가지 프로그램에서 가용도 차이는 기자재수가 50개인 경우에 0.01% 이하, 기자재수가 58개인 경우에 0.04% 이하, 기자재수가 162개인 경우에 0.32% 이하로 평가되었다.

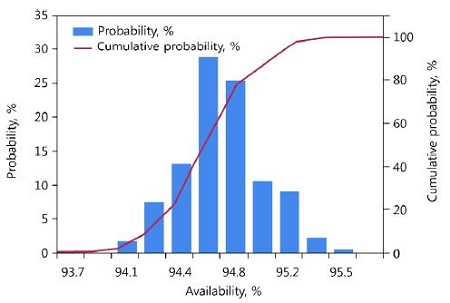
Figure 8은 몬테카를로 시뮬레이션에 기초한 가용도 분석결과를 히스토그램으로 도시한 결과이다. 정규분포를 가지는 고장밀도함수를 가정한 경우에 250회 반복 수행을 하였을 때 확률밀도함수는 막대그래프로 도시되어 정규분포의 가정을 추종하고 있다. 그림에서 실선으로 표기된 누적분포함수 또한 정규분포의 특성을 반영하고 있다. 이는 통계적으로 95% 신뢰수준과 ±0.3% 오차범위를 제시하고 있다.

Fig. 8

Histogram of availability results

4. 결 론

이상과 같이 복잡한 공정계통을 갖는 플랜트의 가용도 시뮬레이션 방법론의 적합성에 관한 연구를 수행하여 다음과 같은 결론을 도출하였다.

적용 기자재의 복잡성에 따른 가용도 비교결과에서 고장밀도함수가 정규분포를 따를 경우의 가용도 차이는 최대 1.7% 수준을 보였으나 다른 모든 경우에는 매우 낮은 차이를 보여 적용성에 문제가 없는 것으로 평가되었다.

반복 수행 횟수에 따른 가용도 차이는 정규분포함수에서 100회 계산시에 2.0% 수준의 최대값을 보이고 나머지 분포함수에서는 소수점 이하의 차이를 보이고 있다.

반복횟수의 적용에 있어서 시스템의 복잡성과 고장빈도에 따른 이벤트 수에 따라 반복횟수는 다르게 적용되나 시스템 구성이 단순한 경우에도 충분한 경우의 수를 반영하기 위해서는 250회 이상의 반복횟수가 바람직하다.

Acknowledgments

본 연구는 국토교통부 플랜트연구개발사업의 연구비지원(15IFIP-B089069-02)에 의해 수행되었습니다.

References

• Barten, H. J., and Scheurenbrand, J. A., (1971), “Stress and Vibration Analysis of Turbopump Inducer Blades by Finite Elements”, Journal of Spacecraft, 8(6), p657-664. [https://doi.org/10.2514/3.59707]
• Kang, K. W., Yoon, M. O., Lee, H. C., and Hwang, I. J., (2012), “A study on the availability with failure rate of process for LNG plant”, KJACR, 24(4), p358-363. [https://doi.org/10.6110/kjacr.2012.24.4.358]
• Komal, Sharma, S. P., and Kumar, D., (2010), “RAM alanysis of repairable industrial systems utilizing uncertain data”, Applied Soft Computing, 10, p1208-1221. [https://doi.org/10.1016/j.asoc.2009.12.019]
• Sharma, R. M., and Kumar, S., (2008), “Performance modeling in critical engineering systems using RAM analysis”, Reliability Engineering and System Safety, 93, p891-897. [https://doi.org/10.1016/j.ress.2007.03.039]
• Borgonovo, E., Marseguerra, M., and Zio, E., (2000), “A Monte Carlo methodological approach to plant availability modeling with maintenance, aging and obsolescence”, Reliability Engineering and System Safety, 67, p61-73. [https://doi.org/10.1016/S0951-8320(99)00046-0]