Operational Vibration Experiment and Analysis of a Small Vertical-Axis Wind Turbine Considering the Effect of a Tower Stiffness

1. 서 론

현재 세계적으로 나타나고 있는 지구온난화 등의 이상기상현상에 대한 우려 속에 가장 실용적인 대안으로 인정받고 있는 분야는 풍력발전이다. 화석연료와 같이 기존에너지원과는 다르게, 무한 무공해 에너지인 바람을 동력원으로 한다는 장점을 가지고 있다. 독일 등 유럽 선진국을 선두로 발전하고 있는 풍력 발전 사업은 미국의 환경 친화적인 그린뉴딜정책과 맞물린 유망사업으로 부각되어 연구와 개발이 더욱더 활발히 이루어지고 있는 실정이다. 국내에서도 이러한 흐름에 맞춰 저탄소 녹색성장 정책 등 풍력 발전에 대한 개발과 지원이 국가차원에서 진행되고 있으며, 풍력발전기에 대한 연구개발 중에서 대기업을 중심으로 한 대형풍력발전 분야 또한 급성장하고 있다.(1)

풍력발전시스템의 상업적 보급은 1990년대 중반 이후 본격적으로 이루어지게 되었고, 2008년 말 세계 누적 풍력설비용량은 대략 122 GW 에 달하고 있다. 풍력시장의 확대와 함께 유사한 추이로 상업용 풍력발전시스템의 단위 용량 규모도 1980년대 초의 50 kW 급에서 현재 6 MW 급으로 120배 커졌다. 이러한 국제시장의 확대와 신규설비 교체 수요에 따른 리파워링(repowering), 해상용 풍력발전(offshore wind power)설비가 증가할 것이라는 예측과 함께 풍력발전기의 개발형태도 다양해지고 있다.

풍력발전기가 점점 대형화됨에 따라 이를 제작하는 비용도 급격히 증가하고 있는 상황이다. 어떻게 저비용 고성능 풍력발전기를 제작할 수 있을지에 대한 고민은 모든 풍력발전기를 개발하는 모든 국가, 기업들의 숙제와 같다. 그리고 국내의 경우, 풍력발전기를 실제 성능 테스트 검증을 통해 시행착오를 겪으면서 설계 제작할 수 있는 연구비가 충분하지 않다. 이에 최대한 적은 시행착오를 겪기 위해서 FEM 해석의 정확성은 확실히 검증되어야 한다.

본 논문에서는 풍력발전기용 타워를 소형풍력발전기에 체결한 후 지상 풍동 베이스에 설치하고 송풍기를 이용하여 가진 응답 실험을 수행하였다. FEM 진동해석결과를 바탕으로 공진 RPM에서의 가속도와 변형률을 분석하고 전산 다물체 동역학 해석결과와 비교하였다. 본 연구에서 사용한 소형 풍력발전기 모델은 본 연구실에서 직접 설계 및 제작한 것으로 4개의 블레이드를 가지는 450 W급 모델이다. 수직축 풍력발전기에 대한 가속 성능시험은 차량장착시험 시스템(vehicle mounted testing system)을 이용하여 수행한 사례가 있다(2) 압출금형을 통해 만들어진 4개의 알루미늄 블레이드를 이용해 풍속 3 m/s에서 출력을 발생한다. 그리고 50 m/s의 풍속까지 견딜 수 있도록 설계되었으며, 외부 컨트롤러를 통해 정격출력 이상의 전력이 발생시, 전력을 가감(regulation)시키고 전기적으로 부하를 발생시켜(electronic torque control) 전기식 브레이크 개념으로 블레이드의 회전을 통제한다. 출력전압은 직류 12 V로 나와 축전지(battery bank)를 충전하도록 하였다. 풍력발전기의 제원을 간단히 설명하자면, 블레이드 길이 1.4 m, 로터직경이 1.4 m, 무게 40.2 kg, 컷인풍속(cut-in speed) 3 m/s, 정격풍속(regulated speed) 12 m/s이며 400 W급 전기발전기를 사용하였다. 그래프를 보면 정격풍속인 12 m/s에서 평균적으로 450 W가 도출하는 것을 볼 수 있다.

본 논문에서는 탄성 타워효과를 고려하였고, 개방형 풍동의 풍속을 변화시켜 다양한 풍하중으로 가진 조건을 부가하였다. 진동해석은 유한요소법 기반의 다물체 동역학 기법을 적용하였으며, 캠벨차트(Campbell chart)의 이론적인 공진특성과 공기역학 적인 가진 특성을 고려한 진동응답 특성을 파악해 보고자 한다.

2. 해석 및 실험기법

2.1 FEM 기법

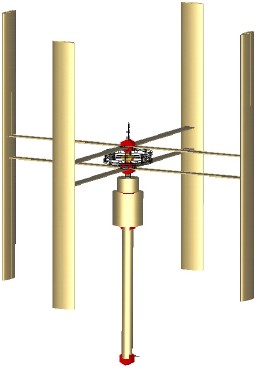
FEM 기법으로 상용구조해석프로그램을 활용하여 진동해석(vibration analysis)을 수행하였다. Fig. 1 (a)은 3D CAD 프로그램으로 모델링한 450 W급 소형 수직축 풍력발전기 모습으로 블레이드 직경 1.4 m, 블레이드 길이가 1.4 m 의 구조물이다. Fig. 1 (b)는 상용구조해석프로그램에서 진동해석하기 위해 풍력발전기를 beam으로 모델링(modeling)한 모습이고, Fig. 1 (c)는 mesh 모델이다.

본 모델의 경계조건은 발전기와 상하단 암 구조물, 발전기와 타워 사이와 같이 볼트로 체결되는 부분은 강체와 강체를 연결하는 조건인 고정(fixed) 조건을 부여하였다. 타워 하부 플랜지 부분에는 지상풍동베이스에 체결되어 있는데, 지상풍동베이스의 질량이 상당히 무거우므로 지면과 같다고 가정하여 6-자유도계를 구속시키는 clamp 조건을 부여하였다. 재료 물성치로 암 구조물, 타워, 발전기는 스테인레스 스틸(stainless steel)재질이므로 탄성계수(E, Young’s modulus)는 210 GPa, 푸아송비(poisson’s ratio)는 0.3, 그리고 질량밀도는 7,800 kg/m³ 를 입력하였다. 블레이드는 알루미늄을 사용하여 탄성계수는 70 GPa, 푸아송비는 0.3, 그리고 질량밀도는 2,750 kg/m³ 을 입력하였다. 발전기-타워 연결용 플랜지 구조물은 엔지니어링 플라스틱 재질을 사용하여 탄성계수가 101 GPa, 푸아송비 0.3, 질량밀도를 1,070 kg/m³ 를 입력하였다.

하중조건은 Table 1에 나오는 정보를 활용하여 풍력발전기 부품 별로 질량을 부가하였고, 중력효과를 고려하기 위해 구조물 전체에 9.81 m/s² 의 중력가속도를 부가하였다. 회전효과는 회전속도(rotation speed)로 풍력발전기 구조물에 부가하여 진동해석을 수행하였다. 50 rpm 단위로 0∼500rpm, 총 11번 반복 수행하여 캠벨차트를 도식하였다.

Fig. 1

450 W VAWT model(a) CATIA model

(b) FEM model

(c) FEM mesh model

2.2 가진실험기법

가진 응답 실험은 Fig. 2에서 제시하는 바와 같이 풍력발전기 타워의 가속도를 모니터링(monitoring) 할 수 있는 랩뷰시스템(Lab-VIEW system)과 스트레인 게이지(strain gage)를 이용하여 변형률(strain)을 모니터할 수 있는 P3 스트레인 인디케이터(P3 strain indicator)로 구성되어 있다. 랩뷰는 직관적인 그래픽 아이콘 및 컨트롤 시스템을 사용하는 그래픽 프로그래밍 환경기반으로, 계측 및 자동화를 위한 전문프로그램이다. P3 스트레인 인디케이터는 변형률을 측정하는 데 특화된 계측 장비로, 쿼터브릿지(quarter bridge)부터 풀브릿지(full bridge)방식까지 지원한다. 이 장비들을 이용하여 가속도 및 변형률을 측정하는 기법을 구축하였으며, 지상 풍동 베이스에 타워를 체결, 고정시켜 송풍기 회전수를 조절하여 풍력발전기의 RPM 변화에 따른 가속도와 변위응답을 측정하였다.

Table 1

450 W class vertical-axis wind turbine mass information

Figure 3 (a)는 수직축 풍력발전기를 타워에 체결시켜 지상 풍동 베이스에 설치한 모습이다. 본 연구실은 직경 50.1mm 인 타워를 사용하였는데, 이는 타워의 가진 응답 결과를 가시화시키기 위해서이다. Fig. 3 (b)를 보면 수직축 풍력발전기 바로 아래에 있는 엔지니어링 플라스틱 구조물에 RPM 측정기를 부착하여 풍력발전기의 회전수를 측정하였고, 타워 상단 플랜지 부분에 가속도계를 부착하여 회전수에 따른 가속도를 측정할 수 있도록 구축하였으며, 타워 하단 뿌리(root)부분에 하프 브릿지(half-bridge)방식으로 스트레인 게이지를 부착하여 회전수에 따른 변형률을 측정할 수 있도록 구축하였다. 가속도와 변형률은 송풍기에서 불어오는 바람의 방향을 x축으로 정하여 x축 방향과 그에 수직한 y축 방향, 두 개의 신호(signal)를 측정하였다. 풍력발전기 뒤에 보이는 송풍기에서 나오는 풍속으로 RPM 을 증감시키는 방법을 활용하여 20 rpm 씩 증가시키면서 가속도(g)를 측정하였고, 50 rpm 씩 증가시키면서 변형률(ε)을 측정하였다. 가속도의 경우 가속도의 평균값을 나타내는 RMS value 값을 측정하였다.

Fig. 2.

Excitation-response experiment equipment

Fig. 3.

450 W class VAWT on the wind tunnel ground base(a) VAWT installation on the wind tunnel ground base

(b) Attached position of the measuring equipment

3. 결과 및 검토

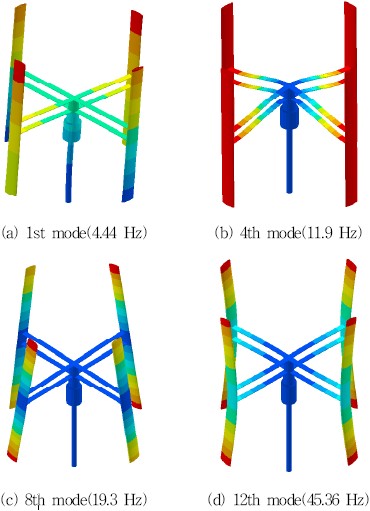
본 연구에서는 4-블레이드 소형 수직축 풍력발전기의 RPM 에 따른 가진 특성 분석에 대해 수행하였다. 고유진동모드 차수가 올라갈수록 진동수는 계단식 증가를 보인다. 이 풍력발전기는 1차(4.44 Hz), 2차(4.65 Hz) 고유진동수가 서로 유사하다. 이와 같이 나머지 4차(11.95 Hz), 5차(11.97 Hz), 6차(12.22 Hz), 7차(12.30 Hz) 고유진동수와 8차(19.35 Hz), 9차(19.39 Hz), 10차(19.61 Hz) 고유진동수가 서로 유사하다. 그리고 구조물의 고유진동수가 유사한 경우는 그 모드형상 또한 유사하다. Fig. 4는 고유진동수가 증가함에 따라 각 모드형상을 대표하는 고유모드들을 나타내고 있다. Fig. 4 (a)는 타워의 굽힘 모드, Fig. 4 (b)는 암 구조물의 굽힘 모드, Fig. 4 (c)는 블레이드와 암 구조물 사이 비틀림 모드, Fig. 4 (d)는 원심력에 의한 블레이드 굽힘 모드를 보여주고 있다. Fig. 4에서 대표모드형상과 유사한 모드는 제외하였다.

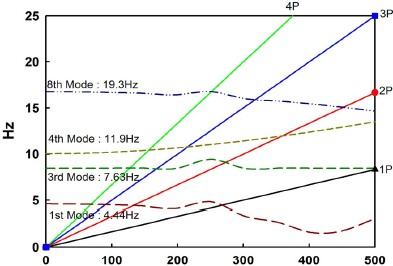
이를 토대로 Fig. 5와 같이 회전효과에 따른 전체 구조물의 campbell chart를 도출하였으며, 풍력발전기가 1차 고유진동모드와 1P 가 교차하는 지점인 268 rpm 에서 가장 큰 1차 공진이 발생할 수 있음을 확인하였다. 또한 이를 통하여 공진 회피방법으로 268 rpm 부근에서 제어기를 설치하여 지속적인 작동이 되지 않도록 약간의 조치가 필요함을 확인하였다.(3)

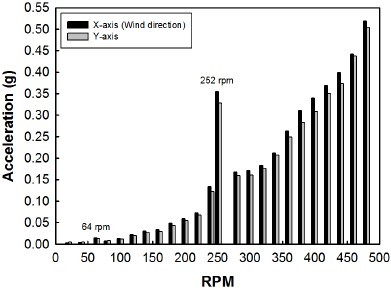
Figure 6은 가속도계를 이용하여 풍력발전기 회전수에 대해 가속도 변화를 나타낸 그래프이다. 64 rpm 과 252 rpm 에서 주변보다 심한 가속도가 측정되었다. 그리고 300 rpm 에서부터 가속도가 선형적으로 증가하는데, 풍력발전기의 편심하중에 의한 것임을 알 수 있다. 인력으로 제작한 풍력발전기는 정확한 좌우대칭으로 제작하기에 한계가 존재하기 때문에 고 RPM 에서 상당히 큰 편심하중이 발생하는 것은 불가피하다. 또한 모든 RPM 에서 x축의 가속도가 y축의 가속도보다 큰 값을 가지는 것을 볼 수 있는데, x축이 바람 방향이기 때문이다. 고 풍속으로 갈수록 풍하중은 증가하고, y축보다 x축의 가속도가 조금 크게 작용함을 알 수 있다.

Fig. 4.

Natural vibration mode shape

Fig. 5.

Campbell chart according to the rotational speed

Fig. 6.

Induced acceleration level vs. rpm.

Fig. 7.

Induced dynamic strain vs. rpm.

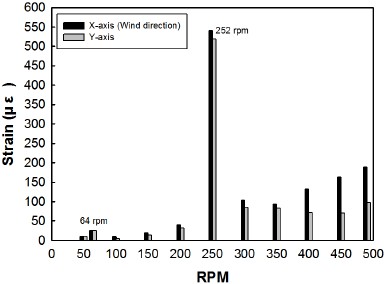
Figure 7의 실험결과를 보면 252 rpm 에서 540 με 정도로 상당히 큰 동적 변형률이 발생함을 볼 수 있다. 64 rpm 의 경우 주변 구간보다 높은 25.5 με 의 동적 변형률 수준을 보이지만, 252 rpm 에서의 공진조건에 비하면 무시 가능한 수준임을 알 수 있다. 그리고 그래프를 보면 64 rpm 에서의 동적 변형률은 300 rpm 에서부터의 동적 변형률 수준보다 2배 이상 낮은 것으로 보인다. 그러므로 저 RPM 에서의 공진 조건보다 고 RPM 에서 편심하중에 의한 진동현상이 더 위험함을 알 수 있다. 또한 Fig. 7을 보면 350 rpm 부터 x축 변형률이 선형적으로 증가하는 것을 볼 수 있다. 이는 Fig. 6 그래프의 고 풍속 영역에서 나타나는 결과와 같은 현상으로 편심에 의한 불평형으로 볼 수 있다. 풍속이 높아지면서 타워의 x축으로 동적 풍하중이 증가하고, x축은 y축보다 큰 변형률을 가지게 된다

Figure 5와 Figs. 6∼7을 비교해보면 Fig. 5에서 1차 고유진동모드와 4/rev 가 교차하는 지점인 64 rpm 과 Fig. 6에서 공진에 의한 가속도가 증가하는 지점인 64 rpm 이 정확히 일치하는 것을 볼 수 있으므로, FEM 해석결과가 정확하다는 것을 입증할 수 있다. 하지만 Fig. 5에서 1차 고유진동모드와 1/rev 가 교차하는 지점인 268 rpm 과 Fig. 6에서 공진에 의한 가속도가 측정되는 지점인 252 rpm 은 약 16 rpm 의 차이가 남을 알 수 있다. 이 오차의 이유는 첫 번째로 실제모델에서의 암 구조물은 테이퍼가 주어진 구조물인데 반해, FEM 모델에서 beam모델링은 실제와 일치하게 모델링되지 못하기 때문에 이런 오차가 발생했다. 두 번째로 FEM 모델에서 모델링한 타워의 재질 특성과 실제 타워의 재질 특성이 정확하게 일치하지 않아 가상 타워가 실제 타워보다 유연하게 모델링 되었다고 볼 수 있다. 마지막으로 해석에서는 타워의 감쇠(damping)작용을 고려하지 않았지만, 실험에서는 타워의 감쇠작용이 고려되어 측정값이 도출되었다. 요컨대, 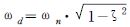(ω_d : 실험에서의 고유진동수, ω_n : 이론에서의 고유진동수)식에 의해 실험결과가 해석결과보다 낮은 RPM 에서 공진가능성이 발생했다고 판단된다.

풍력 시스템 및 타워설계 시 최우선적으로 1P 와 1차 고유진동모드가 교차하는 공진회전 조건은 절대적으로 회피할 필요성이 있다. 그리고 본 논문을 통해 실제 10∼20 m 정도의 전용타워 설계가 이루어진 경우에는 이에 대한 등가 강성수준을 반영하여 실제 타워 설치조건과 유사하게 가속 평가하는 것이 가능함을 중요하게 파악할 수 있다.

4. 결 론

본 연구에서는 타워의 강성효과를 고려하여 4개의 블레이드를 가지는 소형 수직축 풍력발전기 모델에 대해 운전진동실험과 전산해석을 수행하였다. 실험 및 해석을 통하여 전형적으로 회전 공진안정성을 확인하는 캠벨차트에서 1P 과 1차모드의 교차점이 가장 지배적인 공진 현상을 유발함을 실험을 통해 입증하였다. 이론 해석결과에서는 캠벨차트에 전형적으로 다양한 공진 가능성이 나타나게 된다. 하지만, 실제실험을 수행해본 결과 1차 주요 공진조건 이외에는 바람 방향으로의 풍속 및 회전속도 증가에 따른 동적 풍하중 증가가 시스템 진동 불안정성의 주요 원인으로 작용하게 됨을 중요하게 보였다. 본 연구 결과는 복잡하고 난해한 수직축 풍력발전기 및 타워의 최적 구조설계 과정에 매우 유용하게 활용될 수 있을 것으로 판단된다.

Acknowledgments

본 논문은 2011년도 지식경제부의 재원으로 한국 에너지기술평가원(KETEP)의 지원을 받아 수행한 연구내용의 일부이며, 지원에 감사를 표하는 바입니다 (No. 20114010203070).

References

• 김동현, 박강균, 이종욱, 최현철, 김동만, 김요한, “800W급 양력형 수죽축 풍력발전기 개발”, 한국풍력에너지학회 추계 학술대회, (2009).
• 이종욱, 김동현, 박강균, 최현철, 김대룡, “차량장착시험시스템(VMTS)을 이용한 소형 풍력발전기시스템의 성능평가”, 한국풍공학회지, (2010), 14(3), p207-213.
• 김동현, 류경중, 김요한, 김성복, 김광원, 남효우, 이명구, “타워를 포함한 6kW급 수직축 풍력발전기 구조진동해석”, 한국소음진동공학회 춘계학술대회, (2011), P304, p663-670.