[ Article ]

The KSFM Journal of Fluid Machinery - Vol. 16, No. 3, pp.32-38

ISSN: 2287-9706 (Print)

Print publication date Apr 2013

Received 05 Mar 2013 Revised 01 May 2013 Accepted 07 May 2013

DOI: https://doi.org/10.5293/kfma.2013.16.3.032

Rotordynamic Analysis and Experimental Investigation of the Turbine-Generator System Connected with Magnetic Coupling

KimByung Ok^*^{, †} ; ParkMoo Ryong^** ; ChoiBum Seok^**

*KIMM, Department of system dynamics **KIMM, Department of extreme energy systems

마그네틱 커플링으로 연결된 터빈-발전기 시스템의 로터다이나믹 해석 및 실험적 고찰

Correspondence to: † kbo2612@kimm.re.kr

This paper deals with the study on the rotordynamic and experimental analysis of turbine-generator system connected with a magnetic coupling. Although magnetic coupling has been used to torque transmission of chemical processing pump rotating at under 3,600rpm, magnetic coupling in this study is applied to high-speed turbine-generator system using a working fluid that is refrigerant such as ammonia or R-124a. Results of rotordynamic design analysis are as follows. The first, shaft diameter nearest to outer hub of magnetic coupling has a big effect on the 1st critical speed of generator rotor. The second, if the 1^st critical speeds of turbine rotor and generator rotor have enough to separation margin in comparison to rated speed, the 1^st critical speed of turbine-magnetic coupling-generator rotor train has enough to separation margin regardless of connection stiffness of magnetic coupling. The analytical FE model is guaranteed by impact test on the prototype and condition monitoring such as measurements of vibration and bearing temperature is also performed.

Keywords:

Magnetic coupling, Temperature differential power system, Critical speed, Connection stiffness, Operating fluid, 마그네틱 커플링, 온도차 발전시스템, 위험속도, 연결강성, 작동유체

1. 서 론

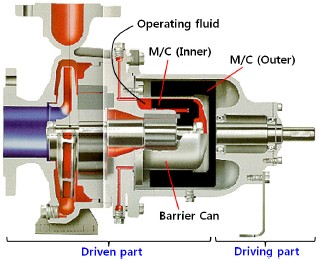
마그네틱 커플링(magnetic coupling, M/C)(1)은 자기력을 이용하여 동력을 전달하는 대표적인 비접촉식 커플링이다. 마그네틱 커플링은 접촉식 커플링에 비해 진동절연 효과를 기대할 수 있으며, 특히 인체와 환경에 유해한 작동유체로 운전되는 회전기계에 토오크 전달용으로 많이 활용되고 있다(2). Fig. 1은 펌프 구동에 적용된 동축형(axial type) 마그네틱 커플링의 사용예를 제시하였다(3). 그림에서 보는 바와 같이 마그네틱 커플링 내·외륜 사이에 격벽(barrier can)이 있어 피동부측 작동유체의 기밀이 유지되면서 토오크가 전달되고, 동시에 과도한 토오크가 전달될 경우, 슬립(slip)이 발생하여 기계적인 손상을 방지할 수 있다. 본 연구에서는 이러한 마그네틱 커플링의 장점을 이용하여 터빈-발전기의 연결장치로 활용한 사례에 대해 논의하고자 한다.

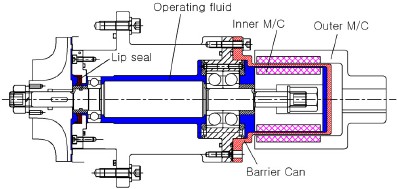
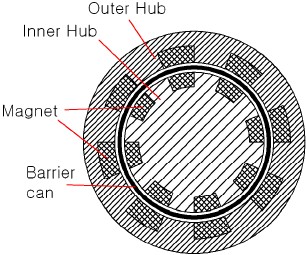
설계된 터빈은 저온 온도차 발전시스템 개발의 일환으로 개발되었으며, 온도차 발전에 사용되는 작동유체는 인체와 환경에 유해한 냉매를 사용하기 때문에 완전 밀봉이 요구된다. 밀봉을 위하여 접촉 시일(contact seal)과 오링(O-ring)을 사용하지만, 장기간 사용 시 시일 마모와 베어링 측으로 누설이 진행될 수 있다. 따라서, Fig. 2에서와 같이 터빈 축에 마그네틱 커플링의 내륜을 장착하고 내부 유체를 격벽으로 완전히 밀봉시키는 방법을 채택하였다. Fig. 3에 적용된 동축형 마그네틱 커플링을 제시하였다. 극(pole)수는 8개, 공칭(nominal) 전달 토오크는 16N·m, 자석 재질은 Sm2Co17이다.

Fig. 1

Example of pump system driven by M/C

Fig. 2

Proposed turbine system driven by M/C

Fig. 3

Cross section of axial type M/C

최근까지 마그네틱 커플링은 대부분 펌프구동에만 적용되어 왔다. 펌프의 경우 최대 회전속도가 3,600rpm미만으로 구동되기 때문에 로터다이나믹적 문제가 거의 발생되지 않았으나, 개발 대상 시스템의 경우, 15,000rpm으로 터빈을 구동시키기 때문에 터빈-마그네틱 커플링-발전기 시스템의 회전 신뢰성이 매우 중요하다. 본 연구에서는 마그네틱 커플링을 포함한 로터 트레인의 위험속도 분석, 불균형 응답해석 등 상세한 로터다이나믹 해석을 수행하여 회전 신뢰성을 검토하였다. 또한 시제품을 제작하여 정격부하에서 진동특성 및 베어링 온도 측정 등 상용화를 위한 전반적인 사항을 검토하였다.

Fig. 4

Schematic of turbine-M/C-generator rotor train

2. 해석 모델링

2.1. 로터 모델링

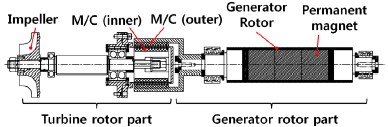
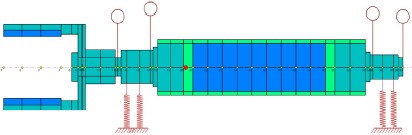
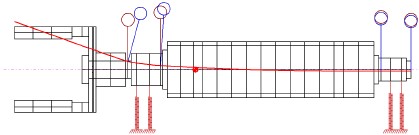
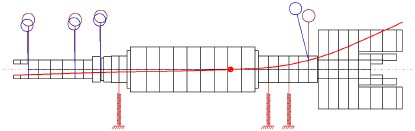
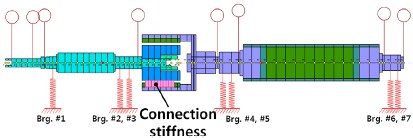
해석 대상 터빈-마그네틱 커플링-발전기 로터의 개략도를 Fig. 4에 제시하였다. 발전기 용량은 20kW이며, 정격회전속도는 15,000rpm이다. 터빈부는 터빈 임펠러, 터빈 축, 마그네틱 커플링 내륜으로 구성되어 있으며, 발전기부는 마그네틱 커플링 외륜, 발전기 회전자로 구성되어 있다.

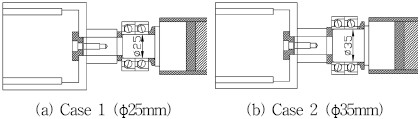
해석 대상 모델에서는 기존 로터-베어링 시스템과는 달리 마그네틱 커플링으로 연결되어 있기 때문에 이 부분의 해석모델이 중요하다. 특히, 발전기 측은 끝단에 상대적으로 무거운 마그네틱 커플링 외륜이 장착되기 때문에 베어링이 장착되는 위치에서의 축직경 크기가 로터다이나믹 특성에 큰영향을 미칠 것으로 예상된다. 축직경이 작을 경우 고속용베어링 선정에 유리하고, 축직경이 커지면 동적 특성은 좋아질 수 있으나 고속용 베어링 선정에는 다소 불리할 수 있다. Fig. 5에 두 가지 축직경을 제시하였으며, 각각에 대한 로터다이나믹 특성을 3.1절에서 기술하였다. Fig. 6와 Fig. 7에 발전기와 터빈의 로터다이나믹 FE(finite element) 해석모델을 제시하였다.

Fig. 5

Design case of journal shaft diameter

Fig. 6

FE model of generator rotor (Case 2)

Fig. 7

FE model of turbine rotor

3. 로터다이나믹 해석

로터다이나믹 FE 해석모델의 수치해석은 개개의 빔 요소, 등가질량⋅관성요소, 베어링 요소, 그리고 불균형 가진요소등을 조합하여 얻어진 방정식으로부터 위험속도 및 모드해석, Campbell 선도, 불균형 응답해석 등을 수행하는 것이다.

3.1. 발전기 및 터빈 로터의 위험속도 해석

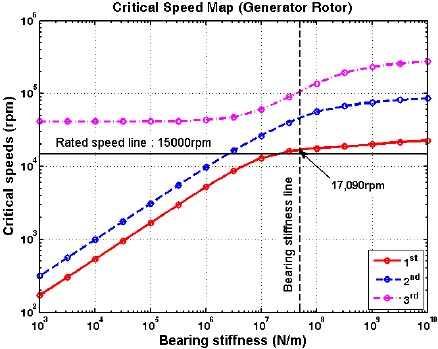
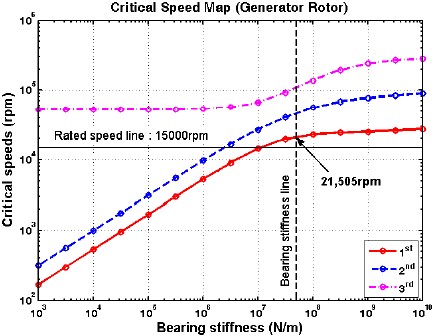
시스템의 감쇠와 연성효과를 고려하지 않은 상태에서 베어링의 지지위치와 강성에 따른 위험속도를 평가하는 방법으로 위험속도 선도가 사용된다. 발전기 로터(case 1과 case 2)와 터빈로터 각각에 대한 1, 2, 3차의 정선회(1X-forward whirl) 위험속도를 나타내는 위험속도 선도를 Fig. 8, 9 및 10에 각각 제시하였다. 불균형 가진력처럼 회전속도와 동일한 가진력은 정선회 위험속도와 공진을 일으키기 때문에 정선회 위험속도를 우선적으로 파악하여야 한다. 볼베어링 강성계산식(4)을 적용하여 산출된 강성은 대략 5×107 N/m이며, case 1 발전기의 경우 베어링 강성에 대응되는 1차 위험속도(1X)는 17,090rpm으로 계산되었다. 발전기 정격속도의 과속도(over-speed) 기준 10%(16,500rpm)를 고려할 때, 분리여유가 거의 없기 때문에 축직경 φ25mm는 적절치 않을 것으로 판단된다.

Fig. 8

Critical speed map of generator rotor (Case 1)

Fig. 9

Critical speed map of generator rotor (Case 2)

Fig. 10

Critical speed map of turbine rotor

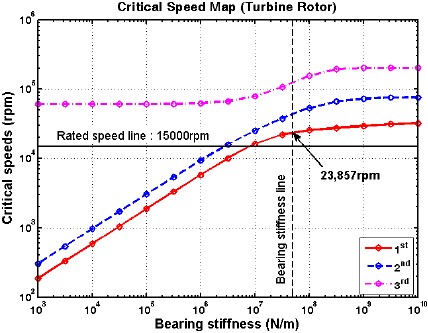
축직경이 φ35mm인 case 2의 경우 1차 위험속도(1X)는 21,505rpm으로 계산되었으며, 과속도를 고려하더라도 30%의 분리여유를 가지기 때문에 case 2로 채택하여 설계⋅제작을 수행하기로 하였다. 한편 터빈로터의 1차 위험속도(1X)는 23,857rpm으로 과속도와의 분리여유가 45% 이므로 1X에 의한 공진은 없을 것으로 판단된다.

위험속도에 대응되는 모드형상(mode shape)은 관련된 위험속도 근방에서 로터의 상대적인 동적거동 예측을 가능하게 하며, 불균형 응답 예측시 불균형 위치를 규정할 때 유용하게 사용된다. Fig. 11과 Fig. 12는 발전기 로터와 터빈로터의 1차 위험속도에 대응되는 모드형상을 각각 나타내었다. 그림에서 보는 바와 같이 마그네틱 커플링이 장착된 부분에서 상대적으로 큰 진폭을 가짐을 알 수 있다.

Fig. 11

1st mode shape of generator rotor (Case 2)

Fig. 12

1st mode shape of turbine rotor

해석 모델의 검증을 위하여 실제 제작된 발전기와 터빈 로터를 대상으로 임팩트 테스트를 수행하였다(Fig. 13과 14 참조). 가속도 센서를 마그네틱 커플링 외륜과 내륜 끝단에 부착하였고, 임팩트 햄머를 가속도 센서 근방에 타격하였다. 정지된 상태에서 1차 고유진동수 비교 결과를 Table 1에 제시하였으며, 그 결과 1% 미만의 차이를 가져 FE 해석모델에 대한 타당성을 확보하였다.

Fig. 13

Impact testing of generator rotor

Fig. 14

Impact testing of turbine rotor

Table 1

Comparison results of 1st natural frequency

3.2. 결합된 로터의 위험속도 해석

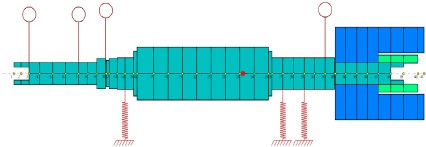
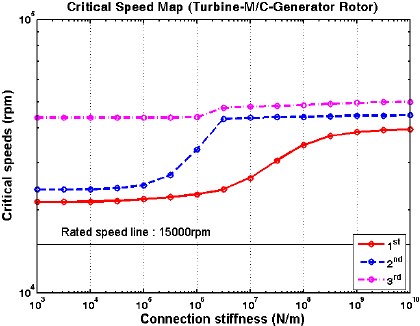
앞서 언급한 내용들은 발전기와 터빈로터에 대한 개별적인 위험속도 해석을 수행하였다. 그러나 발전기와 터빈은 마그네틱 커플링으로 연결되어 있어, 전체 트레인의 위험속도해석이 요구된다. Fig. 15에 전체 트레인에 대한 FE 해석모델을 제시하였다. 마그네틱 커플링의 자기력에 의한 연결강성(connection stiffness)은 마그네틱 커플링의 외륜과 내륜을 스프링 강성으로 대체하여 모델링하였다. 연결강성에 의한 위험속도 변화를 고찰하기 위하여 볼베어링의 강성은 5×10⁷ N/m으로 고정시킨 후, 연결강성만 변화시켜 위험속도 해석을 수행하였으며, 그 결과를 Fig. 16에 제시하였다.

그림에서 보는 바와 같이 마그네틱 커플링의 연결강성에 상관없이 정격속도까지 위험속도가 존재하지 않음을 알 수 있다. 이 결과는 발전기와 터빈 로터가 마그네틱 커플링으로 연결되어 있더라도 각각 분리해서 위험속도와의 분리여유검토를 가능하게 하는 중요한 정보이다. 연결강성을 고려한 상태에서 1차 위험속도는 22,878rpm이며, 대응되는 모드형상을 Fig. 17에 제시하였다. 이때, 적용된 마그네틱 커플링 연결강성은 일반적인 값인 1×10⁶ N/m(5)를 사용하였다. 연결된 모드형상은 터빈과 발전기의 1차 위험속도에 대응되는 모드형상을 중첩시킨 것과 동일함을 알 수 있다.

Fig. 15

FE model of turbine-M/C-generator rotors

Fig. 16

Critical speed map of turbine-M/C-generator rotors

Fig. 17

1st mode shape of turbine-M/C-generator rotors

Fig. 18

Campbell diagram of turbine-M/C-generator rotors

3.3. 켐벨선도(Campbell diagram) 해석

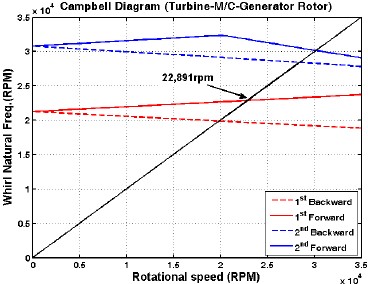
시스템의 감쇠와 연성효과를 고려하여 회전속도의 함수로 선회고유진동수(whirl natural frequency)를 Fig. 18에 나타내었다. 불균형 가진력처럼 회전속도와 동일한 가진력은 정선회 위험속도와 공진을 일으키기 때문에 1X-동기회전수선과 교차되는 곳이 정선회 위험속도이다. 본 시스템의 경우 볼베어링에서의 감쇠를 5%로 적용하였으며, 이때 1차 정선회 위험속도는 각각 22,891rpm으로 정격속도 및 과속도와 의 분리여유가 충분함을 알 수 있다.

3.4. 불균형 응답해석

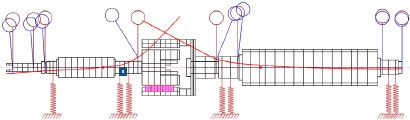
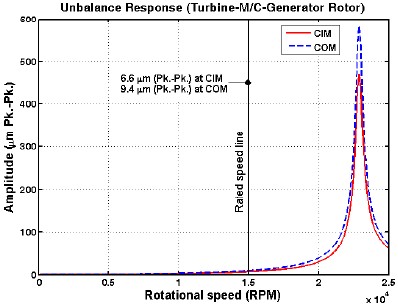
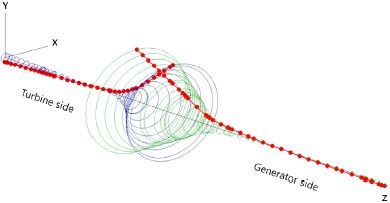
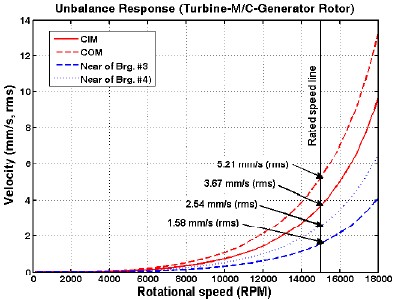
불균형 작용 시 터빈-마그네틱 커플링-발전기 시스템의 진동응답을 예측하기 위하여 ISO G2.5 등급(터빈측 : 4.69g•mm, 발전기측 : 12.38g•mm)에 해당하는 불균형을 Fig. 11과 12의 모드형상을 참고하여 마그네틱 커플링 내⋅외륜에 각각 부가하였다. 회전속도에 따른 변위응답을 Fig. 19에 제시하였다. 앞서 언급한 바와 같이 22,900rpm에서 위험속도에 의한 공진으로 진폭이 매우 커짐을 알 수 있다. 그러나 정격속도에서는 터빈측 마그네틱 커플링 내륜중심(CIM)과 발전기측 마그네틱 외륜중심(COM)에서의 진동변위는 10㎛(Pk.-Pk.)미만으로 예측되었다. Fig. 20은 정격속도에서 전체 시스템의 진동패턴을 나타낸 그림으로서, 대부분의 진동은 마그네틱 커플링에서 발생되고 있음을 보여준다. 볼베어링으로 지지되는 회전기계의 경우, API(6)에서는 진동레벨 기준을 속도로 규정하고 있기 때문에 진동응답을 속도로 나타낼 필요가 있다. API 기준에 근거한 진동속도 제한치는 베어링 하우징 근방에서 측정한 진동레벨이 3mm/s(rms)로 제한하고 있다. Fig. 21에 각 중요한 지점에서의 불균형 진동응답을 속도레벨로 제시하였다. 정격속도에서 마그네틱 커플링에서의 진동속도레벨은 API 기준을 초과하지만, 베어링근방에서의 속도레벨은 기준을 만족하고 있음을 알 수 있다.

Fig. 19

Unbalance response with rpm (Center of inner M/C(MIC), Center of outer M/C(COM)

Fig. 20

Unbalance respone pattern at rated speed

Fig. 21

Unbalance respone (velocity) pattern at rated speed

4. 발전기 및 터빈 로터의 회전테스트

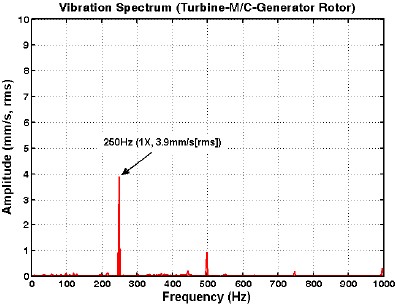
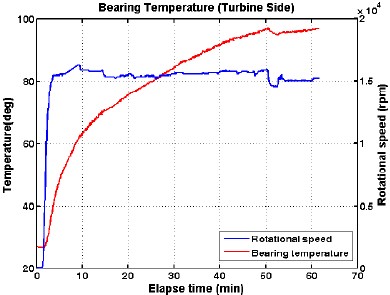
앞서 제시한 설계해석을 토대로 터빈과 발전기를 설계 및 제작하여 회전테스트를 수행하였다. Fig. 22에 시험장면을 제시하였으며, 터빈의 구동은 압축공기를 사용하였다. 마그네틱 커플링 외륜에 회전속도를 감지하기 위하여 반사테이프를 부착하였고, 진동측정을 위하여 마그네틱 커플링 외륜과 가장 가까운 발전기 하우징에 속도센서를 부착하였다. 부하조건에 따른 진동레벨은 거의 일정하였으며, 최대 부하인 20kW일 때, 정격속도에서의 진동 스펙트럼을 Fig. 23에 제시하였다. 정격속도에서 1X 성분의 진동레벨은 3.9mm/s (rms)로 해석 예측값(2.5mm/s, rms) 보다 다소 높게 측정되었다. 해석과 실험값의 차이는 테스트 베드의 지지 유연성 (flexibility)에 의한 영향으로 판단된다. Fig. 15에 표시한 Brg. #2(angular contact bearing)에서의 온도변화를 Fig. 24에 제시하였다. 베어링의 외륜을 측정하였으며, 정격속도 15,000rpm에서 약 1시간 동안 온도 측정한 결과, 포화온도가 100℃ 미만으로 적용조건(7)에서 양호함을 알 수 있다.

Fig. 22

Rotating test of turbine-M/C-generator rotor

Fig. 23

Vibration spectrum at the generator housing

Fig. 24

Monitoring of bearing temperature

5. 결 론

본 연구에서는 마그네틱 커플링으로 연결된 터빈-발전기 시스템의 회전 신뢰성을 확보하기 위한 로터다이나믹 설계해석과 설계 반영된 시제품에 대한 실험적 해석을 수행하였다. 마그네틱 커플링은 인체와 환경에 유해한 작동유체로 운전되는 펌프 동력전달용으로 주로 사용되어 왔으나, 저온 온도차 발전시스템 개발의 일환으로 냉매를 작동유체로 사용하는 고속 터빈-발전기 시스템에 적용하였다. 로터다이나믹 설계해석에서 가장 핵심적인 사항은 다음과 같다. 첫째, 마그네틱 커플링 외륜과 가까운 쪽의 발전기 축직경은 로터의 1차 위험속도에 매우 큰 영향을 끼치며, 둘째, 터빈로터와 발전기 로터 각각의 1차 위험속도가 정격속도와의 분리여유가 충분하면, 마그네틱 커플링의 연결강성에 상관없이 터빈-마그네틱 커플링-발전기 로터 트레인의 1차 위험속도 또한 정격속도와의 분리여유가 충분하다. 해석모델의 검증을 위하여 시제품에 대한 임팩트 시험을 수행하여 해석모델의 신뢰성을 확보하였으며, 시제품에 대한 부하시험을 통하여 진동과 베어링 온도측정등 회전 건전성 판단 위한 상태 모니터링도 수행하였다.

Acknowledgments

본 연구는 국토해양부에서 지원하는 ‘해양심층수의 에너지 이용 기술 개발’ 결과임을 밝히며, 연구비 지원에 감사드립니다.

References

김성걸, 이성진, 이장무, “마그네틱 커플링을 장착한 축계의 동적해석(I)”, 한국정밀공학회지, (1994), 11(4), p99-105.
김성걸, 이장무, “마그네틱 커플링을 장착한 축계의 동적해석(II)”, 한국정밀공학회지, (1995), 12(7), p107-113.
박헌, “마그네틱 커플링을 장착한 회전축계의 진동해석에 관한 연구”, 서울대학교 석사학위논문, (1992).
Harris, T. A, “Rolling Bearing Analysis”, JohnWiley & Sons, (2001).
Wu, W., Lovatt, H. C., Dunlop, J. B., “Analysis and design optimization magnetic couplings using 3D finite element modeling”, Magnetics Conference, Digests of INTERMAG ’97, (1997.).
API STANDARD 684, “Rotordynamics Tutorials: Lateral Critical Speeds, Unbalance Response, Stability, Train Torsional, and Rotor Balancing”, (2005.).
Johannes, B., Paul, E., Ball and Roller Bearings-Theory, Design and Application, Wiley, New York, (1999).

Rotor	Impact Test (Hz)	FE Model (Hz)	Diff. (%)
Generator	330	333	0.9
Turbine	365	367	0.5