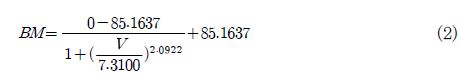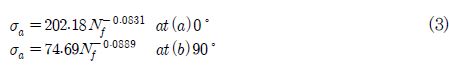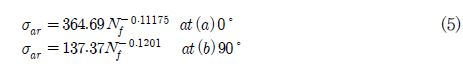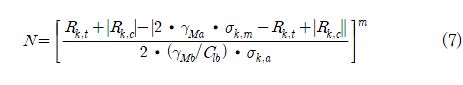Evaluation for Fatigue Resistance of Small Wind Turbine Composite Blade according to GL Guideline
This study aims to estimate the fatigue resistance of small wind composite blade using the fatigue life estimation formula in the GL guideline. For this, firstly, we estimated a turbine blade’s bending moment spectrum by using wind profile wind profile and BEMT. And fatigue tests were performed to obtain the S-N curve of composite materials used in blade. In addition, a finite element analysis was used to identify fatigue critical locations and fatigue stress spectrum. And the fatigue resistance of composite blade were evaluated using the rainflow cycle counting, and Goodman diagram and the fatigue life estimation formula in the GL guideline.
Keywords:
Composite blade, Fatigue resistance, GL guideline, Small wind turbine, 복합재 블레이드, 피로 저항성, GL 규격, 소형풍력발전기1. 서 론
운영 중 블레이드 작용하는 외력은 바람의 공력(Aerodynamic force)에 의한 굽힘 하중(Bending load), 난류(Turbulence) 및 돌풍(Gust) 등이 있으며 이로 인하여 피로하중(Fatigue load)을 받게 된다.(3) 피로하중에 대한 저항성(Fatigue resistance)을 극대화하기 위하여 블레이드는 섬유강화 고분자 복합재료(Fiber reinforced plastics)를 사용하여 설계 및 제작된다.(2) 또한, 풍력발전기 국제 규격인 IEC 61400 규격에서는 20년 이상의 설계수명(Design life)을 요구하고 있다. 따라서 풍력발전기 블레이드는 운영 중 작용하는 피로하중에 대한 저항성을 보유하여야하며(3) 특히 블레이드 제작 시 사용하는 복합재료는 기존의 금속재료와는 매우 상이한 피로 거동을 보이므로 이를 고려한 피로 수명 또는 피로 저항성 평가가 필요하다.(45)
복합재 블레이드에 대한 피로 수명 평가를 위한 연구는 다양하게 수행되고 있다. 공창덕 등(6)은 미국에서 측정된 피로하중 스펙트럼 및 Spera(7)의 굽힘 모멘트 관련 경험식을 적용하여 중형 복합재 블레이드의 피로 해석을 수행하였다. Ronold 등(8)은 블레이드의 피로저항성 평가를 위하여 플랩방향(Flapwise) 바람 유발 굽힘 모멘트(Wind-induced bending moment)에 대한Weibull 분포 및 손상 누적에 대한 Miner rule(9)을 기반으로 피로해석방법을 제시하였다. 상기의 연구들은 중대형 블레이드를 대상으로 우수한 해석결과를 제시하였으나 소형 풍력발전기 경우 풍황 특성이 매우 상이한 문제점 등으로 인하여 상기 연구 절차의 직접적인 적용은 곤란하다.
소형 복합재 블레이드의 피로수명 평가에 대한 연구의 경우, Wu 등(10)은 IEC 61400-2(11)에 정의된 단순 하중 계산식(Simplified load calculation)을 이용하여 재료의 부분 안전계수(Partial safety factors)에 따른 설계 수명을 계산하였다. Epaarachchi 등(12)은 호주 기상청(Australian Bureau of Meteorology)에서 측정한 단기 공탄성과 단기 및 장기 풍속 자료를 적용하여 블레이드의 피로하중 스펙트럼을 개발하였다. 이상의 연구들은 소형풍력발전기 블레이드를 대상으로 수행되었지만 중대형에 비하여 활발한 연구 경향을 보이지 않으며, 특히 IEC 및 GL 규격(13)의 표준화된 절차에 따른 연구는 거의 없는 실정이다.
본 연구에서는, 먼저 측정된 풍속 자료에 BEMT(Beam element momentum theory)를 적용하여 블레이드에 작용하는 굽힘 모멘트 스펙트럼(Bending moment spectrum)을 산출하였다. 또한, 유한요소해석(Finite element analysis)을 수행하여 피로취약지점(Fatigue critical location)을 확인하고 이를 토대로 피로응력 스펙트럼(Fatigue stress spectrum)을 획득하였다. 이러한 자료들에 Rainflow cycle counting 및 Goodman diagram을 적용하였다. 또한, 안전계수를 고려한 GL 규격의 수명 계산식 및 Miner’s rule을 이용하여 복합재 블레이드의 피로 저항성을 평가하였다.
2. 피로 저항성 평가 방법
본 연구에서는 소형풍력발전용 복합재 블레이드의 피로 저항성을 평가하고자 하며 Table 1은 이의 사양을 나타낸 것이다.
2.1. 공력 해석
본 연구의 대상인 블레이드의 공력 특성 및 하중을 평가하기 위하여 상용 프로그램인 PROPID(14)를 사용하였다. 이러한 과정을 통하여 산출된 각 풍속에 대한 하중을 BEMT를 이용하여 블레이드 구간(Section)별로 작용하는 굽힘 모멘트를 산출하였다. 이 때의 구간은 총 10개이며 각 0.13m의 폭을 가진다.
2.2. 실측 풍속
전북 군산시 비응도 비응공원에 풍속 계측기를 설치하여 2012년 2월 28일부터 4월 12일까지 0.2Hz의 속도로 풍속을 측정하여 데이터를 획득하였다. 사용된 풍속계는 WENIT사의 Davis Vantage Pro2이며, 지상으로부터 약 5m 지점에 설치하였다.
2.3. 피로 시험
블레이드의 재료에 대한 피로 특성 평가를 위하여 피로 시험을 수행하였다. 이는 응력비 R=0.1에서의 일정진폭 시험으로, 부하된 하중은 인장강도의 60%, 50%, 40% 및 35%의 4수준으로 수행되었다. 이 때, 주파수는 2Hz이고, 무한수명은 106으로 설정하였으며 사용된 시험장비는 Instron 8801 유압식 피로시험기이다.
블레이드의 재료는 DBL600E 삼축(Triaxial) 유리섬유강화 복합재료(Glass/epoxy composite material)로서 0˚ 및 ±45˚ 섬유가 모여 하나의 플라이(Ply)를 구성하는 스티칭(Stitching) 형태이다. 이러한 재료를 이용한 시험편은 피로 특성에 미치는 삼축[0˚/+45˚/-45˚]의 섬유 방향과 하중 방향의 영향을 평가하기 위하여 0˚ 방향의 섬유를 기준으로 0˚ 및 90˚ 방향으로 구분하여 가공하였다. 여기서 하중 방향은 실제 블레이드 제작 시 주로 사용되는 섬유 및 하중 방향을 고려하여 선택하였다. 또한, 진공성형 핸드 레이업(Vacuum assisted hand layup) 및 상온 경화 조건을 이용하여 제작되었으며 플라이 수는 5장으로서 제원은 20×200×3mm이다.
2.4. 유한요소해석
블레이드의 피로취약지점 확인 및 이에 따른 응력을 획득하기 위하여 상용 소프트웨어인 ABAQUS(15)를 이용하여 절점하중(Nodal force) 및 단위하중(Unit load) 해석을 수행하였다. 블레이드 형상은 Fig. 1과 같고 쉘 요소(Shell element)의 S4R 및 S3R을 사용하였으며, 요소(Element)의 개수는 19035개이고, 절점(Node)의 개수는 19074개이다. 하중은 2.1절에서 획득한 공력하중을 절점하중으로 변환한 조건과 블레이드 끝단에 1N을 부여한 조건을 적용하였다. 여기서 경계조건은 루트(Root)부분의 X, Y, Z 방향 및 Y, Z 회전방향의 자유도를 구속하였다.
2.5. 피로 저항성 평가
2.1 절의 과정을 통하여 도출된 풍속-굽힘 모멘트 관계식에 2.2절에서 측정한 풍속 데이터를 적용하여 굽힘 모멘트 스펙트럼을 산출하였다. 이에 2.4절에서 획득한 응력 데이터를 이용하여 굽힘 모멘트와의 관계식 및 피로응력 스펙트럼을 산출하였다. 이러한 피로응력 스펙트럼에 Rainflow cycle counting을 이용하여 응력범위(Stress range) 및 평균응력(Mean stress)으로 구분하는 Markov matrix로 나타내었다.
그러나 이는 임의의 평균응력을 가짐으로 Goodman diagram을 이용하여 0의 평균응력을 가지는 데이터로 변환하였으며, 또한 응력비 R=0.1로 수행한 피로 시험 데이터도 변환하였다. 이를 GL 규격의 응력 레벨에 대한 피로 수명 계산식에 적용하였으며, 이 때 S-N 곡선의 기울기를 나타내는 지수 m은 GL 규격에 정의된 값 및 실제 시험 값을 적용하였다. 이를 통하여 Miner’s rule에 적용한 두 값의 저항성을 평가 및 비교하였다.
3. 결과 및 고찰
3.1. 공력 해석
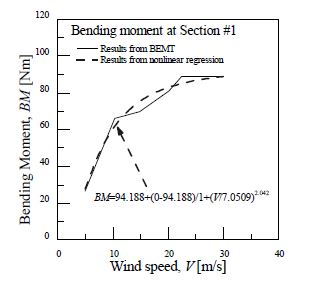
공력해석을 수행하여 획득한 하중을 BEMT를 이용하여 블레이드 각 구간별 풍속에 대한 굽힘 모멘트로 산출하였다. 이 중 최대 굽힘 모멘트를 가지는 구간 1에 대한 결과를 Table 2에 나타내었다. 이러한 풍속-굽힘 모멘트 곡선에 비선형 회귀 분석(Nonlinear regression analysis)을 적용하여 모멘트 스펙트럼을 획득할 수 있는 식 (1)을 산출하였으며, 이에 대한 결과는 Fig. 2에 나타내었다.
3.2. 실측 풍속
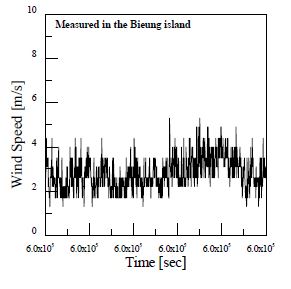
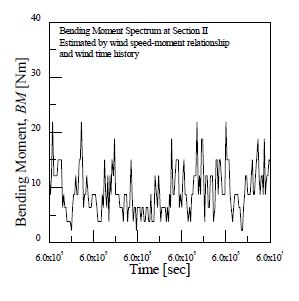
전북 군산시 비응도 비응공원에서 0.2Hz로 42일 동안 측정된 데이터의 총 개수는 약 620,000개이며 이의 일부분을 Fig. 3에 나타내었다. 2.3절에서 수행한 절점하중 해석을 통하여 발견한 피로취약지점에 대한 3.1절에서의 굽힘 모멘트 관계식은 식 (2)와 같다. 이러한 식에 풍속을 대입하여 굽힘 모멘트 스펙트럼을 획득하였다. 이에 대한 결과는 Fig. 4에서 볼 수 있으며, Fig. 3의 풍속과 동일한 시간에 대한 결과이다.
3.3. 피로 시험
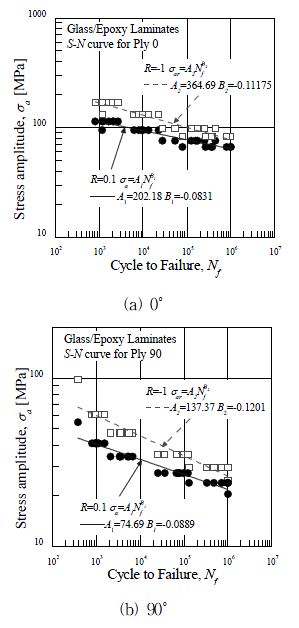
블레이드의 재료에 대한 피로 특성을 평가하기 위하여 0˚ 및 90˚ 시험편을 대상으로 응력비 R=0.1 및 4수준의 하중 조건에서의 피로시험을 수행하였다. 이러한 결과는 Fig. 5에 나타내었으며, Fig. 5 (a) 및 5 (b)는 하중 방향에 대하여 0˚ 및 90˚ 방향의 시험결과를 나타낸 것이다. 또한, 각 그래프에서의 원형 마크는 시험의 원결과를 나타낸 것이며, 이에 대한 결과를 Basquin’s equation에 의하여 평가하였고 이를 실선 및 식 (3)에 나타내었다.
여기서 σ a는 작용한 응력진폭, Nf는 피로 수명을 나타낸다.이러한 데이터를 피로 수명 평가에 적용하기 위해서는 식 (4)의 Goodman diagram(16)을 이용하여 응력비 R=-1로 변환시켰다. 이는 Fig. 5에 사각형 마크로 나타내었으며, Basquin’s equation에 의한 값은 점선 및 식 (5)에 나타내었다.
여기서 σ ar은 R=-1일 때의 피로응력, σ m은 평균응력, σ u는 인장강도이다.
3.4. 유한요소해석
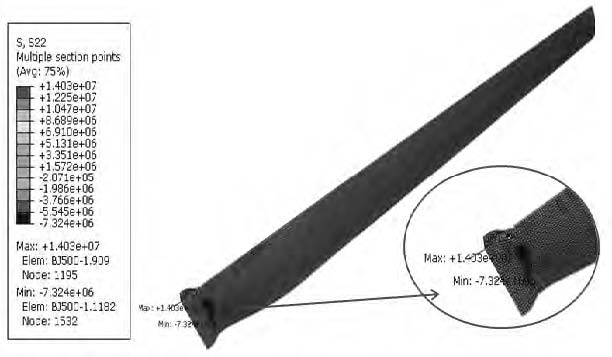
블레이드의 피로취약지점을 확인하기 위하여 공력해석을 통해 획득한 하중을 적용한 절점하중 구조해석을 수행하였다. 이의 결과는 Fig. 6에 나타내었으며, 그림에서 알 수 있듯이 구간 2에서 가장 큰 응력이 발생하였으며 이는 블레이드의 적층 두께 및 형상의 변화 때문인 것으로 판단된다. 여기서 0˚는 각 플라이의 섬유 방향, 90˚는 이에 직각인 모재 방향을 의미한다. 피로손상의 발생 가능성이 가장 높은 피로취약지점 즉, FCL의 위치 선정을 위하여 0˚ 및 90˚ 방향의 응력에 대해 평가한 결과를 Table 3에 나타내었으며, 이를 통하여 4개소의 FCLs가 확인되었다. 여기서 0˚ 및 90˚ 방향의 응력은 in plane principal 및 transverse stress를 의미한다.
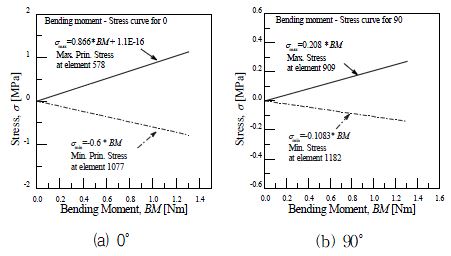
또한, 상기의 FCLs에서의 피로응력 스펙트럼을 산출하기 위하여 수행한 단위하중 구조해석의 결과는 Table 4에 나타내었으며, 이는 절점하중 구조해석을 통하여 확인한 피로취약지점에 대한 응력이다. 이를 이용하여 식 (6)과 같이 굽힘 모멘트-최대 및 최소 응력의 상관 관계식을 구하였으며 Fig. 7은 이의 결과를 나타낸 것이다. 이 때, 음의 수는 압축응력의 의미를 가진다.
여기서 A 및 B 는 상수이다.
3.5. 피로 저항성 평가
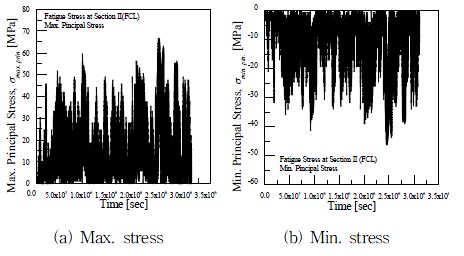
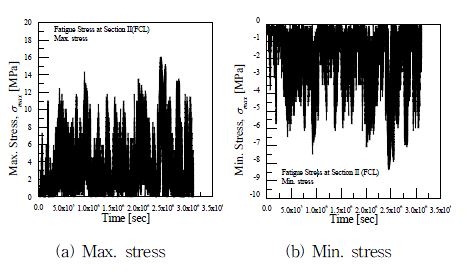
피로 저항성 평가를 위해서는 피로취약지점에서의 피로응력 스펙트럼이 필요하다. 그러므로 굽힘 모멘트-응력 곡선 (Fig. 7)을 통하여 획득한 식 (6)에 굽힘 모멘트 스펙트럼 (Fig. 4)을 적용하여 산출하였으며, 이의 결과로는 Fig. 8 및 9에 섬유 방향 및 모재 방향의 피로응력 스펙트럼으로 나타내었다. 이는 불규칙한 특성을 가지고 있으므로 Rainflow cycle counting을 적용하여 정량화하였다. 또한, 평균응력을 고려하기 위하여 식 (4)를 이용하여 응력비 R=-1로 변환하였다. 이러한 결과를 GL 규격의 수명 계산식인 식 (7)에 적용하여 응력 레벨에 대한 피로 수명을 산출하였다.
여기서 Rk,t 는 인장강도, Rk,c는 압축강도,
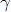 Ma는 정적 강도의 안전계수,
Ma는 정적 강도의 안전계수,
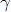 Mb는 피로강도의 안전계수, σk,m 은 평균응력, σ k,m는 응력진폭, Clb는 N1/m , m은 S-N 곡선의 기울기이다(Table 6 참조).
Mb는 피로강도의 안전계수, σk,m 은 평균응력, σ k,m는 응력진폭, Clb는 N1/m , m은 S-N 곡선의 기울기이다(Table 6 참조).
이러한 응력을 식 (8)의 Miner’s rule을 적용하여 블레이드의 총 손상량을 산출하고 비교하였다.
여기서 Ni 는 응력 범위에 대한 피로수명이며, ni 는 응력 범위에 대한 하중 반복수를 나타낸다.
응력 범위에 대한 하중 반복수를 획득하기 위하여 평균 응력 및 응력 범위에 따라 하중 반복수를 정리한 Markov matrix를 획득하였으며, Table 5는 모재 방향 최대 응력의 경우를 나타낸 것이다. 또한, 변수들 중 S-N 곡선의 기울기인 m은 GL 규격에서 10으로 정의되어있지만 실제로 시험한 피로시험 데이터를 이용해 산출하였을 때, 0˚의 경우 8.94, 90˚의 경우 8.32 가짐을 알 수 있었다. 이를 통하여 두 가지 경우에 대하여 블레이드의 피로 손상량을 획득하였다.
Fig. 8 및 9의 피로응력 스펙트럼을 식 (7)에 적용하여 복합재 블레이드의 피로 손상량을 계산한 결과를 Table 7에 나타내었다. 이를 통하여 최대 2.55E-4의 손상량이 평가되었으며 상당히 낮은 수준의 손상량으로서 이의 원인은 Fig. 3에서 볼 수 있듯이 낮은 수준의 풍속에 기인한 것으로 판단된다. 또한, 실제 S-N 자료에 의한 총 손상량이 2.55E-4인 반면에 GL 규격의 총 손상량은 3.34E-5이다. 따라서 S-N 자료에 의한 값이 더 크게 평가가 된 것으로 보아 안전설계를 위해서는 실제 피로특성 자료를 토대로 수행된 피로 저항성 평가가 필요하다고 판단된다.
4. 결 론
본 연구에서는 GL 규격에 의하여 소형 복합재 블레이드의 피로 저항성을 평가하였으며 이에 얻어진 결과는 다음과 같다.
1) BEMT를 적용하여 블레이드에 작용하는 공력하중과 풍속-굽힘 모멘트의 관계식을 도출하였다.
2) 실제 풍속을 측정하여 블레이드의 굽힘 모멘트 스펙트럼을 산출하였다.
3) 블레이드의 재료에 대하여 피로 시험을 실시하였으며 Basquin’s equation으로 이의 피로 특성을 획득하였다.
4) 유한요소해석을 수행하여 피로취약지점을 확인하였으며 굽힘 모멘트-피로취약지점의 응력 관계식을 도출하였다.
5) 굽힘 모멘트 스펙트럼과 굽힘 모멘트-응력 관계를 이용하여 피로취약지점에서의 피로응력 스펙트럼을 산출하였다. 또한, 이에 Rainflow cycle counting 및 Goodman diagram을 적용하여 정량화하였으며 GL 규격의 수명 계산식을 이용하여 설계 수명동안의 피로 손상을 평가하였다.
Acknowledgments
본 연구는 2012년도 한국에너지 기술평가원 (No. 20123021020010) 및 한국연구재단의 일반연구자지원사업(No. 2011-0007012)의 지원을 받아 수행한 연구 과제입니다.
References
- 황병선, “최신 풍력 터빈의 이해”, 아진, (2010), p145.
- 최정훈, 강민성, 박홍선, 구재민, 석창성, “충격손상을 받은 항공기용 복합재료의 잔류강도 변화에 따른 피로수명 특성 평가”, 대한기계학회 재료 및 파괴부문 학술대회, (2010), p53-59.
- 음학진, 남현우, 김만응, “IEC 61400-1 DLC.1.1에 따른 풍력터빈의 극한하중”, 대한기계학회 춘추학술대회, (2010), p3648-3653.
- 박성완, “인장-비틀림 하중에 의한 섬유강화 복합재료의 피로수명 예측”, 한국생산제조시스템학회, (2004), 13(6), p64-73.
-
기영중, 김승호, 한정호, 정재권, 허장욱, “손상된 복합재 로터 블레이드의 고주기 피로수명 평가”, 대한기계학회, (2012), 36(10), p1275-1282.
[https://doi.org/10.3795/KSME-A.2012.36.10.1275]

-
Kong, C.D., Kim, T.H., Han, D.H., Sugiyama, Y, “Investigation of fatigue life for a medium scale composite wind turbine blade”, International Journal of Fatigue, (2006), 28, p1382-1388.
[https://doi.org/10.1016/j.ijfatigue.2006.02.034]

- Spera, D.A, “Dynamic loads in horizontal-axis wind turbines part II : empirical equation”, Windpower’93, (1993), p282-289.
-
Ronold, K.O., Wedel-Heinen, J., Christensen, C.J, “Reliability-based fatigue design of wind-turbine rotor blades”, Engineering Structures, (1999), 21, p1101-1114.
[https://doi.org/10.1016/S0141-0296(98)00048-0]

- Miner, M.A, “Cumulative Damage in Fatigue, Journal of Applied Mechanics”, (1945), 12, pA159-A164.
-
Wu, J.H., Lai, F.M, “Fatigue Life Analysis of Small Composite Sandwich Wind Turbine Blades”, Procedia Engineering, (2011), 14, p2014-2020.
[https://doi.org/10.1016/j.proeng.2011.07.253]

- International Standard, IEC 61400-2, “Design requirements for small wind turbine”, Second edition, (2006.).
-
Epaarachchi, J.A., Clausen, P.D, “The development of a fatigue loading spectrum for small wind turbine blades”, Journal of Wind Engineering and Industrial Aerodynamics, (2006), 94, p207-223.
[https://doi.org/10.1016/j.jweia.2005.12.007]

- Lloyd, Germanischer, “Rules and regulations IV-NonMarine Technology, Part I-wind energy”, (1999.).
- PROPID Version 5.1, University of Illinois at Urbana-Champaign, (2007.).
- ABAQUS Version 6.10, Dassault Systemes Simulia, (2010.).
- J.A. Bannantine, Comer, J.J., Handrock, Fundamentals of metal fatigue analysis, New Jersey : Prentice-Hall, (1990.).