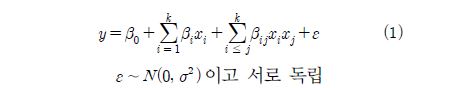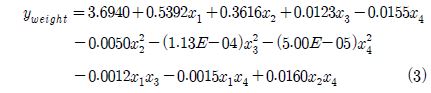Structural Optimization for Small Scale Vertical-Axis Wind Turbine Blade using Response Surface Method
The purpose of this paper is to perform the structural design of the small scale vertical-axis wind turbine (VAWT) blade using a response surface method(RSM). First, the four design factors that have a strong influence on the structural response of blade were selected. Analysis conditions were calculated by using the central composite design(CCD), which is a typical design of experiment for the response surface method(RSM). Also, the significance of the central composite design(CCD) was verified using analysis of variance(ANOVA). The finite element analysis was performed for the selected analytical conditions for the application of response surface method(RSM). Finally, a optimization problem was solved with a objective function of blade weight and a constraint of allowable stress to achieve a optimal structural design of blade.
Keywords:
Blade, Central Composite Design, Response Surface Method, Optimized Structural, Vertical-Axis Wind Turbine, 블레이드, 중심합성계획법, 반응표면법, 구조 최적화, 수직축 풍력발전기1. 서 론
풍력발전기(Wind turbine)는 바람이 가지는 운동에너지를 전기 에너지로 변환하는 방식으로 로터 블레이드(Rotor blade)와 회전축의 형상에 의해 수직축 풍력발전기(Vertical- Axis Wind Turbine, VAWT)와 수평축 풍력발전기(Horizontal- Axis Wind Turbine, HAWT)로 구분된다.(1) 일반적으로 수직축 풍력발전기는 수평축 풍력발전기보다 효율이 낮고, 작동범위가 적다는 단점을 가지고 있지만, 바람 방향에 무관하게 작동되고, 시동풍속(Cut-in speed)이 낮은 특성은 풍향의 변화가 심하고, 주로 낮은 풍속의 분포를 보이는 우리나라에서 적절한 풍력발전기로 사료된다.(2)
대부분의 수직축 풍력발전기의 블레이드는 가공의 용이성과 경제성의 이유로 금속재료를 사용하고 있으며, 이를 이용하여 설계 및 제작된 블레이드는 종류 및 용량에 따라 상이하지만 크게 전단 웹(Shear web), 스파 캡(Spar cap), 상부 면(Suction side) 및 하부면(Pressure side) 등의 구조요소로 이루어진다. 여기서 전단 웹과 스파 캡은 박스 빔(Box beam)을 구성하여 대부분의 굽힘하중(Bending load)과 전단하중(Shearing load)을 지지하는 역할을 하며, 상부 면과 하부 면은 공력하중과 일부 구조 하중을 함께 지지하는 역할을 한다. 이러한 구조요소를 고려한 수직축 블레이드 강도설계에 관한 연구로는 블레이드에 대한 구조해석(Structural analysis), 피로해석(Fatigue analysis) 및 좌굴해석(Buckling analysis) 등이 있다.(3)
예를 들어, 김동현 등(4)은 6kW급 수직축 풍력발전기에 대하여 공력하중해석, 성능해석, 구조해석, 진동해석을 수행하였다. 조우석 등(5)은 1kW급 자이로밀형 수직축 풍력터빈에 대하여 유동해석, 구조해석을 수행하였다. 상기 연구들에서 알 수 있듯이 대부분의 연구가 블레이드의 전체적인 반응을 고려한 구조설계와 해석에 집중되어 있으며, 복수이상의 블레이드의 구조요소를 고려한 연구는 거의 없는 실정이다.
한편 위에서 언급하였듯이 블레이드의 하중지지 요소로는 스파 캡, 스파 캡 두께 및 전단 웹 두께 등을 들 수 있으며 블레이드의 구조적 건전성을 확보하기 위해서는 이러한 구조요소를 동시에 고려하여야 한다. 이처럼 설계변수가 여러 개일 경우, 이들의 반복해석을 최소화(Minimize)하고 설계변수 간의 상호작용을 평가하기 위한 방법으로 대표적인 것이 반응표면법(Response Surface Method, RSM)이다. 반응표면법은 1950년대에 Box와 Willson과 여러 연구자에 의해 통계분야에서 처음으로 개발된 이후 통계 분야에서 반응표면을 구성하기 위한 다양한 연구가 진행되었다.(6) 박정선 등(7)은 반응표면법에 의한 인공위성 구조체의 최적설계를 수행하였다. 임표 등(8)은 반응표면법을 이용한 5축 임펠러 정삭 가공의 최적화를 수행하였다. 이후로도 많은 연구가 다양한 분야에서 반응표면법을 이용하여 적용하고 있지만, 수직축 풍력터빈 블레이드의 구조 최적화에 적용한 사례는 전무한 실정이다.
본 연구에서는 소형 수직축 풍력발전기에 사용되는 블레이드를 대상으로 구조적 안전성에 영향을 주는 설계 인자의 최적화에 대하여 고찰하였다. 설계 인자는 전단 웹 두께, 스파 캡 두께, 전단 웹 위치(Shear web position) 및 전단 웹 간격(Shear web spacing)이며 목적함수(Objective function) 및 제한조건(Constraint)은 각각 중량 및 허용응력(Allowable stress)으로 설정하여 이에 대한 반응표면법을 적용하였다. 또한, 응력 및 중량에 대한 설계 인자의 영향을 나타내는 민감도 해석(Sensitivity analysis)을 수행하였다.
2. 해석방법
2.1. Blade
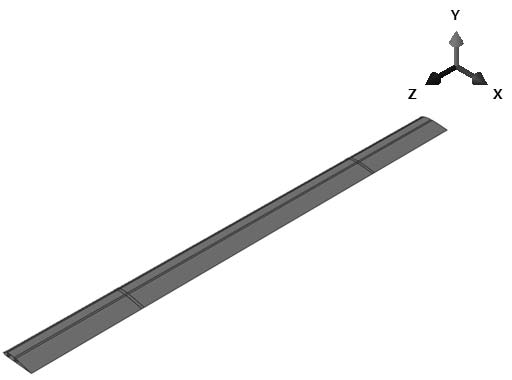
본 연구의 대상이 되는 수직축 블레이드는 정격 풍속 10m/s, 정격 용량 3kW의 소형 풍력발전기로서 금속재질인 A6063-T5를 사용하였으며, 기계적 물성은 Table 1(9)와 같다. Table 2은 블레이드의 기본 설계사양을 나타낸 것이며, 블레이드의 3차원 형상은 Fig. 1과 같다.
블레이드는 불규칙한 바람 및 원심력에 의하여 다양한 하중조건에 놓이게 되는데 현재까지는 수직축 풍력터빈 블레이드에 대한 안전계수(Safety factor)가 정립되지 않은 상황이다. 따라서 소형 수평축 풍력발전기의 설계 표준 규격인 IEC 61400-2에 의거하여 안전계수를 3.3으로 선정하였다.
2.2. 반응표면법
반응표면법은 여러 개의 독립변수 x1 , x2 , ··· , xk 가 복합적인 작용을 함으로써 어떤 종속변수 y에 영향을 주고 있을 때 이러한 반응의 변화가 이루는 반응표면에 대한 통계적인 분석방법을 말한다.(10)
반응표면 생성 시에 독립변수와 종속변수 간의 관계를 정확하게 파악하기란 거의 불가능하므로 여러 가지 후보 함수 중에서 적절한 것을 선택하여야 한다. 본 연구에서는 회귀계수를 구하기 쉽고 모델형태가 유연하며 이미 많은 문제에서 적용된 독립변수의 수가 k인 2차 회귀모형 식(1)을 사용하였다.
여기서 y는 반응치, β0, β1, β2는 회귀상수, xi, xj는 독립변수이다. 또한 ε 은 반응치의 오차항이며 N(0, σ2)은 샘플자료에서 추정한 출력 값이 N이면서 평균이 0이고 분산 σ2을 가지는 정규분포를 따른다는 의미이다.
그러나 비선형적인 변화를 감지할 수 없는 심플렉스계획법이나 2k요인배치법 등으로는 회귀계수를 추정할 수 없기 때문에 단점을 보완하고 적은 횟수의 실험으로 곡면을 추정하기 위하여 중심점과 축점을 2k 요인실험에 추가시킨 실험계획법인 중심합성계획법(Central Composite Design, CCD)을 사용하였다.(10)
2.3. 구조해석 방법
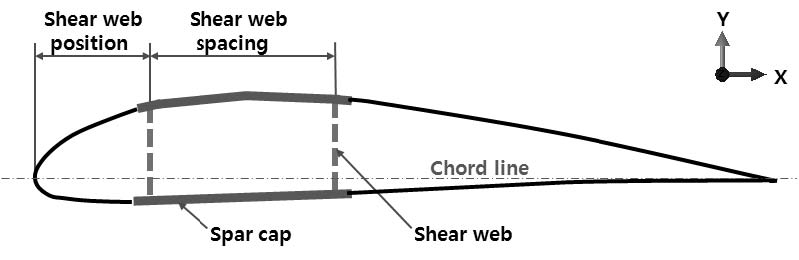
수직축 블레이드의 구조 안전성을 평가하기 위해 상용 소프트웨어인 ABAQUS(11)를 사용하여 제한조건 및 목적함수인 응력 및 중량에 대하여 평가하였다. 독립변수는 Fig. 2에 나타내었으며, 그림에서 확인할 수 있듯이 4인자(전단 웹 두께, 스파 캡 두께, 전단 웹 위치, 전단 웹 간격)를 선정하였다.
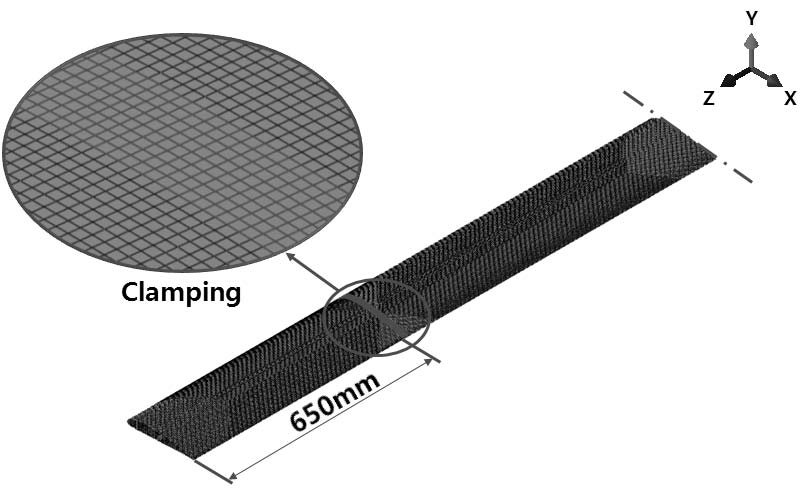
블레이드의 구조해석을 수행하기 위하여 회전 시 지지대를 부착한 구조를 Fig. 3과 같이 묘사하였으며, 블레이드 끝단 650mm지점부터 Z 방향으로 16mm 두께로 클램핑(Clamping) 시켰다. 적용되는 경계조건은 클램핑 부분의 X, Y, Z 방향 및 X, Y, Z 회전방향(Rotation direction)의 자유도를 구속하였으며, 작용하는 하중은 블레이드가 회전할 때 원심가속도(Centrifugal acceleration)에 의하여 발생되는 하중을 블레이드 전체에 적용하였다.
블레이드의 형상은 두께 방향의 치수가 다른 치수에 비하여 상당히 작기 때문에 Fig. 3과 같은 쉘 요소(Shell element)로 모델링 하였다. 전체 유한 요소 모델은 쉘 요소 중에서 4절점을 가진 S4R이 사용되었으며 요소(Element)의 개수는 181,168개이고, 절점(Node)의 개수는 179,191개이다.
3. 결과 및 고찰
3.1. 초기조건
블레이드 4인자의 초기조건은 Table 3과 같이 나타내었으며, Fig. 4는 블레이드 4인자의 초기조건에 따른 해석 결과이다. 표 및 그림에서 알 수 있듯이 안전계수 3.3을 고려한 허용응력 56.36MPa보다 큰 65.01MPa이라는 응력이 클램핑 부근 전단웹과 스파캡의 접합부에서 발생하였으며, 4가지 설계인자의 초기조건으로는 구조 안전성 조건을 만족하지 못함이 확인되었다.
3.2. 해석결과
초기 해석결과 블레이드의 응력이 허용응력 56.36MPa을 초과하였으므로 반응표면법을 이용하여 이를 허용응력이하로 유지한 상태에서 중량을 최소화하기 위하여 상용 소프트웨어인 MINITAB(12)을 사용하여 해석조건(Analysis conditions)을 산출하였다.
Table 4는 4인자에 대한 중심합성계획법의 실험배치(Design matrix)를 나타낸 것이다. 중심합성계획법의 독립변수가 k라면 회전성(Rotatability)을 유지해주는 α 값은 2k/4라는 식을 이용하여 중심합성계획법이 바람직한 성질을 갖도록 α = 2로 설정하였다.
실험 점의 수는 요인실험점 2k, 축점 2k, 중심점 nc를 사용하여 2k + 2k + nc와 같이 나타내었으며, 중심점 nc은 실험결과의 신뢰도를 높이기 위해 7번의 반복실험을 수행하였다. 총실험 횟수는 4인자의 변화에 따른 응력 및 중량의 변화를 고려하여 31회의 실험 점을 선택하였다. 초기조건 4인자를 바탕으로 인자 수준의 재배치를 위해 중심합성계획법을 사용하였으며, 유의성(Significance)을 검증하기 위하여 분산분석(Analysis of variance, ANOVA)을 사용하였다.
Table 5는 블레이드의 4인자에 대한 응력을 제한조건으로 하는 2차 회귀모형(Regression model)의 유의성을 검증하기 위하여 분산분석한 결과이다. 표에서 확인할 수 있듯이 DF는 독립변수의 자유도, Seq SS 와 Adj SS는 그룹 간 요인 제곱합 및 그룹 내 오차 제곱합, Adj MS는 제곱합을 자유도로 나눈 평균 제곱, F는 요인 MS를 오차 MS로 나눈 값이다. 또한 P는 랜덤 오차를 통해 관측된 값과 가설된 값 사이의 차이와 크기가 같은 차이를 얻을 수 있는 확률로 0.05보다 작으면 해당 요인을 유의하다고 판단한다. 추정된 회귀모델의 계수를 살펴보면 1차, 2차 및 교호작용 항의 계수 중에서 P 값이 0.05보다 큰 유의하지 않은 계수도 있지만, 추정모델의 1차, 2차 및 교호작용항의 곡면이 유의하거나 무시할 수 없어 모두 사용하였으며 오차항(Error term)의 경우 Table 4에서 No. 25∼31까지 7번의 순수반복 실험이 전산실험이기 때문에 오차가 없으며 이때의 추정된 회귀방정식(Regression equation)의 결정계수 R2는 95.45%로 블레이드에 작용하는 응력을 추정하는데 적합하다고 할 수 있다.
따라서 식 (2)와 같이 2차 회귀방정식을 추정하였다.
Table 6은 블레이드의 4인자에 대한 중량을 목적함수로 하는 2차 회귀모형의 유의성을 검증하기 위하여 분산분석한 결과이다. 추정된 회귀모델의 계수를 살펴보면, 1차 항의 계수는 모두 0.05 이하로 유의함을 증명하였으며, 2차 및 교호작용항의 계수 중에서 P 값이 0.05보다 큰 유의하지 않은 계수는 오차항으로 풀링(Pooling)하였으며, 이때의 추정된 회귀방정식의 결정계수 R2는 100%로 블레이드의 중량을 추정하는데 적합하다고 할 수 있다. 이에 식 (3)과 같이 2차 회귀방정식을 추정하였다.
안전계수를 만족하고 중량을 최소화할 수 있는 4인자의 설계조건(Design conditions)들을 찾기 위하여 반응 최적화 도구를 사용하였고, Table 7은 반응 최적화 도구를 사용한 결과이다. 응력은 초기조건 65.01MPa 보다 약 14% 감소한 55.86MPa로 안전함을 확인하였고, 중량은 초기조건 6.19kg보다 약 9.37% 증가한 6.83kg의 결과를 얻을 수 있었다.
3.3. 민감도 해석
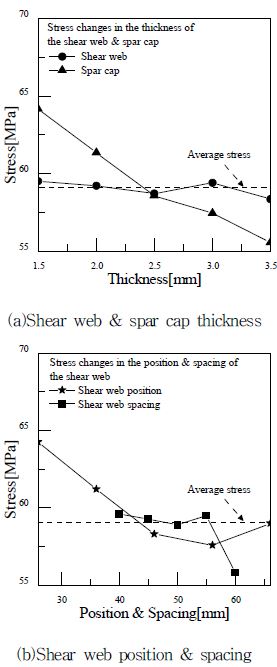
수직축 풍력터빈 블레이드의 4인자가 목적함수인 응력 및 중량에 미치는 영향을 알아보기 위하여 민감도 해석을 수행하였다. Fig. 5는 응력에 대한 민감도 해석 결과를 타나낸 것이며 그림에서 확인할 수 있듯 이 Fig. 5(a)에서는 전단 웹의 두께 변화에 따른 응력에는 영향이 크지 않았고, 스파 캡의 두께가 증가함에 따라 응력이 감소하였음을 확인하였다. Fig. 5(b)에서는 전단 웹의 위치가 56.06mm까지 증가함에 따라 응력이 감소하였으며, 그 이후부터는 응력 값이 증가함을 확인하였다. 전단 웹의 간격이 55mm에서 60mm로 증가함에 따라 응력 값이 급격히 감소함을 확인하였다.
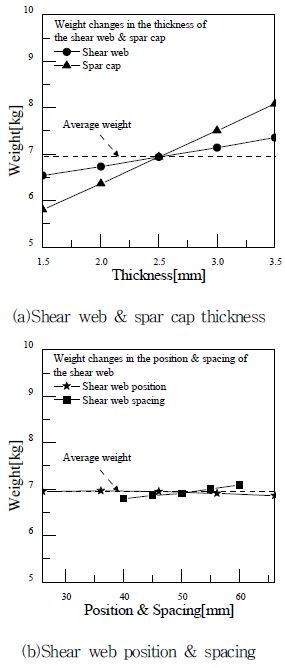
중량에 대한 민감도 해석 결과를 Fig. 6과 같이 나타내었으며, 그림에서 볼 수 있듯이 Fig. 6(a)에서는 전단 웹 및 스파 캡의 두께가 증가함에 따라 중량이 증가하였으며, 스파 캡의 두께변화가 전단 웹의 두께 변화보다 중량에 영향을 크게 미침을 확인하였다. Fig. 6(b)에서 전단 웹의 위치변화에 따른 중량에 미치는 영향은 미미하였으며, 전단 웹의 간격이 증가함에 따라 중량이 증가함을 확인하였다. 민감도 해석을 통하여 응력 및 중량에 영향을 미치는 인자를 확인할 수 있었다.
4. 결 론
본 연구는 반응표면법을 이용하여 소형 수직축 블레이드의 구조적 안전성에 영향을 미치는 설계 인자의 최적화에 대한 연구를 수행하였다. 이에 얻어진 결과는 다음과 같다.
1) 블레이드의 구조적 안전성에 영향을 미치는 4인자로 전단 웹 두께, 스파 캡 두께, 전단 웹 위치 및 전단 웹 간격을 선정하였으며, 이들의 응력 및 중량에 대한 연관성을 확인하였다.
2) 중심합성계획법을 이용하여 실험 횟수를 31번으로 최소화시켰으며 분산분석을 통하여 유의성의 검증을 확인하였다.
3) 반응 최적화 도구를 사용하여 응력을 허용응력 이하로 유지한 상태에서 중량을 최소화할 수 있는 4인자의 설계조건을 찾을 수 있었다.
4) 중량 증가를 최소화한 상태에서 초기조건인 65.01MPa보다 약 14% 감소한 55.86MPa의 응력이 발생하여 구조적 안전성을 확인하였다.
5) 민감도 해석을 통하여 응력 및 중량에 크게 영향을 주는 인자를 확인할 수 있었다.
Acknowledgments
본 연구는 2012년도 지식경제부의 재원으로 한국에너지 기술평가원(KETEB)의 지원을 받아 수행한 연구 과제(No.20123021020010 및 No.20124010203240)입니다.
References
- Oh, Y.I., “Evaluation of Structural and Vibrational Properties of Vertical Axis Wind Turbine Blade”, Korea Society for Precision Engineering Fall Conference Proceedings, (2010), p767-768.
-
Jeong, J.H., Kang, K.W., Kim, B.S., Lee, J.H., “Effect of Geometric Variation on Starting Characteristic Analysis of H-Darrieus Blades”, Fluid Machinery Research and Development Conference, (2010), p356-361.
[https://doi.org/10.5293/KFMA.2011.14.3.045]

- Lee, S.P., Kang, K.W., Jang, S.M., Lee, J.H., “Structural Design and Analysis for Small Wind Turbine Blade”, Korean Journal of Machine Tools, (2010), p288-294.
-
Kim, D.H., Choi, H.C., Lee, J.W., Ryu, G.J., Kin, S.B., Kim, K.W., Nam, H.W., Lee, M.G., “Aerodynamic and Structural Design of 6kW Class Vertical-Axis Wind Turbine”, Fluid Machinery Research and Development Conference, (2010), p273-280.
[https://doi.org/10.5293/KFMA.2011.14.2.052]

- Cho, W.S., Kim, H.S., Choi, Y.D., “Flow and Structural Analysis on the 1kW-Class Gyromill Type Vertical Axis Wind Turbine”, Wind Energy Journal, (2010), 1(2), p53-58.
-
Box, G., Wilson, K., “On The Experimental Attainment of Optimum Condition”, Journal of Royal Statical Society, Ser. B, (1951), 13, p1-45.
[https://doi.org/10.1007/978-1-4612-4380-9_23]

- Park, J.S., Yoon, J.H., Im, J.B., “Optimal Disign of a Satellite Structure by Response Surface Method”, Korean Society for Aeronautical and Space Sciences, (2004), 32(1), p22-28.
-
Lim, P., Yang, G.E., “Optimization of Finish Cutting Condition of Impeller with Five-Axis Machine by Response Surfac Method”, Korean Society of Mechanical Engineers, (2007), 31(9), p924-933.
[https://doi.org/10.3795/KSME-A.2007.31.9.924]

- Material Property Data Home page, http://www.matweb.com(April, 01, 2012), A6063-T5.
- Park, S.H., “Modern Design of Experiments”, MINYOUNGSA, (2003.).
- ABAQUS Version 6.10, Dassault Systemes Simulia, Inc.2010.
- MINITAB Version 16, Inc.2010.