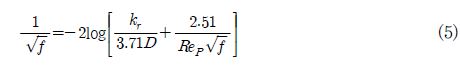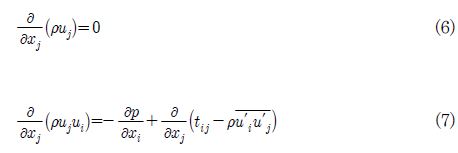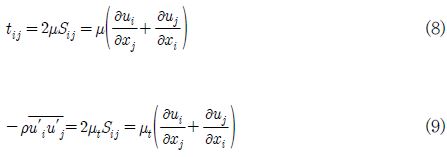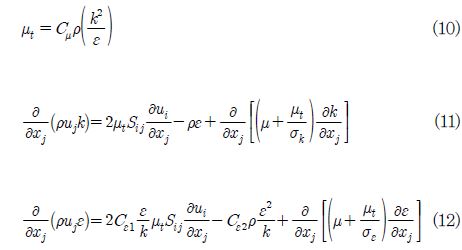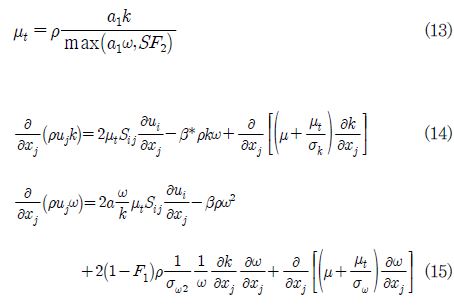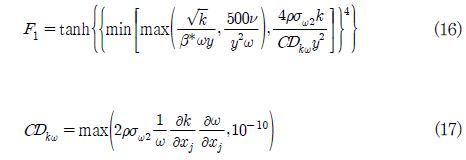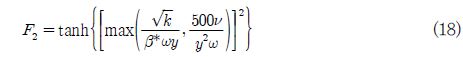Numerical Study of the Averaging BDFT(bidirectional flow tube) Flow Meter on the Applicability in the Fouling Condition
Most of the nuclear power plants(NPPs) adopts pressure difference type flow meters such as venturi and orifice meters for the measurement of feedwater flow rates to calculate reactor thermal power. However, corrosion products in the feedwater deposits on the flow meter by fouling as operating time goes. These effects lead to severe errors in the flow indication and then determination of reactor thermal power. The averaging BDFT, which has developed by Yun et al., has a potentiality to minimize this problem thanks to its inherent measurement principle. Therefore, it is expected that the averaging BDFT can replace the venturi meter for the feedwater pipe of steam generator of NPPs. The present work compares the amplification factor, K, based on CFD calculation against the K obtained from experiments in order to confirm whether a commercial CFD code can be applicable to the evaluation of characteristic for the averaging BDFT. In addition to this, the simulations to take into account of fouling effect are also carried out by rough wall option. The results show that the averaging BDFT is a promising flow meter for the accurate measurement of flow rates in the fouling condition of the NPPs.
Keywords:
Amplification factor, Averaging bidirectional flow tube, Computational fluid dynamics, Nuclear power plant, Fouling, 압력 증배 계수, 평균 양방향 유동 튜브, 전산유체역학, 원자력 발전소, 파울링1. 서 론
원자력 발전소는 설계기준에 근거하여 원자로의 열출력을 제어한다. 안전성 측면에서는 열출력을 설계기준보다 낮게 운전하는 것이 바람직하지만 경제적인 측면에서는 최대한 설계기준에 근접하게 운전하는 것이 유리하다. 그러므로 원자로 열출력을 정확히 측정할 수 있어야 발전소의 안전성 및 경제성을 보장받을 수 있다. 국내에서 가동 중인 원자력 발전소의 원자로 열출력은 증기발생기 2차측으로 공급되는 주급수(feedwater)의 온도 차 및 유량 측정값을 이용하여 열평형 방정식으로부터 계산된다. 그러므로 원자로 열출력을 정확하게 예측하기 위해서는 주급수 유량의 정밀한 측정이 필요하다. 일반적으로 가압경수로형 원전의 주급수 유량은 원자로 2차 계통 주급수 배관에 설치된 벤투리 유량계(venturi flowmeter)를 통하여 측정된다. 벤투리 유량계는 차압식 유량계 중 정밀도가 가장 높으나 파울링(fouling)에 의해 측정 오차가 발생될 수 있다. 파울링은 미세 입자 부유물이 배관 벽면 등에 침전되어 표면 거칠기와 같은 표면 상태를 변화시키는 현상으로 이를 방지하기 위해서는 유량계의 주기적인 세정 및 교정이 필요하다. 실제로 원자력 발전소에서 벤투리 유량계의 사용 시간이 경과함에 따라 벤투리 목(throat)에 스케일이 생기는 현상이 발생하여 매년 1% 정도의 유량이 증가되고 따라서 원자로의 발전량을 줄여야 하는 문제가 보고되기도 했다.(1) 이러한 문제점을 해결하기 위해 최근에는 초음파 유량계를 원자력 발전소2차 계통 주급수 유량 계측에 적용하는 연구가 이루어지고 있다.(2) 그러나 초음파 유량계는 전자기기의 신뢰성 문제가 제기되어 미국에서는 운전 중 원전의 벤투리 유량계 재 교정에만 국한하여 사용되고 있다.
Yun et al.에 의해 개발된 평균 양방향 유동 튜브(bidirectional flow tube, BDFT)를 이용한 차압식 유량계는 사용 유체와 작동 온도, 압력의 제한이 없고 상대적으로 벤투리 유량계에 비하여 파울링에 덜 민감하게 유량 측정이 가능함으로 기존 벤투리 유량계를 대신할 수 있을 것으로 판단된다.(34) Yun et al.은 평균 양방향 유동 튜브를 이용한 유량계를 상업적으로 이용 가능하게 하기 위해 실험을 통하여 유량계의 특성 및 압력 증배 계수(amplification factor)를 평가하였다.(34) 그러나 유량계가 파울링에 무관하게 정확한 유량을 측정할 수 있음을 실험적으로 보이진 못했다. 이는 사용 유체를 지속적으로 오염시켜야 하는 등의 문제로 실험을 통해 파울링 영향을 정량화하기가 어렵기 때문이다. 반면 전산유체역학(computational fluid dynamics, CFD) 해석을 활용한다면 양방향 유동 튜브를 이용한 유량계의 유동 특성 및 파울링 영향을 정량적으로 평가할 수 있을 것으로 판단된다. Kim과 Park은 급격 확대, 축소 및 오리피스 배관의 압력 강하 특성을 전산유체역학 해석을 통해 평가하였으며 해석결과가 배관 내 압력 강하 및 Idelchik이 제안한 이론적 압력 손실 계수(pressure loss coefficient)를 잘 예측할 수 있음을 보였다.(5) Gan과 Riffat 또한 디퓨저, 오리피스 및 다공판(perforated plate)과 같은 배관 구성 요소에 대한 실험 및 해석을 통해 전산유체역학 코드가 압력 강하 및 압력 손실 계수 평가에 성공적으로 활용될 수 있음을 보였다.(67)
본 연구에서는 상용 전산유체역학 코드인 STAR-CCM+8.02를 사용하여 평균 양방향 튜브를 이용한 유량계의 유동 특성을 해석하고 유량계의 교정 커브에 해당하는 압력 증배 계수 예측 성능을 평가하고자 하였다. 또한 파울링에 의한 압력 도관(pressure tap)주위의 오염물 흡착을 모사하기 위해 유동 튜브 주위의 표면 거칠기를 변경시키며 해석을 수행하였다. 파울링은 미세 입자 부유물이 압력 도관에 침전되는 현상이므로 평균 양방향 유동 튜브를 이용한 유량계의 압력 도관이 위치하는 유동 튜브 주위에 임의의 표면 거칠기를 적용하는 해석 방법이 타당할 것으로 판단된다.
2. 평균 양방향 유동 튜브의 원리 및 특성
기존의 국소 양방향 튜브는 유로 내 특정한 지점의 국소 유속을 측정하기 위해 개발되었다.(89) 그러나 원자력 발전소와 같은 상업용 플랜트에서는 유로 내 평균 유속의 측정이 보다 중요하다. 그러므로 Yun et al.은 국소 양방향 유동 튜브의 원리를 이용하여 평균 유속 또는 유량의 계측이 가능한 평균 양방향 유동 튜브를 개발하였다.(34) 평균 양방향 유동 튜브의 유량 계측 원리는 피토관과 유사하다. 유동 튜브의 전단에서 측정되는 압력은 유체 유동에 의한 동압(dynamic pressure)이 포함된 총 압력(total pressure)과 동일하다. 반면 튜브 후단에서 측정되는 배압(back pressure)은 튜브 후단에서 유동에 의해 발생되는 흡입 효과로 유동장 내에서 형성되는 정압(static pressure)보다 작게 형성된다. 따라서 양방향 유동 튜브의 전, 후단에서 측정된 압력의 차이는 유동의 동압보다 약간 커지게 된다. 그러므로 튜브 전, 후단에서 측정된 차압을 기준으로 유로 내 평균 유속은 식 (1)과 같이 정의된다.
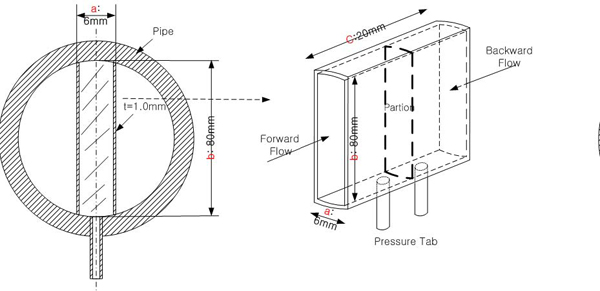
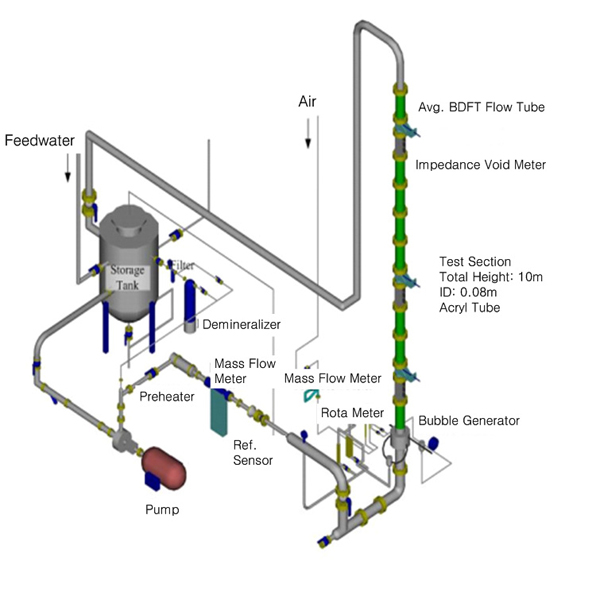
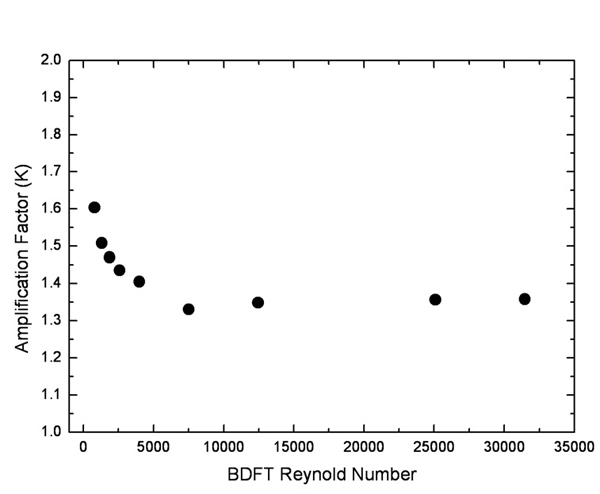
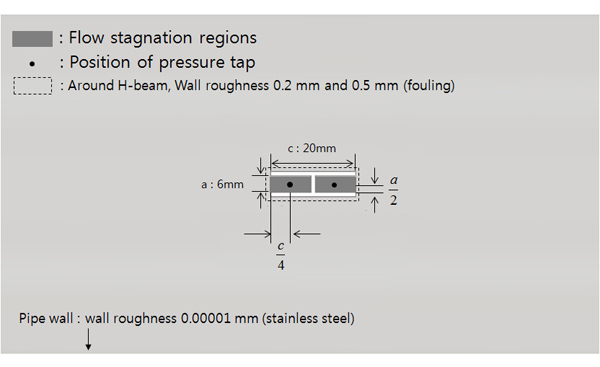
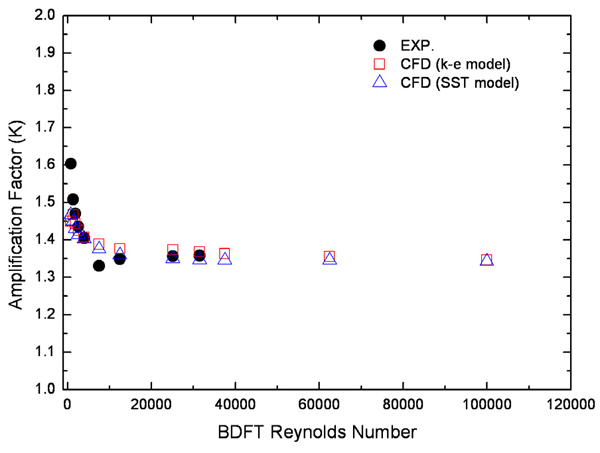
여기서, K는 압력 증배 계수이다. 이는 차압식 유량계의 송출계수(discharge coefficient)와 같이 유체의 유속에 영향을 받는 교정 상수로 실험 또는 해석을 통하여 제공되어야 한다. Yun et al.은 평균 양방향 유동 튜브의 압력 증배 계수를 얻고 유량계의 특성을 파악하기 위해 단상의 물 및 공기 유동 조건에서 교정 실험을 수행한바 있다.(34) 실험을 위해 Fig. 1과 같이 직경 80mm의 배관을 기준으로 비교적 단순화된 H-beam 형태의 평균 양방향 유동 튜브를 제작하였으며 Fig. 2와 같이 실린더형 테스트 부, 물 저장 탱크, 기포 발생기, 예열기, 물 및 공기 공급 장치, 압력 조절 장치, 계측기 그리고 데이터 취득 장치로 구성된 수직관 실험 장치에서 실험을 수행하였다. 실험은 물 및 공기를 사용하여 수행되었으나 본 논문에서는 원자력 발전소의 냉각재인 물을 사용한 실험에 국한하기로 한다. 물 실험은 2기압, 입구온도 25°C의 단열조건에서 배관 입구 평균유속을 0.06m/s∼2.5m/s로 변화하며 수행되었다. Fig. 3에 교정 실험을 통해 도출된 BDFT 레이놀즈수와 압력 증배 계수의 상관관계를 나타내었다. 압력 증배 계수는 BDFT 레이놀즈수(ReB)가 증가함에 따라 감소하는 경향을 보였으며 레이놀즈수 10,000 이상에서는 유속에 무관하게 일정함을 보였다. 이때, BDFT 레이놀즈수는 식 (2)와 같이 정의되며 레이놀즈수 계산에 사용된 수력학적 직경(hydraulic diameter, Dh)은 평균 양방향 유동 튜브의 기하학적 형상에 의하여 식 (3)과 같이 정의된다.
여기에서 V는 교정실험 시 배관 입구 평균 유속으로 이미 알고 있는 측정 값(input)이며 a, b는 양방향 튜브의 가로 및 세로 길이를 나타낸다.
3. 수치해석
3.1. 수치 계산 모델
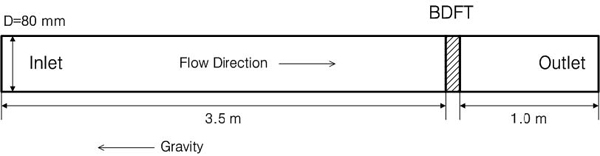
전산유체역학 코드의 압력증배계수 예측 성능을 평가하기 위하여 Yun et al.이 수행한 물 실험에 대하여 3차원 전산유체역학해석을 수행하였다. 수치해석을 위한 유동도메인은 Fig. 4와 같이 직경 80mm의 원형 배관이다. 수치해석 시 입구 유동의 완전발달을 위해서는 충분한 전단 길이(entrance length, Le) 확보가 필요하다. 본 연구에서는 식 (4)를 통하여 3.5m의 전단 길이를 확보하고 균일한 속도 분포를 갖는 유체를 주입하였다. 유동 튜브 후단은 후류의 영향을 최소화하기 위해 2m의 후단 길이를 확보하였다.
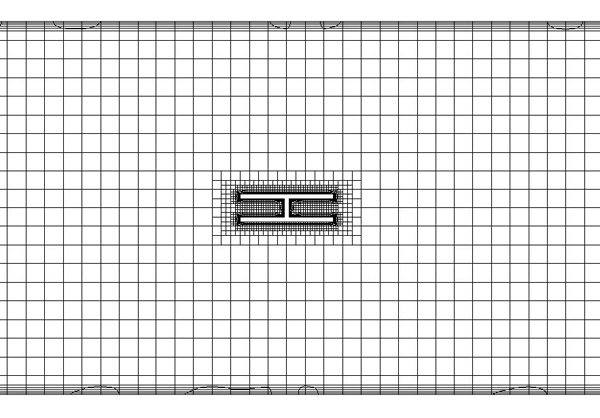
여기서, D는 배관의 직경으로 식 (4)의 관 내 레이놀즈수(ReP) 계산 시 수력직경은 배관직경을 사용하였다. 유동도메인에 Fig. 5와 같이 평균크기 4mm의 정렬격자를 생성하였으며 속도구배가 클 것으로 예상되는 평균 양방향 유동 튜브 주위에는 보다 조밀한 격자를 생성하였다. 또한 벽면 주위에는 평균격자크기의 1/10 이하인 조밀한 5개의 격자 층을 생성하였으며 총 격자수는 약 200만개이다. 이러한 격자크기 및 분포는 이들에 대한 민감도 해석결과를 바탕으로 선정한 것이다.
3.2. 수치 계산법
3차원 전산유체역학 해석은 1) 평균 양방향 튜브의 유동 특성에 대한 예측 성능을 검증하는 해석, 2) 배관 표면 거칠기 영향을 평가하는 해석 및 3) 파울링 영향을 평가하는 해석으로 구분하여 수행되었다. 1) 예측 성능 검증 해석에서는 벽면의 표면 거칠기를 매끄러운 벽(smooth wall)으로 설정하여 해석을 수행하고 해석결과 도출된 압력 증배 계수를 실험값과 비교하였다. Yun et al.(34)이 수행한 실험의 테스트 부는 아크릴 배관으로 구성되어 있으므로 수치해석 시 벽면의 표면 거칠기를 매끄러운 벽으로 설정하는 것이 타당하다. 2) 상용 배관은 재질에 따라 Table 1과 같이 고유 표면 거칠기를 가지므로 평균 양방향 유량계를 상업적으로 활용하기 위해서는 이에 대한 영향성 평가가 필요하다. 그러므로 가장 널리 사용되는 상업용 강 및 스테인리스강을 대상으로 해당 표면 거칠기를 벽면에 적용한 해석을 수행하고 이때 계산된 압력 증배 계수를 매끄러운 벽 조건과 비교하였다. 3) 파울링 영향을 평가하는 해석에서는 Fig. 6과 같이 배관 벽면에는 스테인리스강의 표면 거칠기를 적용하였으며 압력 도관이 위치하는 유동 튜브 주위에는 파울링의 영향을 모사하기 위하여 표면 거칠기를 변경하며 압력 증배 계수의 변화를 평가하였다. 표면 거칠기는 벽면의 경계조건으로 주어졌으며 이는 수치 해석계산 시 식 (5)와 같이 벽면 마찰계수(friction factor) 계산의 입력 값으로 사용된다. 여기에서, 벽면 마찰계수는 벽면 전단 응력(wall shear stress) 모델의 입력 값으로 사용된다.(1213)
여기서, f와 kr은 각각 마찰계수 및 표면 거칠기를 의미한다.
식 (6) 및 식 (7)과 같이 비압축성 유체의 정상상태 RANS(Reynolds averaged Naiver-Stokes) 방정식을 풀었으며 운동량방정식 계산 시 발생하는 압력과의 연계는 SIMPLE(semi-implicit method for pressure linked equation) 알고리즘을 사용하였다. 에너지방정식은 풀지 않았으며 대류항의 모의는 2차 풍상 차분법(2nd upwind scheme)을 사용하였다. 난류모델로는 표준 k-ε 모델, 및 SST(sheer stress transport) 모델을 사용하였다. 표준 k-ε 모델을 사용하여 난류를 모의할 시 벽함수(wall function)는 Two-Layer 방법론을 사용하였으며 SST 모델을 사용하여 난류를 모의할 시 벽함수는 High y+ Treatment 방법론을 사용하였다.(12)
여기에서 tij는 점성응력텐서(viscous stress tensor)로 식 (8)과 같이 정의되며
 는 레이놀즈응력(Reynolds stress)으로 Boussinesq 이론에 따라 식 (9)와 같이 정의된다.
는 레이놀즈응력(Reynolds stress)으로 Boussinesq 이론에 따라 식 (9)와 같이 정의된다.
표준 k-ε 모델에서 난류점성(turbulence viscosity, µt)은 식 (10)과 같이 정의되며 난류점성을 풀기 위한 난류운동에너지(turbulence kinetic energy, k) 및 난류소산율(turbulence dissipation rate, ε)의 수송방정식(transport equation)은 각각 식 (11) 및 식 (12)와 같다.
여기에서 Cµ , Cε1, Cε2, σ ε 및 σ k는 모델링 계수이며 각각 0.09, 1.44, 1.92, 1.0, 1.22의 값을 가진다. 반면 SST 모델은 k-ε 모델과 k-ω 모델의 혼합모델로 벽면 인근의 경계층(boundary layer)에서는 k-ω 모델을 통해 난류를 풀고 그 외 유동영역에서는 k-ε 모델로 난류를 모의한다. 이러한 특성으로 인하여 SST 모델은 표준 k-ε 모델과 표준 k-ω 모델에 비해 선회유동(swirl flow), 역압력구배유동(adverse pressure gradient flow), 2차 유동(secondary flow) 등 복잡한 난류현상을 보다 정확히 예측할 수 있다고 알려져 있다.(13) SST 모델의 난류점성의 정의, 난류운동에너지 및 난류소산율의 수송방정식은 각각 식 (13) 그리고 식 (14), (15)와 같다.
난류운동에너지 및 소산율의 수송방정식의 F1는 혼합함수(blending function)로 식 (16), (17)과 같이 벽면으로부터 거리의 함수이다. 점성저층(viscous layer)에서 1(k-ω 모델), 중복층(overlap layer)에서는 1 > F1 > 0의 값을 가지며 그 외 유동영역(outer layer)에서는 0의 값(k-ε 모델)을 가진다.
반면 난류점성 계산 시 필요한 2차 혼합함수 F2는 식 (18)과 같이 정의된다.
수치 계산 모델의 입구 및 출구에는 각각 유속과 압력 경계조건을 설정하였다. 입구 유속으로는 실험 유속 범위 중 최소 유속 및 최대 유속을 포함하는 9개의 모든 실험조건을 선정하여 적용하였다. 또한 높은 레이놀즈수를 가지는 유동에서 압력 증배 계수의 특성을 평가하기 위해 실험이 이루어지지 않은 유동조건인 입구평균 유속 3m/s,5m/s,8m/s 에서 추가해석을 수행하였다. 이는 각각 레이놀즈수 37,000, 62,000 및 100,000에 해당한다.
4. 수치4해석결과
4.1. 평균 양방향 튜브의 유동 특성
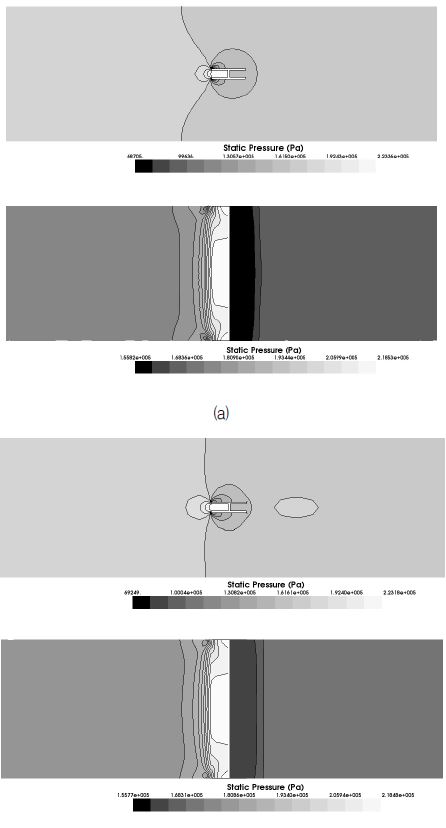
매끄러운 벽면 조건에서 전산유체역학 해석을 통해 계산된 유동 튜브 주위 압력 분포를 Fig. 7 및 Fig. 8에 나타내었다. Fig. 7은 입구 유속 0.3m/s 조건에 대한 해석결과이며 Fig. 8은 입구 유속 8.0m/s 조건에 대한 해석결과이다. 해석 결과, 유동 튜브 전단에 가장 높은 압력장이 형성된다. 반면 유동 튜브 후단에는 유동장 내 정압보다 낮은 압력(배압)이 형성되는데 이는 평균 양방향 유동 튜브의 특성인 흡입 현상을 전산유체역학 해석코드가 잘 예측하고 있음을 보여준다.
Fig. 7 및 Fig. 8과 같이 유동 튜브(H-beam) 외측의 수평방향 압력 분포(a)는 표준 k-ε 모델과 SST 모델이 다소 차이가 있으나 수직방향 압력 분포(b)는 두 난류모델의 해석결과가 유사한 결과를 보인다. 반면 압력 도관이 위치한 유동 튜브 내측 유동정체영역의 압력분포가 균일하다. 그러므로 외측의 압력분포 차이는 튜브 전, 후단 차압의 예측에는 큰 영향을 미치지 않는 것으로 판단된다. 실제 양방향 유동 튜브 유량계의 압력 도관도 H-beam 내부의 유동정체영역에 위치하고 있으므로 압력 도관의 위치가 차압의 측정에 큰 영향을 미치지 않는 것으로 알려져 있다.(89)
4.2. 압력 증배 계수
매끄러운 벽면조건에 대한 해석을 통해 도출된 평균 양방향 유동 튜브 전, 후단 압력차를 바탕으로 압력 증배 계수를 식 (19)를 통해 계산하였다.
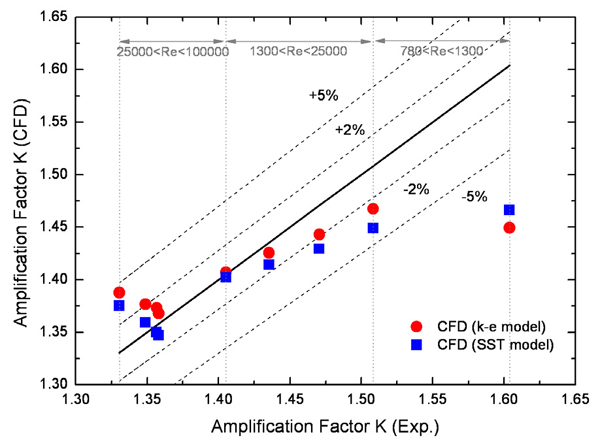
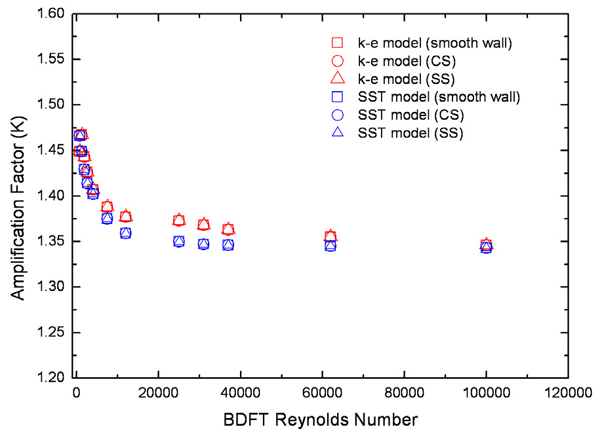
식 (19)의 차압은 Fig. 6에 나타난 압력 도관 위치에서 계산되었으며 이는 실제 제작된 유동 튜브의 압력 도관 위치와 동일하다. 물의 속도는 입구 경계에서 주어진 입구 유속을 사용하였으며 밀도는 2기압, 온도 25°C의 물의 밀도를 사용하였다. 해석을 통해 계산된 압력 증배 계수와 실험값에 근거한 압력 증배 계수를 Fig. 9에 나타내었다. 표준 k-ε 모델과 SST 모델은 레이놀즈수 1,000 이하의 낮은 레이놀즈수 유동에서는 실험결과와-9% 정도의 다소 큰 오차를 보인다. 이는 낮은 레이놀즈수 유동에서 난류모델이 가지고 있는 문제점으로 판단된다. 그러나 레이놀즈수 1,300 이상의 높은 레이놀즈수 유동에서는 압력 증배 계수를 비교적 잘 예측하고 있다. 높은 레이놀즈수 영역에서 표준 k-ε 모델과 SST 모델은 Fig. 10과 같이 레이놀즈수가 7,500인 조건을 제외하면 약 ±2%의 오차를 가진다. 레이놀즈수 1,300에서 25,000까지의 유동 영역에서는 표준 k-ε 모델이 SST 모델에 비해 상대적으로 실험결과를 잘 예측하고 있으며 레이놀즈수 25,000 이상의 유동 영역에서는 SST 모델이 표준 k-ε 모델에 비하여 실험결과를 상대적으로 잘 예측하고 있다. 표준 k-ε 모델이 SST 모델에 비하여 복잡한 난류유동 또는 역압력구배유동에 대한 예측 성능이 떨어진다고 알려져 있으나 양방향 유동 튜브 전, 후단의 압력 강하 및 튜브 후단에 발생하는 역압력구배유동은 비교적 잘 예측하고 있다고 판단된다. 또한 전산유체역학 해석결과는 레이놀즈수가 증가함에 따라 압력 증배 계수가 직진성을 보이는 압력 증배 계수의 실험적 특성을 잘 예측하고 있다.
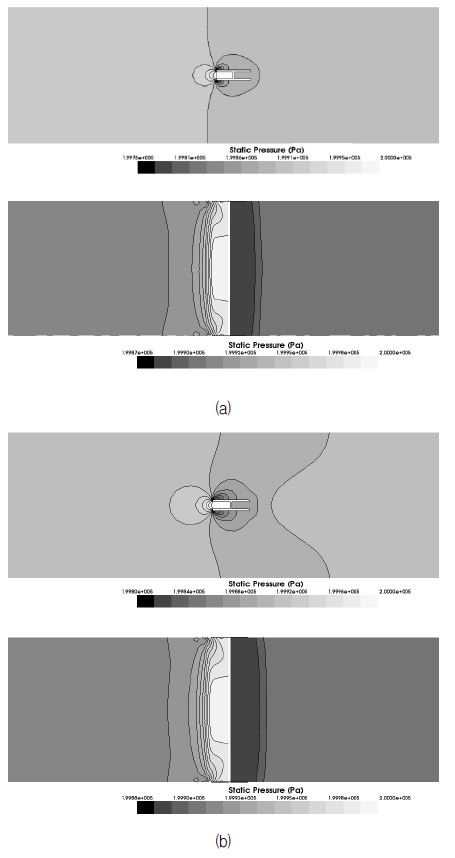
Pressure distribution around the BDFT (a) standard k-ε model (b) SST model (inlet velocity : 0.3m/s)
4.3. 표면 거칠기 영향
상용 배관은 재질에 따라 고유의 표면 거칠기를 가지므로 평균 양방향 튜브를 이용한 유량계를 상업적으로 활용하기 위하여 이에 대한 영향성 평가가 필요하다. 따라서 상업용 강 및 스테인리스강의 표면 거칠기인 0.00015mm 및 0.00001mm의 거칠기를 벽면에 적용한 전산유체역학 해석을 수행하였다. 수치 해석 모델 및 해석 방법은 벽면의 거칠기 조건을 제외하고 매끄러운 벽면 조건과 모두 동일하며 난류모델은 표준 k-ε 모델과 SST 모델을 사용하였다. 해석결과, 압력 증배 계수는 Fig. 11과 같이 벽면의 표면 거칠기에 무관하게 동일한 값을 보인다. 그러므로 평균 양방향 튜브 이용한 유량계는 상용 배관의 미세한 표면 거칠기와 무관한 압력을 측정할 수 있어 상업적으로 활용하기에 문제가 없음을 알 수 있다. 파울링의 영향이 없는 매끄러운 벽면 조건 및 거친 벽면 조건에서 평균 양방향 유동 튜브에 대한 3차원 전산유체역학 해석결과, 상용 전산유체역학 코드를 이용하여 양방향 유동 튜브의 특성 및 압력 증배 계수를 적절히 모의할 수 있음을 확인하였다. 그러므로 실험을 통해서 검증하기 어려운 파울링 영향도 전산유체역학 해석을 통해 검증할 수 있을 것으로 판단된다.
4.4. 파울링 영향
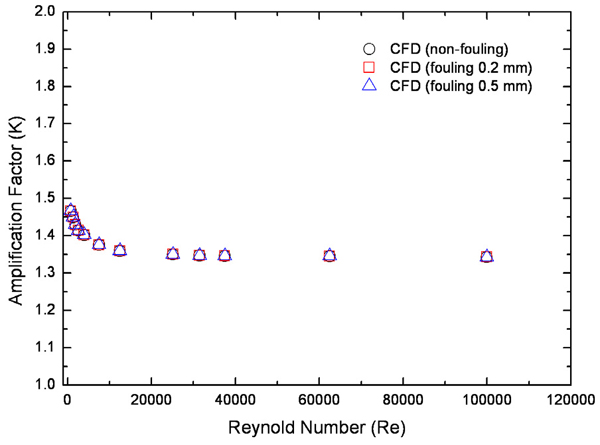
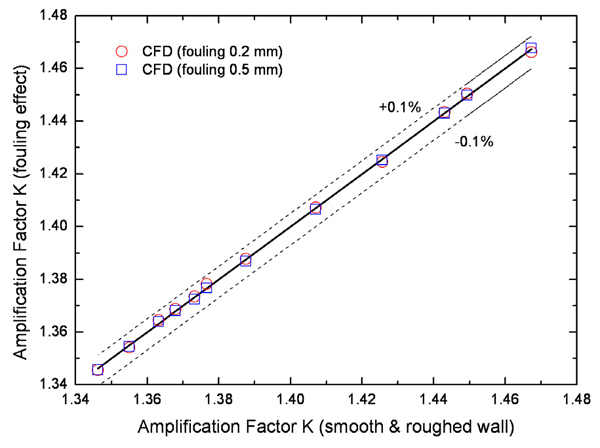
평균 양방향 유동 튜브가 파울링의 영향과 무관하게 유량을 정확히 측정할 수 있음을 검증하기 위해 유동 튜브 주위의 표면 거칠기를 변경하며 전산유체역학 해석을 수행하였다. 이는 파울링에 의하여 미세 입자 부유물이 압력 도관에 침전되는 현상을 모사하기 위함이다. 난류모델은 높은 레이놀즈수 영역에서 평균 양방향 유동 튜브의 유동 특성을 상대적으로 잘 모의하고 있는 SST 모델을 사용하였으며 수치 해석 모델 및 해석 방법은 벽면의 거칠기 조건을 제외하고 매끄러운 벽면 조건과 모두 동일하다. 배관 벽면의 표면 거칠기는 스테인리스강의 표면 거칠기인 0.00001mm를 설정하였으며 유동 튜브 주위의 표면 거칠기는 Fig. 6과 같이 파울링 영향을 고려하여 0.2 mm, 0.5mm로 선정하였다. 산업용 강의 경우, 장기사용으로 인한 부식이 발생하였을 시 약 0.15 mm∼0.4 mm의 표면 거칠기를 가지므로 본 연구에서는 보수적으로 0.2 mm, 0.5mm를 선정하였다.(14) 전산유체역학 해석을 통해 예측된 파울링 상황의 압력 증배 계수는 Fig. 12와 같다. 해석결과, 유동 튜브 주위에 0.2mm, 0.5mm의 표면 거칠기를 사용하여 파울링 영향을 반영한 두 해석은 전 레이놀즈수 영역에서 동일한 값을 가졌으며 파울링 영향이 없는 앞선 두 해석과도 동일한 값을 보였다. 파울링 영향을 고려하지 않은 해석과 파울링 영향을 고려한 해석의 오차를 Fig. 13에 나타내었다. 파울링 영향이 없는 조건에서 예측된 압력 증배 계수와 파울링 영향이 고려된 조건에서 예측된 압력 증배 계수의 최대 오차는 ±0.1% 이내로 평가되었다. Fig. 12 및 Fig. 13에서와 같이 유동 튜브 주위의 표면 거칠기 상태에 무관하게 동일한 압력 증배 계수를 가지는 것은 파울링 조건에서도 정확한 유량 측정이 가능함을 의미한다.
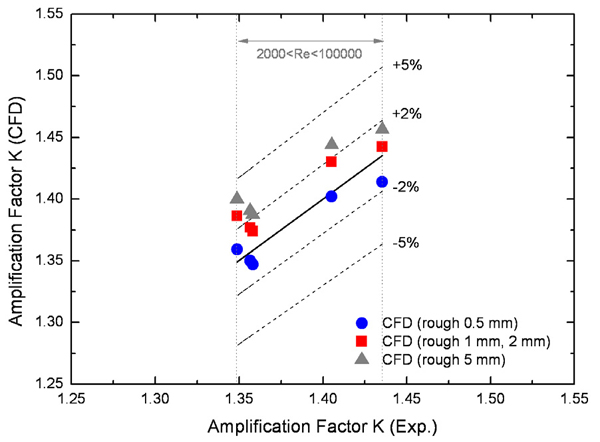
유동 튜브 주위의 표면 거칠기를 변경하며 평균 양방향 유동 튜브가 파울링에 무관한 유량측정이 가능함을 수치 해석적으로 증명하였다. 원자력 발전소 등 플랜트에서는 주기적인 정비를 수행하므로 표면 거칠기 0.5mm 이상의 파울링은 현실적으로 발생하지 않는다. 그러나 양방향 유동 튜브의 최대 허용 가능 파울링을 분석하기 위하여 BDFT 레이놀즈수 2,000 이상의 조건에서 유동 튜브 주위 벽면의 표면 거칠기를 1mm, 2mm, 5mm로 변경하며 추가적인 해석을 수행하였다. 난류모델은 SST 모델을 사용하였다. 해석결과, Fig. 14와 같이 표면 거칠기 1mm 및 2mm 조건에서는 압력 증배 계수가 동일한 값을 가지며 실험결과에 비하여 평균 1.5% 크게 예측하고 있다. 반면 표면 거칠기 5mm 조건에서는 평균 2.5% 크게 예측하고 있다. 이는 비록 현실적으로 불가능하기는 하지만 극도의 표면 거칠기를 유발하는 파울링 조건에서는 양방향 유동 튜브도 벤투리 유량계와 동일하게 실제 유량보다 큰 유량을 지시할 수 있음을 의미한다.
5. 결 론
3차원 전산유체역학 해석을 이용하여 Yun et al.이 개발한 평균 양방향 유동 튜브의 특성 및 압력 증배 계수에 대하여 평가하였다. 해석결과, 표준 k-ε 모델 및 SST 모델을 사용한 해석은 유동 튜브 주위의 유동 및 실험을 통하여 계산된 압력 증배 계수를 잘 예측하였다. 상업용 배관은 재질에 따라 고유 표면 거칠기를 가지므로 실제 원자력 발전소 등의 상업 플랜트에 양방향 유동 튜브를 이용한 유량계를 적용하려면 이에 대한 영향성 평가가 필요하다. 매끄러운 벽면 조건에 대한 해석결과를 바탕으로 상업용 강 및 스테인리스강의 고유 표면 거칠기를 적용한 해석을 수행하였다. 예측된 압력 증배 계수는 매끄러운 벽면 조건과 거친 벽면 조건에서 동일한 값을 가지므로 Yun et al.이 개발한 유량계가 상업적으로 활용되기에 문제가 없다고 판단된다. 파울링 영향이 고려되지 않은 두 가지 조건의 전산유체역학 해석을 통하여 평균 양방향 유동 튜브의 특성 및 압력 증배 계수를 적절히 모의할 수 있음을 확인하였다. 평균 양방향 유동 튜브가 파울링에 의해 미세 입자 부유물이 압력 도관에 침전되는 상황에서도 정확한 유량 측정이 가능함을 수치 해석적으로 증명하기 위하여 유동 튜브 주위의 벽면 거칠기를 변경하며 해석을 수행하였다. 해석결과, 유동 튜브 주위 0.2mm 및 0.5mm의 표면 거칠기 조건에서 압력 증배 계수는 동일한 값을 보였으며 파울링 영향이 없는 조건에서 계산된 압력 증배 계수와도 동일한 값을 보였다. 이러한 해석결과는 평균 양방향 유동 튜브를 이용한 차압식 유량계가 파울링 조건에서도 정확한 유량 측정이 가능함을 보여주는 결과이다. 향후 주급수 배관과 같이 대구경 배관에서도 평균 양방향 유동 튜브가 파울링에 무관하게 정확한 유량 측정이 가능함을 실험 또는 해석적으로 보일 수 있다면 원자력 발전소에서 사용되는 기존의 벤투리 유량계를 대체하여 사용할 수 있을 것으로 판단된다.
Acknowledgments
이 논문은 부산대학교 자유과제 학술연구비(2년)에 의하여 연구되었음
References
- 이덕기, “유량계의 기술동향 및 활용사례”, 제어계측, (2004.).
- Regan, J., Augenstein, D., Rodriguez-Lopez, M., Del Toro, S., “Generation increases at cofrentes nuclear power plant based on accurate feedwater flow measurement”, 9th International Conference on Nuclear Engineering, France, (2001.).
- Yun, B. J., Euh, D. J., Kang, K. H., Song, C.-H., Baek, W. P., “Measurement of the two phase mass flow rate using an average bidirectional flow tube”, 3rd ISTP, Italy, (2004.).
- Yun, B. J., Euh, D. J., Kang, K. H., Song, C.-H., Baek, W. P., “New Method for the Measurement of Two-phase Flow Rate using Average Bi-directional Flow Tube”, KNS Spring Meeting, Korea, (2004.).
- 김현정, 박종필, “급격 확대 및 축소관의 압력손실계 수에 대한 전산유체역학의 예측성능평가”, 한국공업화학회, (2010), 21(3), p258-264.
-
Gan, G., Riffat, S. B., “Measurement and computional fluid dynamics diffuser pressure loss coefficient”, Appiled Energy, (1996), 54(2), p181-195.
[https://doi.org/10.1016/0306-2619(95)00078-X]

-
Gan, G., Riffat, S. B., “Pressure loss characteristics of orifice and perforated plates”, Experimental Thermal and Fluid Science, (1997), 14, p160-165.
[https://doi.org/10.1016/S0894-1777(96)00041-6]

-
Mccaffrey, B. J., HesKestad, G., “A robust bidirectional low velocity probe for flame and fire application”, Combustion and Flame, (1976), 26, p125-127.
[https://doi.org/10.1016/0010-2180(76)90062-6]

-
Liu, C. Y., Wong, Y. W., Chan, W. K., Gan, T. C., “Note on the robust bidirectional low velocity probe”, Experiments in Fluids, (1990), 9, p354-356.
[https://doi.org/10.1007/BF00188768]

- Moody, L.F., Princetion, M.J., “Friction factors for pipe flow”, Transaction of the ASME, (1944), 66, p671-684.
-
Colebrook, C.F., “Turbulent flow in pipes with particular reference to the transition between the smooth and rough pipe laws”, Journal of the Institute of Civil Engineers London, (1939), 11, p133-156.
[https://doi.org/10.1680/ijoti.1939.13150]

- CD-adapco, User Guide STAR-CCM+ Version 8.02, CD-adapco, UK, (2013.).
- Wilcox, D. C., “Turbulence modeling for CFD”, DCW Industries, Inc., California, USA, (2006.).
- Spraying System Co, SF pressure drop online-calculator: Roughness of pipes, (검색일 : 2013. 6.14) http://www.spray.com/calculators/Pressure_Drop_Calc/rauh.html, (2013.).