스플리터의 코드길이와 피치방향 위치가 천음속 원심압축기의 유동 특성에 미치는 영향에 대한 전산해석적 연구

1. 서 론

전세계적으로 에너지 수요가 증가함에 따라 플랜트의 수요가 증가하여, 플랜트의 핵심요소 중 하나인 압축기에 대한 수요 역시 증가하고 있다. 또한 천연가스와 셰일 가스 등 차세대 에너지원의 채굴, 액화, 운송 등에 사용되는 산업용 가스압축기의 수요가 계속해서 증가할 전망이다.⁽¹⁾ 원심압축기는 터보형 압축기의 한 종류로, 축류형에 비해 운전범위가 넓고 단당 압축비가 큰 특징이 있어 다양한 산업분야에서 사용되고 있다. 최근의 국내외 터보압축기 개발현황을 살펴보면 고효율화를 지향한 대용량화와 고압 응용 분야 증가에 따른 고압화의 경향을 보이고 있다.

원심압축기의 압력비를 높이기 위해서는 임펠러의 회전수를 높이는 방법을 고려할 수 있다. 하지만 회전수를 증가시키면 작동유체의 상대속도가 증가하게 되는데, 상대속도가 음속 이상까지 도달하게 되면 임펠러 선단에서 충격파가 발생하게 되어 추가적인 손실이 발생하게 된다. 이러한 추가 손실을 최소화하기 위해 스플리터를 사용하는 방안을 고려할 수 있다. 일반적으로 스플리터는 메인 블레이드와 형상은 동일하나 축방향 코드길이를 짧게 설계하여 메인 블레이드의 중간 피치(mid-pitch) 위치에 배치한다.

천음속 원심압축기의 유동특성을 파악하여 압력비 및 효율을 높이려는 연구들이 실험 및 전산해석을 통해 진행되었다. Ibaraki 등과 Marconcini 등은 LDV 측정법과 전산유체역학(CFD)을 이용하여 이중 스플리터가 장착된 천음속 원심압축기의 설계점에서의 와류구조, 엔트로피 분포 등의 유동특성을 분석하였고^(2-4), 같은 압축기 모델을 이용해 서지 부근과 초킹 부근의 운전점에서의 유동특성을 파악하였다^(5,6). Yamada 등^(7,8)과 Tomita 등⁽⁹⁾은 현절비(solidity)가 다른 두 개의 천음속 원심압축기에 대해 팁 누설 와류의 영향과 공력 성능을 비교 분석하였다. 또한 원심압축기 임펠러 메인 블레이드의 형상을 변경하여 성능을 향상시키려는 연구들이 진행되었다. Hildebrandt 등⁽¹⁰⁾은 서로 다른 두 개의 후향각 및 세 개의 출구 폭을 갖는 임펠러들에 대해 유동 및 성능을 비교 분석하였다. Bonaiuti 등⁽¹¹⁾은 축길이, 전연후향각(leading edge sweep angle) 등을 설계변수로 하여 원심압축기의 최적화를 수행하였다. Oh 등⁽¹²⁾은 임펠러의 기울임각(lean angle)이 압축기의 공력 성능에 미치는 영향에 대해 연구하였다.

본 연구에서는 기존의 메인블레이드의 형상변수가 아닌 스플리터의 코드길이와 피치방향 위치를 설계변수로 하여 원심압축기의 유동 및 성능에 미치는 영향을 분석하였다. 이를 위해 기준이 되는 천음속 원심압축기를 설계하고, 스플리터 코드길이가 다른 4종의 파생모델 및 피치방향 위치가 다른 2종의 파생모델을 추가로 설계하여 비교하였다.

2. 임펠러 모델 설계

본 연구에서 설계한 원심압축기는 입구 덕트, 개방형(Open shroud) 임펠러 및 베인리스 디퓨저(Vaneless diffuser)로 구성되어있다. 1차원 성능 예측을 통해 2차원 자오면 유동장을 설계하고, 3차원 설계를 진행하여 3차원 유동해석결과로 유동장과 성능을 분석하는 설계 과정을 반복하였다. 1차원 성능해석은 RCOM1DR ver. 1.3을 사용하였고, 2차원 및 3차원 설계는 상용 프로그램인 ANSYS CFX-Bladegen 14.5를 사용하였다. 최종적으로 설계된 임펠러는 설계유량이 0.89kg/s일 때, 압력비가 4.0이고 임펠러 효율이 91.6%이다. Table 1은 1차원 공력 설계를 통해 나온 형상 설계 결과를 나타낸 것이다.

Table 1

Specification of impeller

Table 2는 기본모델 및 파생모델에 대한 모델명 및 형상정보를 나타낸 것이다. 7개의 임펠러는 크게 3개의 설계인자로 정의된 스플리터를 장착하고 있다. 스플리터 코드길이는 허브와 슈라우드에서의 코드길이를 이용하여 정의하였다. 본 연구에서는, 허브와 슈라우드의 코드길이비가 동일한 일반적으로 사용되는 스플리터 2종(ESTL001, ESTL003)과 허브와 슈라우드의 코드길이비가 다른 스플리터 2종(ESTL004, ESTL005)을 사용하였다. 또한 스플리터의 코드길이는 같지만 피치방향 위치가 변경된 경우(ESTL006, ESTL007)의 영향을 비교하였다. 피치방향 위치는 메인 블레이드의 흡입면으로부터 인접한 메인 블레이드의 압력면 방향으로의 거리를 비율로 나타내었다. 기본모델은 ESTL002로 명명하였는데 허브 및 슈라우드에서의 스플리터 코드길이가 메인 블레이드의 75%만큼의 길이를 가지며 50%의 피치방향 위치에 놓여 있는 경우이다. 임펠러의 블레이드 수, 팁간극과 직경비는 모두 동일하다.

Table 2

Comparison of test impellers

3. 수치해석 방법

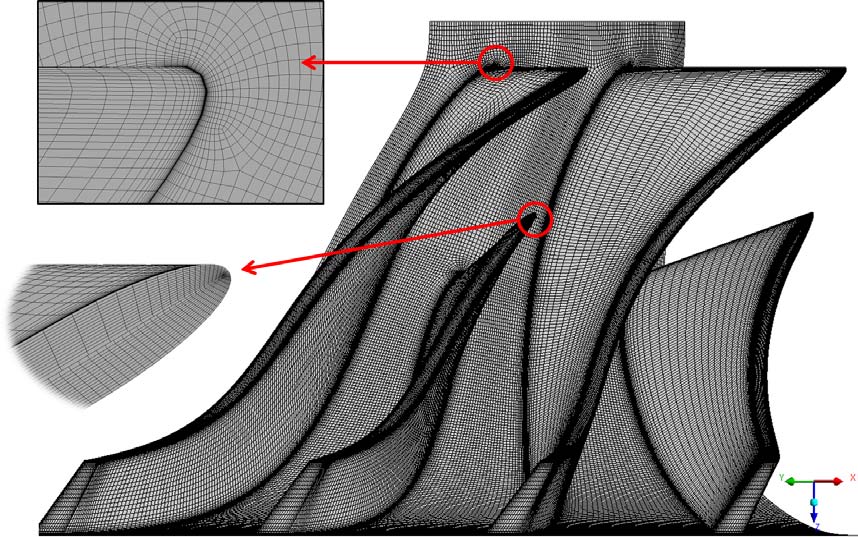
기본모델 및 파생모델에 대한 3차원 형상에 대해 ANSYS CFX-Turbogrid 14.5를 사용하여 격자를 생성하였다. 입구 덕트 약 10만 개, 임펠러 약 250만 개, 디퓨저 약 50만 개의 격자를 생성하고, y+는 2 이하의 값으로 설정하였다. 임펠러의 벽면근처의 격자 밀도를 높이기 위해 O형 격자를 이용하였으며, 익단간극에는 스팬 방향으로 10개의 격자수를 생성하여 익단 누설유동을 면밀히 관찰하고자 하였다. Fig. 1은 기본모델 임펠러의 격자 및 형상을 나타낸 것이다. 해석 시간을 고려하기 위해 주기조건(Periodic contidition)을 사용하여 메인 블레이드 및 스플리터가 각각 1개씩 포함된 영역을 대상으로 전산해석을 수행하였다. 정지계인 입구 덕트 및 디퓨저와 회전계인 임펠러 사이의 경계면은 Frozen rotor 기법을 사용하여 해석을 수행하였고, GGI(Generalized Grid Interface) 기법을 사용하여 각 영역간 경계면을 연결하였다. 점착조건(No-slip condition) 및 단열조건(Adiabatic condition)을 벽면에 주었으며, 난류모델은 역압력 구배 하에서 유동 박리의 시작과 그 크기를 가장 정확히 예측하는 것으로 알려져 있는 k-ω SST 모델을 사용하였다.⁽¹³⁾Table 3에 나타낸 바와 같이 해석영역의 입구에는 전압력과 전온도를, 출구에는 설계 유량을 각각 경계조건으로 주었다.

Fig. 1

Mesh of impeller, leading edge, and hub surface details

Table 3

Boundary conditions

4. 수치해석 결과 분석

4.1 스플리터의 허브와 슈라우드 코드길이비가 동일한 모델에 대한 분석

기본 모델인 ESTL002는 앞서 Table 2에서 나타낸 바와 같이 스플리터의 코드길이는 메인 블레이드의 75%이며 피치방향 위치는 50%이다. ESTL001과 ESTL003의 스플리터는 각각 메인 블레이드의 85%, 65%의 코드길이를 갖고 있다.

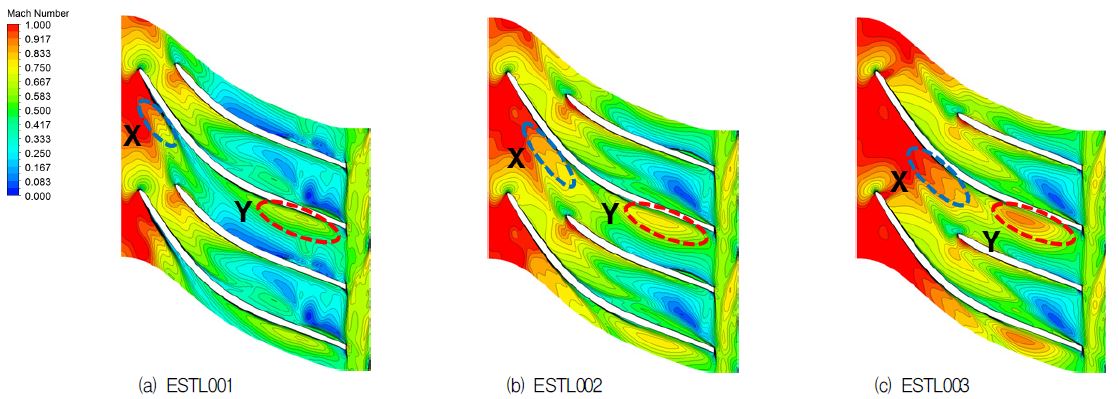
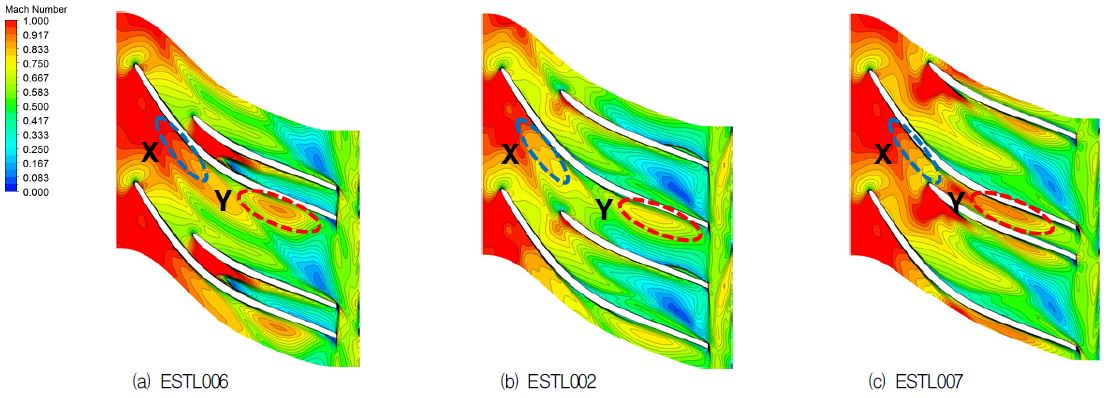
먼저 천음속 원심압축기의 유동특성을 비교하기 위해 팁 부근의 상대마하수를 비교하였다. 그 결과 Fig. 2에 나타낸 바와 같이 모든 모델에서 메인 블레이드의 흡입면 부근에서 충격파가 확인되었으며, 스플리터의 코드길이가 감소할수록 충격파의 발생 위치가 점차 하류로 이동하는 것을 X 영역을 통해 확인할 수 있다. 충격파에 의한 급격한 속도 구배는 정압 상승에 대한 손실을 유발한다.

Fig. 2

Relative Mach number distribution at 95% span

한편, 메인 블레이드의 흡입면과 스플리터의 압력면 사이의 통로인 Y 영역에서 상대 마하수가 증가하는 것을 볼 수 있는데, 스플리터의 코드길이가 감소할수록 속도 증가가 더 큰 것을 확인할 수 있었다. 유체의 운동에너지가 엔탈피 상승으로 이어지며 내부 압력이 증가하여야 하는데, 유로내의 속도 상승은 작동 유체에 가해진 운동에너지가 엔탈피 상승으로 이어지지 못하는 것을 의미하며 이는 곧 임펠러의 압력비가 감소하는 결과를 야기함을 의미한다. 실제로 속도 상승량이 가장 큰 ESTL003 모델의 압력비가 가장 낮게 나타났다(Fig. 8).

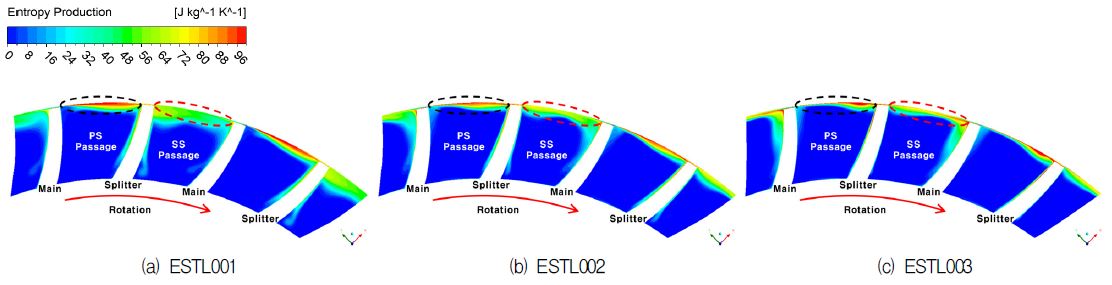
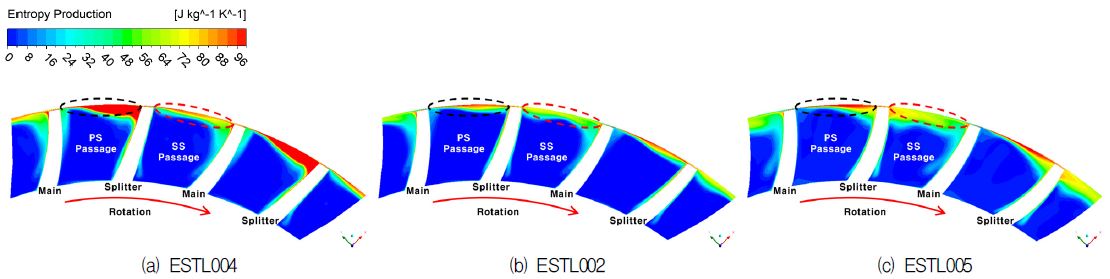
Fig. 3은 임펠러 축방향 코드길이의 50%에 위치하는 유로단면에서 유체의 운동에너지가 압력상승으로 전환되면서 발생되는 손실값을 입구 주유동에 대한 엔트로피 상승량으로 나타냈다. 엔트로피 상승량은 식 (1)을 이용하였다.

Fig. 3

Entropy distribution at mid-chord location

$\[ s-s_{\mathit{ref}}=C_p\ln \left(\frac{T}{T_{\mathit{ref}}}\right)-\overline{R}\mathit{ln}\left(\frac{P}{P_{\mathit{ref}}}\right) \]$

(1)

여기서 ref는 임펠러 입구를, $$ \overline{R}$$은 비기체 상수(Specific gas constant)를 의미한다. 또한 메인 블레이드의 압력면부터 스플리터의 흡입면 사이의 통로를 압력면 통로(Pressure side passage), 스플리터의 압력면부터 메인 블레이드의 흡입면 사이의 통로를 흡입면 통로(Suction side passage)라 명명하고, 손실영역을 압력면 통로와 흡입면 통로로 나누어 분석하였다.

그 결과 압력면 통로의 팁 근처 영역에서의 손실이 흡입면 통로보다 더 크게 나타났다. 이 영역은 메인블레이드로부터 발달한 익단 간극와류와 스플리터에 의한 익단 간극와류가 혼합되어 형성되는 구간이다. 흡입면 통로의 팁 근처 영역에서 발생하는 유동은 통로내부의 이차유동과 팁 간극와류의 혼합효과로 인해 발생한다. 모델별로 비교한 결과 스플리터의 코드길이가 감소할수록 압력면 통로에서의 손실의 크기가 감소하고 흡입면 통로에서의 손실 영역이 작아지는 것을 관찰할 수 있었으며, 이로 인해 스플리터 코드길이가 가장 짧은 ESTL003의 효율이 가장 높게 나타났다(Fig. 9).

4.2 스플리터의 허브와 슈라우드 코드길이비가 다른 모델에 대한 분석

일반적으로 원심압축기의 스플리터를 설계할 때 메인 블레이드의 전체 코드길이를 변화시키고 블레이드의 스팬 방향으로는 같은 비율을 적용한다. 최근에는 슈라우드와 허브의 코드길이가 다른 스플리터가 적용되고 있다. 앞서 Table 2에 나타낸 바와 같이 ESTL004 모델은 허브의 코드길이가 슈라우드의 코드길이보다 긴 스플리터를 장착한 임펠러이며 ESTL005 모델은 슈라우드의 코드길이가 허브의 코드길이보다 더 긴 스플리터를 장착한 임펠러이다.

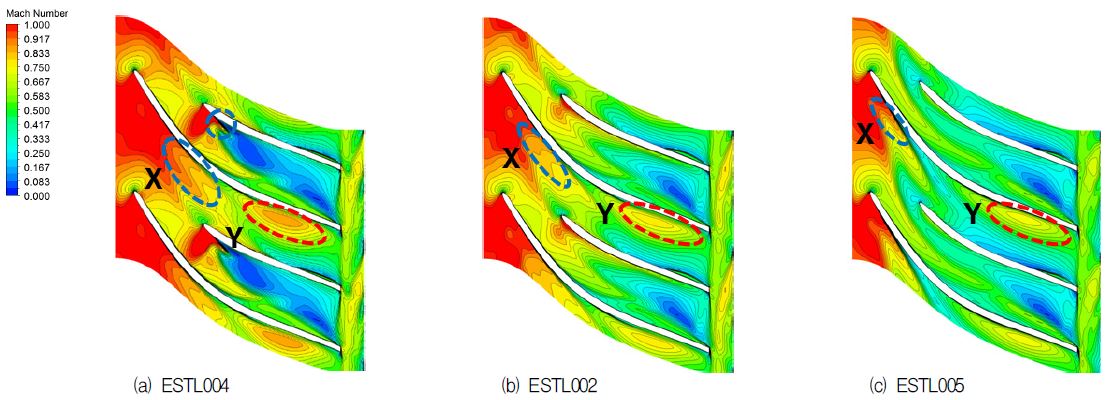
팁 부근의 마하수 분포를 확인한 결과 Fig. 4에 나타낸 바와 같이 메인 블레이드의 흡입면 부근에서 충격파가 관찰되며, 스플리터의 슈라우드 코드길이가 짧을수록 충격파의 발생 위치가 더 하류로 이동하는 것을 X 영역을 통해 확인할 수 있다. 따라서 Fig. 2와 Fig. 4의 결과를 봤을 때 스플리터의 슈라우드 코드길이가 충격파의 위치에 영향을 미친다는 것을 알 수 있다. 또한 Y 영역을 비교했을 때 ESTL004에서 유속 상승이 가장 크게 나타나는 것으로 보아 압력비에도 영향을 미친다는 것을 알 수 있다. ESTL004 모델의 경우 스플리터 선단 부근의 흡입면에서 추가적인 충격파가 발생하는 것을 볼 수 있는데, 이는 스플리터의 파손 위험을 증가시키고 압력비를 감소시킨다.

Fig. 4

Relative Mach number distribution at 95% span

Fig. 5는 임펠러 축방향 코드길이의 50%에 위치하는 유로단면에서 나타나는 손실값을 엔트로피 상승량으로 비교한 것이다. Fig. 3과 마찬가지로 압력면 통로의 팁 근처 영역에서의 손실이 흡입면 통로보다 크게 나타났다. 기본모델인 ESTL002와 비교했을 때 ESTL004는 압력면 통로에서의 손실의 크기가 크게 증가하고, ESTL005는 흡입면 통로에서의 손실 영역이 더 넓게 분포되어 효율이 감소하는 것을 알 수 있었다.

Fig. 5

Entropy distribution at mid-chord location

4.3 스플리터의 피치방향 위치가 다른 모델에 대한 분석

일반적인 원심압축기의 스플리터는 메인 블레이드의 손실영역을 감소시키기 위해 축소된 형태의 블레이드를 사용하며 대부분 메인 블레이드의 피치 가운데에 위치하도록 하고 있다. 하지만 Drtina 등⁽¹⁴⁾은 기존의 방법으로 설계한 스플리터 선단의 피치방향 위치를 메인 블레이드의 흡입면 방향으로 이동시킴으로써 날개 있는 디퓨저(vaned diffuser)에서의 압력 회복이 향상되었음을 확인하였다. 따라서 본 연구에서는 스플리터 전체의 피치방향 위치에 대한 특성을 관찰하고자 하였으며, 메인 블레이드의 피치를 사등분하여 압력면과 가까운 사등분 지점에 스플리터를 위치시킨 것을 ESTL006, 반대로 흡입면과 가까운 사등분 지점에 스플리터를 위치시킨 것을 ESTL007로 명명하였다.

Fig. 6은 팁 부근의 마하수 분포를 나타낸 것이며, 메인 블레이드의 흡입면 부근에서 충격파가 관찰된다. 스플리터의 피치방향 위치는 충격파의 위치에 큰 영향을 주지 않는다는 것을 알 수 있다. 그러나 ESTL006 모델의 경우 스플리터 선단 부근의 흡입면에서 충격파가 관찰되고, ESTL007 모델은 스플리터 선단 부근의 흡입면 및 압력면에서 충격파가 관찰된다. 또한 Y 영역에서 ESTL006과 ESTL007 모두 유속 상승량이 기본 모델인 ESTL002보다 높게 나타나 압력비에 영향을 미친다는 것을 알 수 있다.

Fig. 6

Relative Mach number distribution at 95% span

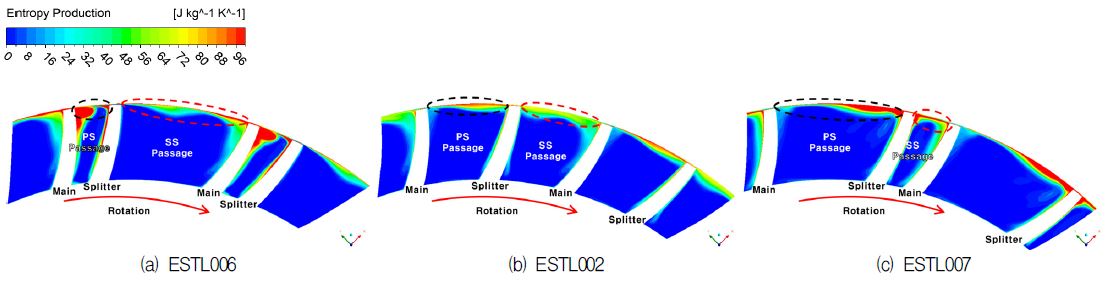
Fig. 7은 임펠러 축방향 코드길이의 50%에 위치하는 유로단면에서 나타나는 손실값을 엔트로피 발생량으로 비교한 것이다. 앞서 살펴본 Fig. 3과 Fig. 5와 마찬가지로 압력면 통로의 팁 근처 영역에서 손실이 가장 크게 나타났으며, 흡입면 통로의 메인 블레이드 팁 부근에서 손실이 가장 작게 나타났다.

Fig. 7

Entropy distribution at mid-chord location

4.4 임펠러 효율 및 압력비 비교

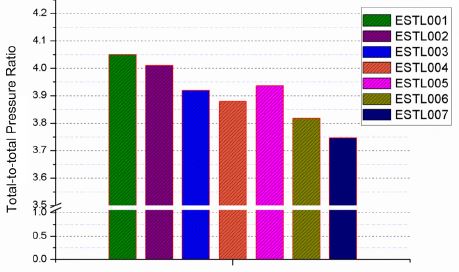
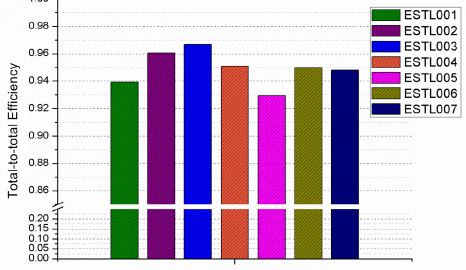
Fig. 8은 7가지 임펠러 모델의 total-to-total 압력비를 비교한 그래프이고, Fig. 9는 임펠러의 total-to-total 효율을 비교한 그래프이다. 임펠러 효율은 식 (2)와 같이 구할 수 있다.

Fig. 8

Comparison of pressure ratio

Fig. 9

Comparison of impeller efficiency

$\[ {\eta }_{\mathit{impeller}}=\frac{{\left(p_{02}/p_{01}\right)}^{\frac{k-1}{k}}-1}{\left(T_{02}/T_{01}\right)-1} \]$

(2)

앞에서 고찰한 속도장과 엔트로피 분포를 통해서 압력비와 효율이 변화되는 원인을 파악한 바 있다. 스플리터 코드길이가 감소할수록 압력비는 감소하고 효율은 증가하는 것을 확인할 수 있다. ESTL001는 기본 모델인 ESTL002에 비해 압력비가 약 1% 증가하였으나 효율이 약 2% 감소하였고, ESTL003은 압력비가 약 2% 감소하였으나 효율이 약 1% 증가하였다.

허브의 코드길이비가 슈라우드의 코드길이비보다 긴 ESTL004는 슈라우드의 코드길이비가 허브의 코드길이비보다 긴 ESTL005보다 압력비는 낮고 효율은 높게 나타났다. 또한 기본 모델인 ESTL002보다는 성능이 모두 낮게 나타났는데, ESTL004는 압력비와 효율이 각각 약 3%, 약 1% 감소하였으며 ESTL005는 약 2%, 약 3% 감소하였다.

피치방향 설치 위치와 관련하여, 스플리터가 메인 블레이드의 흡입면에 인접해 위치한 ESTL006이 압력면에 인접해 위치한 ESTL007보다 압력비와 효율 모두가 높게 나왔지만 기본모델보다는 성능이 낮게 나타났다. ESTL006은 기본 모델 ESTL002에 비해 압력비 약 5%, 효율 약 1% 감소하였고, ESTL007은 압력비 약 6.5%, 효율 약 1% 감소하였다. 스플리터의 압력면 통로와 흡입면 통로가 감소하면 충격파에 의한 손실 영역이 증대됨은 물론 엔트로피 상승량이 급격히 증가하기 때문에, 두 메인 블레이드의 중간 피치 위치에 스플리터가 위치해야 함을 확인하였다.

5. 결 론

본 연구에서는 스플리터의 코드길이 및 피치방향 위치가 천음속 원심압축기 성능에 미치는 영향을 살펴보기 위해 7가지의 임펠러 모델을 설계하였으며, 설계운전점에서의 성능 변화를 확인하였다. 그 결과를 요약하면 다음과 같다.

• 1) 스플리터의 코드길이가 짧아질수록 충격파의 위치가 하류로 이동하며, 압력비는 감소하지만 효율이 증가한다.
• 2) 스플리터의 허브 코드길이비와 슈라우드 코드길이비를 다르게 설계했을 때 슈라우드 코드길이비가 충격파의 위치와 압력비 및 효율에 영향을 미치고, 스플리터의 슈라우드 코드길이비가 짧아질수록 충격파의 위치가 하류로 이동하고, 압력비는 감소하며 효율이 증가하는 경향을 보인다.
• 3) 스플리터의 피치방향 위치가 메인 블레이드의 압력면에 인접한 것이 흡입면에 인접한 것보다 압력비와 효율이 높게 나타났으나, 기본 모델에 비해 성능이 모두 낮게 나타났다.

Acknowledgments

본 연구는 에너지기술평가원의 인력양성사업 (과제번호: 20144010200770) 및 한국연구재단의 일반연구자지원사업 (과제번호: 2013R1A1A2013701)의 지원을 받아 수행되었습니다.

References

• 권우성, (2012), “산업용압축기기술현황및발전”, 대한기계학회 기계저널, 52(10), p45-48.
• Ibaraki, S., Matsuo, T., Kuma, H., Sumida, K., and Suita, T., (2003), “Aerodynamics of a Transonic Centrifugal Compressor Impeller”, Journal of Turbomachinery, Vol. 125(No. 2), p346-351. [https://doi.org/10.1115/1.1540117]
• Ibaraki, S., Furukawa, M., Iwakiri, K., and Takahashi, K., (2007), “Vortical Flow Structure And Loss Generation Process In A Transonic Centrifugal Compressor Impeller”, Proceedings of ASME Turbo Expo, GT2007-27791. [https://doi.org/10.1115/gt2007-27791]
• Marconcini, M., Ibaraki, S., Rubechini, F., and Arnone, A., (2008), “Numerical Investigation of a Transonic Centrifugal Compressor”, Journal of Turbomachinery, Vol. 130(1), 011010. [https://doi.org/10.1115/1.2752186]
• Marconcini, M., Rubechini, F., Arnone, A., and Ibaraki, S., (2008), “Design and Off-design Numerical Investigation of a Transonic Double-Splitter Centrifugal Compressor”, Proceedings of ASME Turbo Expo, GT2008-50759. [https://doi.org/10.1115/gt2008-50759]
• Ibaraki, S., Sumida, K., and Suita, T., (2009), “Design and Off-design Flow Fields of a Transonic Centrifugal Compressor Impeller”, Proceedings of ASME Turbo Expo, GT2009-59986. [https://doi.org/10.1115/gt2009-59986]
• Yamada, K., Tamagawa, Y., Fukushima, H., Furukawa, M., Ibaraki, S., and Iwakiri, K., (2010), “Comparative Study on Tip Clearance Flow Fields in Two Types of Transonic Centrifugal Compressor Impeller with Splitter Blades”, Proceedings of ASME Turbo Expo, GT2010-23345. [https://doi.org/10.1115/gt2010-23345]
• Yamada, K., Furukawa, M., Fukushima, H., Ibaraki, S., and Tomita, I., (2011), “The Role of Tip Leakage vortex Breakdown in Flow Fields and Aerodynamic Characteristics of Transonic Centrifugal Compressor Impellers”, Proceedings of ASME Turbo Expo, GT2011-46253. [https://doi.org/10.1115/gt2011-46253]
• Tomita, I., Ibaraki, S., Furukawa, M., and Yamada, K., (2013), “The Effect of Tip Leakage Vortex for Operating Range Enhancement of Centrifugal Compressor”, Journal of Turbomachinery, Vol. 135, No. 5051020. [https://doi.org/10.1115/1.4007894]
• Hildebrandt, A., and Genrup, M., (2007), “Numerical Investigation of the Effect of Different Back Sweep Angle and Exducer Width on the Impeller Outlet Flow Pattern of a Centrifugal Compressor with Vaneless Diffuser”, Journal of Turbomachinery, Vol. 129(No. 2), p421-433. [https://doi.org/10.1115/1.2447873]
• Bonaiuti, D., and Zangenhe, M., (2009), “On the Coupling of Inverse Design and Optimization Techniques for the Multiobjective, Multipoint Design of Turbomachinery Blades”, Journal of Turbomachinery, Vol. 131, No. 2021014. [https://doi.org/10.1115/1.2950065]
• Oh, J. S., Buckley, C. W., and Agrawal, G. L., (2011), “Numerical Study on the Effects of Blade Lean on Highpressure Centrifugal Impeller Performance”, Proceedings of ASME Turbo Expo, GT2011-45383.
• Menter, F. R., (1992), “Improved Two Equation k-ω Turbulence Models for Aerodynamic Flows”, NASA Technical Memorandum.
• Drtina, P., Dalbert, P., Rüti, K., and Schachenmann, A., (1993), “Optimisation of a Diffuser with Splitter by Numerical Simulation”, ASME paper 93-GT-110.