피동 주입 시험 장치의 척도 해석 및 설계 방법론 연구

1. 서 론

세계 원자력 발전의 주요한 공급시장은 2000년대 이전에는 전력생산 목적의 대용량 발전로 중심으로 형성되어 왔으나, 이후에는 열병합, 해수담수화, 지역난방, 선박 추진 등 비발전 분야 활용에 적합한 중소형 원자로에 대한 잠재 수요가 증가하고 있다. 대형 원전 건설에 소요되는 막대한 초기 투자에 따른 재원 조달의 어려움, 투자 위험의 증가 등으로 상대적으로 건설 공기가 짧고 총사업비가 작아 다수의 소규모 수요에 맞춰 건설이 가능한 소형 모듈형 원자로 대한 관심이 증가하고 있다. 특히 후쿠시마 원전 사고 이후 원전의 안전성에 대한 대중의 관심이 증대되고 있으며, 국내 원전 산업의 경쟁력 제고를 위해 원전 사고 시 최소 3일 이상 동안 비상디젤발전기 작동이나 운전원조치 없이도 원전을 안전한 상태로 유도할 수 있는 피동안전계통을 갖춘 원전의 개발이 시급히 요구된다.

현재 개발도상국 및 선진국을 포함하여 15 개국 이상에서 45 종 이상의 중소형 원자로가 개발 중이며, 각국에서 개발을 추진 중인 중소형 원자로의 형태는 경수로, 중수로, 비등수로, 액금로 및 고온가스로 등으로 다양하다. 미국은 국제적인 경쟁 우위를 가지는 차세대 소형 모듈형 원자로의 개발을 활발히 추진하고 있으며, 현재 피동안전계통을 적용하여 개발을 추진하고 있는 대표적인 가압경수로 기반 중소형 원자로는 NuScale (Nuscale), mPower (B&W), 및 Westinghouse SMR (Westinghouse) 등이다. 미국 이외에도 일본(MRX, IMR), 러시아(VBER, KLT-40S), 중국(NHR200), 아르헨티나(CAREM) 등이 가압경수로 기반 중소형 원자로를 개발하고 있다.

피동안전계통의 설계 및 검증과 관련하여 미국에서 개발한 AP600⁽¹⁾ / AP1000⁽²⁾ 및 중국에서 개발한 CR600 / CR1000의 설계과정에서 피동안전계통의 검증을 위해 다양한 열수력 시험이 수행되었으나 공개된 자료는 극히 제한적이다. 국외에서 수행된 피동안전계통 관련 연구는 핀란드의 PACTEL 시험장치를 이용하여 수행한 노심보충탱크(CMT) 성능시험,^(3-5) 중국 NPIC에서 CMT Test Rig를 이용하여 수행한 CMT 성능시험,⁽⁶⁾ 일본 JAEA에서 수행한 ROSA/AP600 성능시험⁽⁷⁾ 등이 대표적이다. 또한 국내에서는 CP1300⁽⁸⁾의 피동안전주입계통으로 고려되었던 CMT의 거동에 대한 실험 및 해석연구^(9-11)가 비슷한 시기에 진행되었다.

한국원자력연구원은 2012년 7월 4일 국내 규제기관으로부터 SMART (System-integrated Modular Advanced ReacTor)⁽¹²⁾의 표준설계인가를 획득하고, 국내 건설 및 해외 수출을 추진 중이다. 가압기, 증기발생기, 원자로냉각재펌프, 원자로압력용기 등과 같은 주요 부품들이 대형 배관으로 연결된 일반적인 가압형 경수로와는 달리 일체형원자로인 SMART는 모든 주요 부품들이 하나의 압력 용기에 담겨 있다. SMART 표준설계는 상용 원전의 대형 배관에서 파단이 발생하는 대형냉각재상실사고 (LBLOCA, Large-Break Loss-Of-Coolant-Accident)를 근원적으로 배제하고 있다. 안전사고 관점에서 고려해야할 사고는 소형냉각재상실사고 (SBLOCA, Small-Break Loss-Of-Coolant-Accident)와 증기배관파단사고 (MSLB, Main Steam Line Break) 정도이다. 단일 호기 열출력이 330 MW인 SMART는 모듈형으로 구성하여 열출력을 증가시킬 수 있으며, 전기 생산과 함께 해수 담수화 기술에 적용할 수 있는 장점을 가지고 있다. 후쿠시마 원전 사고로 인해 국내외적으로 원자력 안전성 향상에 대한 요구가 거세지고 있는 상황에서, 일체형원자로로서 최초로 표준설계인가를 받은 SMART에 피동안전계통을 도입함으로써 SMART의 안전계통을 단순화시키고 안전성을 더욱 향상시켜 수출 경쟁력 강화 및 국내 건설시 주민 수용성을 제고할 필요성이 대두되었다. 이에 따라 장시간 원자로를 안정된 상태로 유지시킬 수 있는 SMART 피동안전계통의 개발이 추진되었고, 2012년에 개념 설계안을 도출하였다. SMART 피동안전계통의 개념 선정 및 계통 설계가 먼저 이루어졌으며, 안전해석 및 고유 해석모델 개발을 통해 해석적으로 안전성을 확인하고, 다양한 검증시험을 통해 설계 및 성능검증을 완료하여 향후 SMART의 국내 건설 및 국외 중소형원전 시장의 선점에 기여할 수 있을 것으로 판단된다. 피동안전계통을 구비한 SMART를 조기에 개발함으로써 2050년까지 약 350조원 규모로 추정되는 세계 중소형 원자로 시장의 약 10%를 점유할 수 있을 것으로 기대된다.

SMART 피동안전계통⁽¹³⁾의 개념 설계안은 SMART 표준설계 시 적용되었던 피동잔열제거계통(PRHRS, Passive Residual Heat Removal System), 4 대의 노심보충탱크(CMT, Core Makeup Tank)와 4 대의 안전주입탱크(SIT, Safety Injection Tank)로 구성된 피동안전주입계통(PSIS, Passive Safety Injection System), 2 단 밸브로 구성되는 자동감압계통(ADS, Automatic Depressurization System), 열교환기를 활용한 피동원자로건물냉각계통(PCCS, Passive Containment Cooling System) 등으로 구성된다. SMART-ITL을 활용한 피동안전계통 시험은 피동잔열제거계통, 피동안전주입계통, 자동감압계통 등에 대한 시험을 목적으로 한다.

이 시험장치는 피동안전주입계통과 자동감압계통 전체 4 계열(CMT 4개, SIT 4개, ADS 2개)이 SMART-ITL (Integral Test Loop) 규모(1/1-높이, 1/49-부피)로 축소 모의하여 기 구축된 SMART-ITL 시험장치에 부착하여 피동안전계통의 안전주입 성능 등을 종합적으로 검증하기 위해 설계되어 구축되었다. 본 논문은 SMART 피동안전계통 시험 장치의 설계 방법론을 소개하고, 이 방법론으로 구축된 개별 보충탱크의 주입 특성 시험을 상온/상압에서 수행하여 그 결과를 설계값과 비교하여 설계 방법론의 적합성을 평가하는 것을 목적으로 한다.

2. 시험 장치 설계 방법

3. 지배 방정식과 척도 해석

3.1 지배 방정식

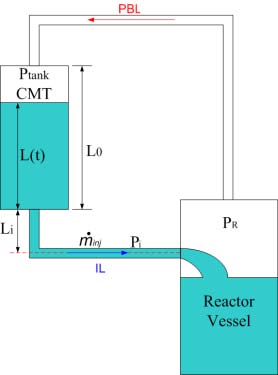
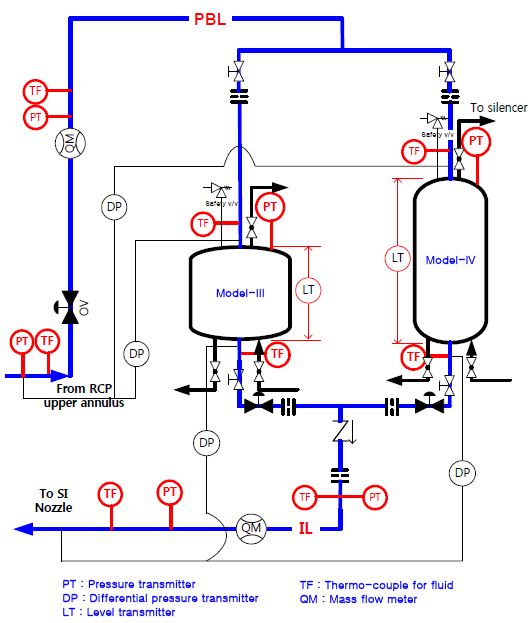
Fig. 1에 피동안전주입계통의 개념도를 간략하게 나타내었다. 주입탱크에 담긴 물이 중력 수두에 의해 주입되는 방식이기 때문에 지배방정식은 연속 방정식, 에너지 보존 방정식과 Darcy의 공식을 적용할 수 있다.^(14-17) 에너지 보존 방정식은 베르누이 방정식으로 간단히 정리될 수 있다.

Fig. 1

Schematic diagram of passive safety injection systemK : 주입 배관 형상 유로저항계수

$\[ \mathrm{Continuity\; Equation}:{\rho }_L{A}_{\mathit{Tank}}\frac{\mathit{dL}}{\mathit{dt}}=-{\stackrel{\text{̇}}{m}}_{\mathit{inj}} \]$

(1)

$\[ \mathrm{Darcy\; Formula}:h_i=\frac{{\upsilon }_i^2}{2g}{\left(\frac{\mathit{fl}}{d}+K\right)}_i=\frac{{\upsilon }_i^2}{2g}{\Pi }_i \]$

(2)

$\[ \mathrm{Bernoulli\; Equation}:\frac{P_T}{{\rho }_{L}g}+z_T+\frac{{\upsilon }_T^2}{2g}=\frac{P_i}{{\rho }_{L}g}+z_i+\frac{{\upsilon }_i^2}{2g}+h_i \]$

(3)

여기서 $$ {\Pi }_i=\left(f\frac{l}{d}+K_i\right)$$ : 유로저항계수

ρ_L : 냉각수 밀도
A_Tank : 탱크 단면적
L : 탱크에 담긴 냉각수 수위
L₀ : 탱크 수직 길이
L_i : 주입 배관 수직 높이
$$ {\stackrel{\text{̇}}{m}}_{\mathit{inj}}$$ : 주입 유량
P_T : 탱크 압력
P_i : 주입 배관 압력
v_i : 주입 배관 유속

주입 시점에서 보충탱크와 원자로냉각재계통의 상부는 압력평형배관으로 연결된 상태이기 때문에 P_T=P_i 이고, 초기의 탱크 수위의 하강 속도는 v_T =0이고, 보충탱크 수위는 z_T=L(t )+L_i 이며, 주입 배관 높이는 z_i=0이다. 식 (2)를 식 (3)에 대입하여 주입 배관의 유속으로 정리하면, 식 (4)와 같고 이것으로 식 (5)와 같이 주입 배관의 유량을 구할 수 있다. 이 주입 유량을 식 (1)에 대입하고, 초기 조건을 t=0 일 때, L=L₀을 대입하여 적분하면 식 (6)과 같은 수위에 관한 식으로 정리된다. 식 (6)을 다시 식 (1)에 대입하여 주입 유량을 구하면 식 (7)과 같다.

$\[ {\upsilon }_i={\left(\frac{2g\left(L+L_i\right)}{1+{\Pi }_i}\right)}^{1/2} \]$

(4)

$\[ {\stackrel{\text{̇}}{m}}_{\mathit{inj}}={\rho }_L{A}_i{\upsilon }_i={\rho }_L{A}_i{\left(\frac{2g\left(L+L_i\right)}{1+{\Pi }_i}\right)}^{1/2} \]$

(5)

$\[ L={\left({\left(L_0+L_i\right)}^{1/2}-\frac{C}{2}t\right)}^2-L_i \]$

(6)

$\[ {\stackrel{\text{̇}}{m}}_{\mathit{inj}}={\mathit{\rho }}_{\mathit{L}}{\mathit{A}}_{\mathit{Tank}}\mathit{C}\left({\left(L_0+L_i\right)}^{1/2}-\frac{C}{2}t\right) \]$

(7)

여기서, $$ \mathit{C}=\frac{{\mathit{A}}_{\mathit{i}}}{{\mathit{A}}_{\mathit{Tank}}}{\left\{\frac{2\mathit{g}}{1+{\mathit{\Pi }}_{\mathit{i}}}\right\}}^{1/2}$$

A_i : 주입 배관 단면적

3.2 척도법

시험 장치는 기본적으로 체적 척도법⁽¹⁸⁾을 적용하여 설계하였고, Ishii의 3단계 척도법⁽¹⁹⁾을 적용할 수 있도록 척도 해석을 수행하였다.

체적 척도법⁽¹⁸⁾은 높이, 시간 그리고 속도가 보존되는 특징을 가지기 때문에 중력 효과와 시간 척도가 중요한 시험에 유용하다. 특히, 안전주입탱크의 수위가 보존되기 때문에 냉각재상실사고 시험을 위한 장치에 적용하기 용이하다. 하지만, 원형과 시험 장치 사이의 종횡비(aspect ratio, 길이 대 직경 비)가 작아지게 되어 다차원 열수력 현상이 중요한 시험에는 적합하지 않다.

3단계 척도법⁽¹⁹⁾은 거시적 척도 단계, 각계통의 경계면에서의 질량 및 에너지 출입 보존을 위한 단계, 그리고 각 계통에서 발생 가능한 주요 국소 현상의 재현을 위한 국소 척도법 적용 단계로 구성된다. 이 방법을 적용하면 길이 축소가 가능하고 시험 장치의 종횡비를 원형에 가깝게 설계할 수 있게 되어 다차원 열수력 현상을 보존할 수 있다. 그러나, 길이가 짧아짐으로 인해 중력의 영향이 보존되지 않고, 시간과 유속이 보존되지 않아 국소적 열수력 현상이 왜곡될 여지가 있다^(20,21).

동일한 체적비를 가지면서 종횡비가 다른 탱크의 총 주입 시간이 동일해질 수 있다면 위의 두 가지 척도법이 가지는 장점을 유지하면서 단점을 보완할 수 있다. 즉, 길이가 보존되지 않는 모형에서 시간은 보존되면서 종횡비를 원형에 가깝게 제작하여 다차원 열수력 현상의 왜곡을 방지할 수 있다.

원형과 시험 장치에서의 체척비가 일정값으로 고정된 상태에서 종횡비가 서로 다른 피동형 주입 탱크가 중력 수두에 의해 동일한 주입유량분포와 총주입시간을 가지기 위해서는 탱크 설치 위치와 주입 배관의 유로저항계수에 대한 상사성 평가가 선행되어야 한다. 탱크 길이가 축소된 경우에는 탱크 길이 축소비만큼 주입 배관의 수직 높이도 축소하여 탱크를 설치하여야 하고, 유로저항계수는 주입 유량과 주입배관의 차압과 주입탱크의 수위 하강 속도에 대한 상사성을 유지함으로써 보존될 수 있다.

3.2.1 척도비 유도 방법

원형과 시험 장치에서 주입 시간을 보존하기 위해서는 주입 유량의 척도비가 체적비와 일치해야 한다. 주입 유량의 척도비는 식(8)과 같다.

$\[ {\stackrel{\text{̇}}{m}}_{\mathit{inj},\mathit{ratio}}={\left(\mathit{\rho \upsilon A}\right)}_{\mathit{ration}} \]$

(8)

주입 배관의 차압분포는 주입 탱크의 길이와 설치 위치에 의해 정해지기 때문에 차압의 척도비는 주입 탱크의 길이비와 일치한다. 차압 척도비는 식 (9)와 같다. 식 (4)를 식 (9)에 대입하면 식 (10)의 좌변과 같고, 식 (8)을 유속에 대해 정리하여 식 (9)에 대입하고 정리하면 식 (10)의 우변과 같아진다.

$\[ {\mathit{dP}}_{\mathit{ratio}}={\left(\mathit{\Pi \rho }{\upsilon }^2\right)}_{\mathit{ratio}}=L_{\mathit{ratio}} \]$

(9)

$\[ {\left({\Pi }_i\rho \left\{\frac{2g\left(L+L_E\right)}{1+{\Pi }_i}\right\}\right)}_{\mathit{ratio}}={\left({\Pi }_i\frac{{\stackrel{\text{̇}}{m}}_{\mathit{inj}}^2}{\rho A^2}\right)}_{\mathit{ratio}} \]$

(10)

중력 자체는 보존된다고 볼 수 있으므로 식(10)은 Π_i에 대해 식(11)과 같이 정리되어진다.

$\[ {\left(1+{\Pi }_i\right)}_{\mathit{ratio}}={\left(\left(L+L_E\right)\frac{{\rho }^2{A}^2}{{\stackrel{\text{̇}}{m}}_{\mathit{inj}}^2}\right)}_{\mathit{ratio}} \]$

(11)

만약 밀도가 보존되고, 원형에 대한 모델의 유로저항계수비가 Π_i,ratio=Π_i,M/Π_i,Pr 로 정의될 때, Π_i,M≫Π_i,Pr 이라면 주입배관의 유로저항계수 척도비는 식(12)와 같이 간략화할 수 있다. 여기서 Π_i,ratio는 모델과 시험장치에서의 주입배관 유로저항계수비이고, Π_i,M는 모델에서의 주입배관 유로저항계수이고, Π_i,Pr는 원형에서의 주입배관 유로저항계수이다.

$\[ {\Pi }_{\mathit{ratio}}=l_{\mathit{ratio}}{\left(\frac{A^2}{{\stackrel{\text{̇}}{m}}^2}\right)}_{\mathit{ratio}} \]$

(12)

체적비가 유지되면서 종횡비가 다른 주입탱크에 대한 척도비는 길이와 단면적 그리고 유량비에 관한 식으로 정리되고 이와 관련된 척도비는 Table 1과 같다. 여기서 아래 첨자 R은 ratio, M은 model(시험장치), Pr은 prototype(원형), T는 tank, Pi는 pipe를 뜻한다.

Table 1

Scale ratio of modeled tanks and pipes

3.2.2 척도비 적용 방법과 결과

척도법에 따라 시험 장치는 두 가지 형상으로 설계되었다. 동일한 체적비를 가지면서 수직 길이가 원형과 같은 것(model-I)과 원형의 1/2인 탱크(model-II)로 제작되었다. 탱크별 척도비는 Table 1과 같다. model-I과 II가 동일한 주입 시간을 가지기 위해서는 주입 배관의 유로 저항이 척도비를 만족해야 한다.

Table 1에서 주입 배관의 유로 저항비 Π_{R, Pi}는 탱크의 단면적비, 체적비, 그리고 수직 길이비와 상관관계를 가진다. model-I의 주입 배관이 탱크와 동일한 척도비를 가진다면, 단면적비와 체적비가 같고 수직 길이비는 보존되기 때문에 원형과 시험 장치에서의 유로저항계수는 동일할 것이다. model-II의 주입 배관이 탱크와 동일한 척도비를 가진다면, 원형과 시험 장치에서의 유로저항계수는 식 (12)에 의해 길이비와 면적비에 비례하고 주입유량비에 반비례할 것이다. 그러나 배관의 치수가 척도비에 의해 정해지더라도 정확한 치수의 상용 배관을 찾기 힘들고, 특히 본 시험 장치를 model-I, II와 같이 제작할 경우 서로 다른 직경의 주입 배관을 하나의 공통 배관으로 연결하여 원자로압력용기로 주입해야하기 때문에 각각의 독립적인 유로저항계수를 가지도록 주입 배관을 설계해야 하는 번거로운 단계를 거쳐야 한다.

그러나 만약 보충수탱크의 제원이 model-I, II와 각각 동일하고 주입 배관의 사이즈는 실제 척도에 의한 것보다 크지만 동일하게 선정할 수 있다면 실제 시험 장치의 제작에서 발생할 수 있는 번거로움을 제거할 수 있다.

본 시험 장치의 제작에 앞서 보충수탱크와 주입 배관의 척도비가 동일한 두 가지 모델(model-I과 II)과 서로 다른 두 가지 모델(model-III와 IV)에 대한 척도 해석을 통해 얻어진 각각의 유로저항계수를 이용하여 주입 유량을 평가하였다. model-III의 보충수탱크는 model-I과 동일하고 model-IV는 model-II와 보충수탱크는 동일하지만 주입 배관의 사이즈는 실제 척도에 의한 것보다 크게 선정하였고 model-III와 IV의 주입 배관 사이즈는 동일하게 선정하였다. Table 1에 주입 배관에 대한 척도 해석 결과를 나타내었다. Table 2에는 model-III의 설계 제원을 적용하여 시험 장치로 구성한 Case-I의 시험 결과로부터 얻어진 측정 초기값을 나타내었으며, 본 논문에서 이 값들은 무차원화를 위한 기준값으로 사용되었다.

Table 2

Scale ratio of modeled tanks and pipes

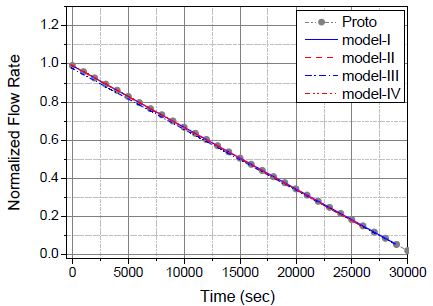
Fig. 2는 Table 1 의 척도 해석 결과를 주입 유량 식 (7)에 대입하여 구한 주입 유량 곡선이다. 보충수 탱크와 주입 배관의 기하학적 상사성이 유지되는 model-I과 II는 원형에서의 주입 유량에 척도비를 적용한 유량(Proto)과 정확하게 일치하는 유량 특성을 보여주고 있다. model-III와 IV는 장치 제작과 설치상의 이유로 주입 배관의 체적비가 정확히 보충수 탱크의 체적비를 만족하지 못하기 때문에 주입 초반 유량 차이가 존재하지만 전체적으로는 거의 동일한 주입 특성을 보여주고 있다.

Fig. 2

Flow rate of injection line

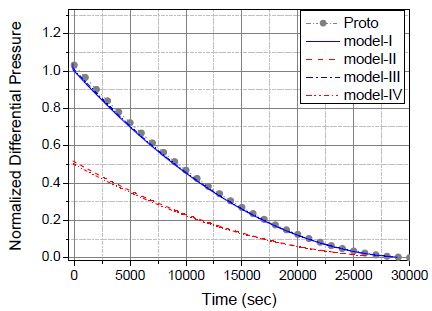
Fig. 3 은 주입 배관의 차압 분포를 나타낸 것이다. 주입 유량 식 (7)로 부터 주입 배관의 유속을 구하고, 유로저항계수 척도비로 부터 시험 장치 주입 배관의 유로저항계수를 구하여 관내 유동 차압(dP=Πρυ²/2)을 구한 결과이다. 주입 배관의 차압은 탱크 길이와 설치 위치에 따라 다른 분포를 보이고 있으며 차압의 최대값은 원형과 model-I, III가 model- II와 IV의 두 배이고 이것은 탱크 길이비와 동일하다.

Fig. 3

Differential pressure of injection line

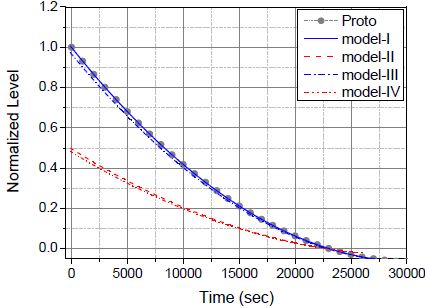
Fig. 4는 식 (6)을 이용하여 구한 주입탱크의 수위를 나타낸 것이다. 원형과 model-I, III의 수직 길이가 model-II와 IV의 2배임을 확인할 수 있다. 원형에서의 수위는 model-I과 II의 수위 분포와 거의 동일하고, 특히 model-I은 원형에서의 수위 분포와 완벽히 일치한다. model-II와 IV의 수위 분포 역시 거의 동일함을 확인할 수 있다.

Fig. 4

Water level of CMT

이론적인 설계값 평가를 통해 중력 수두에 의해 주입되는 피동주입탱크의 주입 유량은 배관의 유로저항계수 척도에 따라 원형의 주입 특성을 모사할 수 있음을 확인하였다.

4. 시험 방법 및 결과

4.1 시험 방법

실제 제작된 model-III와 IV를 이용하여 설계 요건을 만족하는지를 확인하는 검증 시험을 수행하였다. 시험에서 확인하고자 하는 바는 원형에 대해 동일한 체적비를 가지면서 서로 다른 수직 길이와 직경을 가지는 탱크의 보충수가 중력 수두에 의해 주입 배관으로 주입될 때 주입 유량 분포와 총 주입 시간이 설계 요건을 만족하는지를 확인하여 본 논문에서 제시한 설계 방법론을 검증하는 것이다.

앞서 언급했듯이 model-III와 IV의 주입 배관 체적비는 model-I, II와 동일하지만 단면적비는 체적비보다 크게 하여 주입배관의 길이는 줄어드는 방식으로 설계되었다. 이것은 배관에서의 마찰 저항이 model-I, II에서 보다 작아지게 설계하여 배관에서의 유로저항이 원형에서보다 작게 발생하도록 한 것이다. 시험 장치 주입 배관에서 척도에 의한 유로저항계수가 발생하기 위해서는 적절한 크기의 오리피스 설치가 필요하다. 본 시험은 오리피스 선정 시험을 선행한 후에 수행되었다.

시험 장치의 구성은 Fig. 5에 나타내었다. 체적비가 동일하고 종횡비가 서로 다른 탱크 model-III와 IV는 상부와 하부를 서로 연결하는 압력평형배관과 주입배관으로 각각 구성된다. 개별 구간과 공통 구간에 온도, 압력, 차압, 유량을 측정할 수 있는 계측기들이 설치되고, 개별 탱크에도 압력, 수위, 온도를 측정할 수 있도록 계측기가 설치된다. 시험에 사용한 계측기들의 측정허용오차는 Table 3에 표기하였다. 열전대는 측정값 대비한 오차이고, 열전대를 제외한 계측기들은 최대 측정 범위(Full Scale)에 대한 오차이다.

Fig. 5

test facility layout for passive injection system

Table 3

Acceptable mesaurement error

개별 탱크에 보충수를 만수위로 채우고 상온/상압의 조건에서 주입배관에 설치된 밸브를 열어 주입이 시작되면, 개별 탱크의 수위와 주입배관의 유로저항계수에 따라 주입유량이 형성되면서 수위 하강이 시작된다. 시험은 탱크에 채워진 냉각수의 수위가 탱크 바닥에 도달하여 더 이상의 주입유량이 측정되지 않을 때까지 수행하고, 시간에 따른 주입유량 분포, 차압 분포, 수위 분포를 비교하여 탱크별 설계사양을 만족하는지를 평가한다.

4.2 시험 결과

4.2.1 동일한 체적비와 총 주입 시간

본 절의 내용은 Table 4의 Case-I과 II에 해당하는 시험 결과에 관한 것이다. 시험의 목적은 동일한 체적비를 가지면서 종횡비가 서로 다른 model-III와 IV의 총 주입 시간이 설계값을 만족하는지를 확인하는 것이다. 원형설계에 대한 체적비가 동일하므로 탱크에 담을 수 있는 보충수의 부피는 두 탱크에서 동일하다. 종횡비가 다르기 때문에 탱크의 길이와 설치 위치에 따라 수두압은 서로 다르고 주입배관의 주입 초기 차압 또한 수위에 따른 수두압에 비례해야 한다.

Table 4

Test matrix

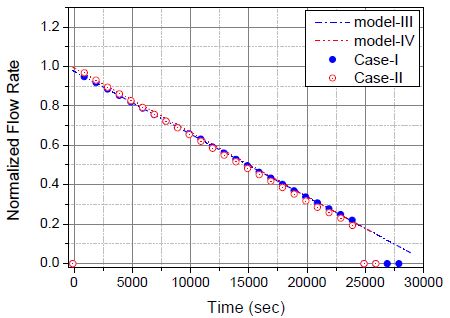
Fig. 6은 척도비를 적용한 원형 설계 주입 유량 분포와 주입 유량 이론식인 식 (7)에 유로저항계수비인 식 (12)를 적용하여 구한 설계 유량(점선, model-III와 IV)과 두 종류의 보충탱크 주입 유량 분포(원형, Case-I과 II)를 비교한 것이다. 주입 유량의 이론값은 식 (7)이 시간에 대한 선형방정식임을 정확하게 보여주고 있으며 시험 결과 역시 이와 거의 정확히 일치하고 있다.

Fig. 6

Comparison of injection flow rate between test and design value

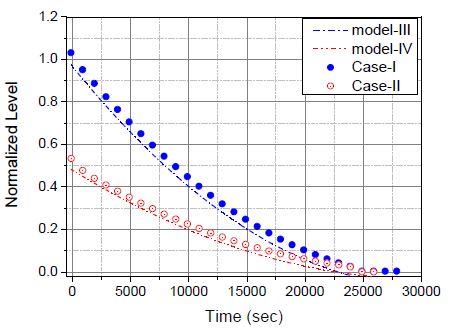
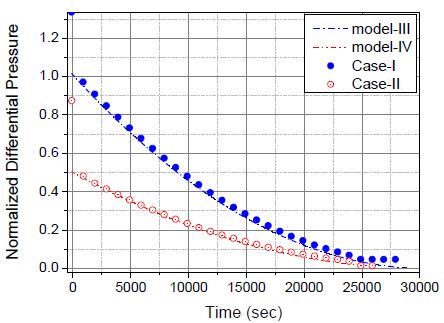
Fig. 7 과 8 은 보충탱크의 수위와 주입배관의 차압 시험 결과를 이론값(본문 3.2.2절 참조)과 비교한 것이다. 수위를 살펴보면, model-IV는 model-III의 절반 길이임을 알 수 있다. 차압 역시 주입 초기의 model-IV 값이 model-III의 절반임을 알 수 있다. 이것은 model-III의 절반 길이를 가지는 model-IV의 설치 위치가 model-III의 절반 위치라는 것을 반영한 것이다. 수위 하강 곡선과 주입배관의 차압 분포는 2차 함수 분포를 보이고 있다. 물리적 관점에서 주입배관에서 형성되는 차압은 중력 수두에 의한 주입유량의 종속변수로 주입유량의 제곱에 비례하므로 주입배관의 차압 분포는 정성적으로도 정량적으로도 합당한 분포를 보이고 있다. 이를 좀 더 살펴보면, 수위에 관한 식 (6) 역시 시간에 대한 2차 함수식으로 정의되고, 차압 분포 역시 식 (6)과 식 (9)을 참고하면 속도항은 수위에 비례하고 차압은 시간에 대한 2차 함수로 정의될 수 있음을 알 수 있다. 이론식과 시험 결과는 정량적으로나 정성적으로 잘 일치하고 있음을 확인하였다.

Fig. 7

Water level of model-III and IV

Fig. 8

Comparison of differential pressure between test and design value

중력 수두에 의해 주입되는 보충탱크가 동일한 부피를 가지면서 종횡비와 설치 위치가 서로 다르더라도 주입 유량 관점에서 동일한 주입 특성을 가질 수 있음을 확인하였다. 이것은 배관의 차압 특성을 결정짓는 유로저항계수의 선정 방법이 타당하였음을 보여주는 것으로 판단된다. 비록 짧은 길이를 갖는 보충탱크(model-IV)에 연결된 주입 배관에서의 차압 분포는 원형보다 낮은 분포를 보이지만, 피동형 주입 탱크의 목적은 주어진 부피의 보충수를 정해진 시간 동안 정해진 유량으로 주입하는 것이다. 서로 다른 높이의 탱크에 의한 차압 분포가 주입 특성 자체를 왜곡하지는 않기 때문에 차압 분포의 왜곡은 허용할 만하다고 볼 수 있다.

4.2.2 상사성 평가

시험 장치의 수력학적 상사성 평가는 Table 1과 같이 기본적인 설계 인자에 적용된 척도법의 적절성을 평가하는 기하학적 상사성 평가와 기본 설계 인자에서 유도되는 무차원변수의 보존 여부를 확인하는 동적 상사성 평가를 고려할 수 있다.⁽²²⁾

기하학적 상사성은 시험 장치에서의 유로형상이 원형과 동일하거나 일정한 축소비로 설계됨으로써 보존될 수 있다. Table 1에 나타낸 척도 해석 결과에서 확인할 수 있듯이 시험 장치에서 보충탱크와 주입 배관은 체적 척도법을 적용하여 동일한 척도비로 설계되었기 때문에 기하학적 상사성은 잘 유지되고 있다고 할 수 있다. 엄밀하게 말하면, model-I과 II는 정확하게 유지되고 있고, model-III와 IV의 주입 배관 척도는 체적비만 만족하기 때문에 정확하게 유지되고 있다고는 할 수 없으나 형상 측면에서는 유사성을 갖고 있다고 볼 수 있다.

동적 상사성은 압력, 유속, 밀도, 점성, 길이, 수력직경, 표면 거칠기와 같은 독립 변수로부터 유도할 수 있는 유로의 종횡비, 상대 거칠기, Euler 수, 그리고 Reynolds 수와 같은 무차원 변수로 평가할 수 있다. 특히, 원형과 시험 장치의 Euler 수와 Reynolds 수가 유사할 때 동적 상사성을 유지할 수 있다.

3.2절에서 언급한 바와 같이, 체적 척도법은 근본적으로 유로의 종횡비가 유지되지 않기 때문에 다차원 열수력 현상이 주를 이루는 시험 장치에는 적합하지 않은 방법이지만, 보충탱크 주입과 같이 중력 효과와 시간 척도가 중요한 시험에는 유용한 방법이다. 본 논문에서는 동일한 체적비를 가지면서 길이가 보존되는 보충탱크(model-I, III)와 길이가 원형의 1/2인 보충탱크(model-II, IV)를 설계하는 방법론을 제시하고 척도 해석을 수행하였다. 아울러 서로 다른 종횡비를 가지는 두 종류의 탱크 주입 특성은 주입 배관의 유로저항계수에 의해 결정됨을 보임으로써 길이가 보존되지 않는 변형된 체적 척도법의 타당성을 확인하였다. 다시 말해, 길이가 보존되지 않는 척도법을 적용하더라도 중력 수두에 의해 자연 주입되는 현상에서는 중력 효과와 시간이 보존되는 방법을 제시하였다고 볼 수 있다.

일반적으로 배관에서의 유로 저항은 마찰 저항과 형상 저항의 합으로 표현된다. 유로의 종횡비와 상대 거칠기는 마찰에 의한 유로 저항을 결정짓는 인자로 볼 수 있고, 배관의 곡관부, 밸브, 유량계 등은 형상 저항 인자로 볼 수 있다. 원형과 시험 장치에서 사용한 배관의 재질이 동일하다면, 표면 거칠기는 동일하지만 시험 장치에서는 기하학적 단면적이 축소되기 때문에 상대적인 거칠기는 축소비만큼 커지게 되고 결과적으로 마찰에 의한 유로저항을 증가시키게 된다. 이럴 경우에는 배관의 직경을 축소비보다 크게 하고 배관의 길이를 축소비보다 짧게 하여 상대 거칠기가 커지는 것을 완화시킬 수 있다. model-III와 IV가 이에 해당한다.

model-III와 IV에서 주입배관은 보충탱크와 같은 체적 척도비를 가지지만 면적비는 크게하고 배관의 길이는 짧게 하여 길이가 보존되는 체적 척도법에 의한 종횡비보다 작아지게 설계하였다. 이 방법을 적용하여 유로의 종횡비가 증가함으로써 발생할 수 있는 마찰에 의한 유로저항 증가 현상을 완화시켰다. 실제로 주입배관에서 발생하는 마찰에 의한 저항은 형상에 의한 저항에 비해 매우 작기 때문에 상사성 관점에서 상대 거칠기가 보존되지 않더라도 압력강하 관점에서의 주입 특성에 미치는 영향은 작다고 볼 수 있다. 특히 충분한 난류영역에서 마찰 저항의 영향은 더 작아진다.

형상 저항 인자를 포함하는 동적 상사성은 Euler 수로 평가할 수 있다. 식 (13)에서 확인할 수 있듯이 Euler 수는 유로 저항 계수를 대표하고 있으며, 마찰과 형상 저항 인자를 함께 내포하고 있다. Euler 수가 보존된다는 것은 시험장치에서의 유동조건이 원형에서와 같고, 기하학적 상사성이 유지된다는 것을 전제로 한다. 시험장치에서의 유동조건은 두 가지 관점에서 살펴볼 필요가 있다.

$\[ \mathit{Eu}=\frac{\mathit{dP}}{\rho {\upsilon }^2} \]$

(13)

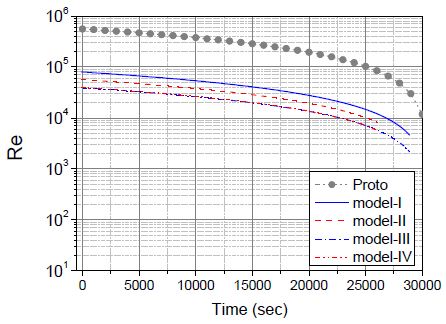
첫 번째는 Re 수의 보존이다. 기본적으로 시험 장치에서 유동조건이 원형에서와 같아지기 위해서는 Re 수가 보존되어야 한다. 만약 원형에서의 Re 수가 10,000 이상의 충분히 발달된 난류 영역이라면 시험장치에서의 Re 수도 충분히 발달된 난류 영역에 존재하기만 하면 된다. 원형과 시험장치의 유동조건이 충분히 발달된 난류 영역이라면 Re 수 차이에 의한 유로저항의 차이는 거의 없어지기 때문이다.

Fig. 9는 원형과 model-I에서 IV까지의 Re 수를 나타낸 그림이다. model-I과 II는 식(7)을 이용하여 구한 주입 유량을 유속으로 환산하여 구한 이론값이고, model-III와 IV는 Case-I과 II의 시험 결과로 얻어진 주입 유량을 유속으로 환산하여 구한 Re 수 분포이다. 원형에서의 Re 수는 10⁵ ~ 10⁶ 사이에 분포하고 있으며, 모델에서는 10⁴ ~ 10⁵ 사이에 분포하고 있다. 원형과 모델에서 Re 수가 차이가 나는 이유는 주입 유량의 척도비에 의한 것으로 볼 수 있다. 원형과 모델에서의 작동 유체는 물로 동일하고 주입 배관의 직경과 주입 속도는 척도비에 의해 결정된다. 즉, 물의 점성과 밀도는 원형과 모델에서 동일하고 주입 유속과 주입 배관의 직경은 척도비에 따라 줄어들기 때문에 Re 수 역시 원형에 비해 모델에서 작아진다. 초기 주입 유량을 기준으로 구한 원형에서의 Re 수는 5.6×10⁵이고, model-I에서는 8.0×10⁴이고, model-II에서는 5.6×10⁴이고, model-III, IV에서는 3.9×10⁵이다. 원형에서의 Re 수에 비해 모델에서의 Re 수가 Table 1에 나타낸 유속과 직경의 척도비 만큼 작아지고 있는 것이 이를 증명한다. 척도비에 의해 모델에서의 Re 수가 원형에 비해 줄어들고 있지만 주입 초기의 Re 수는 네 가지 모델 모두 10⁴ 이상의 완전 발달된 난류 유동 영역에 존재하고 있다. 비록 주입이 종료되는 단계에서 주입유량이 급격히 감소하면서 Re 수도 10⁴ 이하로 감소하였으나, 시험은 대부분의 영역에서 충분히 발달된 난류유동으로 진행되었음을 확인할 수 있다. 두 번째는 주입 배관에서의 압력 강하와 주입 유량 분포이다. 피동안전주입계통에서의 주입 배관 압력 강하 분포를 지배하는 인자는 중력 수두이고 초기 주입 유량과 주입 시간을 결정짓는 인자는 주입 배관에서의 유로저항계수이다. 중력 수두는 보충탱크의 수직 길이와 설치 높이에 따라 정해지고, 주입 배관에서의 유로저항계수는 배관의 종횡비 혹은 형상 인자에 의해 조절 가능함을 본문에서 확인하였다.

Fig. 9

Reynolds number for the test case

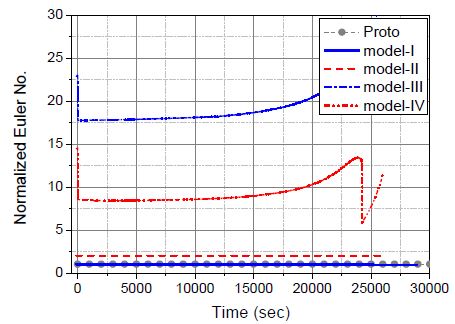
Fig. 10은 원형과 모델에서의 Eu 수를 원형에서의 Eu 수로 무차원화하여 나타내었다. 원형과 model-I에서의 Eu 수는 거의 완벽하게 일치하고 있으며, model-II는 원형보다 2배 크고, model-III는 원형보다 약 16.5배 크고, model-IV는 원형보다 약 8.25배 크다. 이것은 Table 1에 나타낸 주입배관의 유로저항계수 비(Π_{R, Pi})와 잘 일치한다.

Fig. 10

Normalized Euler number

즉, model-III와 IV는 탱크의 종횡비만 다를 뿐 체적 척도비는 동일하기 때문에 기하학적 상사성은 유지된다고 볼 수 있다. 그러나 주입 배관에서의 압력 강하 분포 등은 보충 탱크의 수직 길이와 설치 위치에 따라 달라지기 때문에 두 종류의 주입 배관에서 유로저항계수의 조절 없이 동일한 유동조건을 가지는 것은 현실적으로 불가능하다. 다시 말해, 유로저항계수의 조절로 인해 Eu 수는 보존되지 않지만, 대신 주입 유량 특성은 보존될 수 있다는 것을 뜻한다.

본 논문에서는 원형 설계와 시험 장치 설계에서 요구되는 최상위 요건인 초기 주입 유량과 주입 시간을 만족하는 유로저항계수를 선정할 수 있는 척도 해석 방법을 제시하였다. 척도법에 따라 제작된 보충탱크의 주입 시험 결과는 최상위 설계 요건을 만족함을 확인하였다. 이것은 설계 요건을 만족하는 시험 장치를 설계할 때 일반적으로 제시되고 있는 모든 상사성을 완벽하게 만족하지 않더라도 주요 상사성을 보존하는 것만으로 장치의 목적과 요건을 만족할 수 있음을 보여주었다.

즉, 유로저항계수를 조절함으로써 Eu 수는 보존할 수는 없고, 서로 다른 직경, 수직 길이, 그리고 설치 위치를 가지더라도 타당한 척도 해석 방법에 따라 설계된 시험 장치에서 수행한 시험결과는 동일한 주입 특성을 가질 수 있음을 확인하였다.

5. 결 론

피동형 안전주입계통의 성능 확인을 위한 시험 장치의 척도 해석과 설계 방법론에 관한 연구를 수행하였으며 결과를 요약하면 다음과 같다.

• 1) 체적비를 동일하게 유지하면서 서로 다른 종횡비를 가지는 피동형 안전주입탱크의 주입 시간과 주입 유량을 동일하게 유지할 수 있는 척도 해석을 수행하였다.
• 2) 척도 해석을 통해 원형과 모형에서의 주입 배관 유로저항계수비를 정량적으로 구할 수 있는 방법을 제시하였다.
• 3) 원형에 대한 모형의 체적비가 동일하고 종횡비가 다른 두 가지 탱크에 대한 주입 시험을 수행하였으며, 시간별 주입 유량 분포와 총 주입 시간이 일치함을 확인하였다.
• 4) 피동형 안전주입계통의 주입 특성은 탱크의 높이와 주입배관의 유로저항계수에 의해 주입 유량과 총 주입 시간이 결정됨을 확인하였고, 척도 해석을 통해 얻어진 원형과 모형에서의 유로저항계수비를 이용하면 총 주입 유량과 시간을 만족하는 시험 장치의 설계가 가능함을 확인하였다.

Acknowledgments

이 논문은 2016년도 정부(미래창조과학부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(SMART 고도화 공동개발사업, No. 2016M2C6A1004894).

References

• Tower, S. N., Schulz, T. L., and Vijuk, R. P., (1988), “Passive and Simplified System Features for the Advanced Westinghouse 600 MWe PWR”, Nuclear Engineering and Design, Vol. 109(No. 1), p147-154. [https://doi.org/10.1016/0029-5493(88)90153-7]
• Sutharshan, B., Mutyala, M., Vijuk, R. P., and Mishra, A., (2011), “The AP1000 Reactor: Passive Safety and Modular Design”, Energy Procedia, Vol. 7, p293-302. [https://doi.org/10.1016/j.egypro.2011.06.038]
• Tuunanen, J., Vihavainen, J., D, ’Auria, F., and Kimber, G., (1999), “Assessment of Passive Safety Injection Systems of ALWRs”, Final Report of the European Commission 4th Framework Programme Project FI4I-CT95-000 Technical Research Centre of Finland.
• Tuunanen, J., Riikonen, V., Kouhia, J., and Vihavainen, J., (1998), “Analyses of PACTEL Passive Safety Injection Experiments GDE-21 Through GDE-25”, Nuclear Engineering and Design, Vol. 180(No. 1), p67-91. [https://doi.org/10.1016/S0029-5493(97)00306-3]
• Vihavainen, J., and Tuunanen, J., (2002), “PACTEL Passive Safety Injection Experiments and APROS code Analysis”, Natural Circulation Data and Methods for Advanced Water Cooled Nuclear Power Plant Desings, IAEA-TECDOC-1281, Vienna, Austria, p183-194.
• Zejun, X., Wenbin, Z., Hua, Z, Bingde, C., Guifan, Z., and Dounan, J., (2003), “Experimental Research Progress on Passive Safety Systems of Chinese Advanced PWR”, Nuclear Engineering and Design, Vol. 225(No. 2), p305-313. [https://doi.org/10.1016/S0029-5493(03)00178-X]
• IAEA, (2012), “Summary on Natural Circulation Phenomena Observed in ROSA/AP600 Tests”, Natural Circulation Phenomea and Modeling for Advanced Water Cooled Reactors, IAEA-TECDOC-1677, Vienna, Austria, p286-298.
• Chang, S. H., No, H. C., and Baek, W. P., (1998), “Development of an Evolutionary Passive PWR Concept: CP-1300”, IAEA-SM-353/21P, p111-113.
• Lee, S. I., and No, H. C., (1998), “Gravity-driven Injection Experiments and Direct Contact Condensation Regime Map for Passive High-pressure Injection System”, Nuclear Engineering and Design, Vol. 183(No. 3), p213-234. [https://doi.org/10.1016/S0029-5493(98)00174-5]
• Lee, S. I., and No, H. C., (1997), “Assessment of RELAP5/MOD3.1 for Direct-contact Condensation in the Core Makeup Tank of the CARR Passive Reactor”, Annals of Nuclear Energy, Vol. 24(No. 7), p553-562. [https://doi.org/10.1016/S0306-4549(96)00086-2]
• Lee, S. I., and No, H. C., (1998), “Improvement of Direct Contact Condensation Model of RELAP5/MOD3.1 for Passive High-pressure Injection System”, Annals of Nuclear Energy, Vol. 25(No. 9), p677-688. [https://doi.org/10.1016/S0306-4549(97)00115-1]
• Kim, K. K., Lee, W. J., Choi, S., Kim, H. R., and Ha, J. J., (2014), “The First Licensed Advanced Integral Reactor”, Journal of Energy and Power Engineering, Vol. 8(No. 1), p94-102.
• Bae, Y., (2014), “System Description for Passive Safety Injection System of SMART”, SER-410-FS403-SD, KAERI, KOREA.
• Reyes, J. N. Jr, (2005), “AP600 and AP1000 Passive Safety System Design and Testing in APEX”, Natural circulation in water cooled nuclear power plants; Phenomena. Models, and Methodology for System Reliability Assessments, IAEA-TECDOC-1474, Vienna, Austria, p357-381.
• Shin, S. J., (2012), “Calculation of Hydraulic Resistance for Injection Line of Pressure Balanced Safety Injection Tank of SMART”, SER-410-FS301-004, KAERI, KOREA.
• Ryu, S., (2012), “Calculation of Hydraulic Resistance for Injection Line of Core Makeup Tank of SMART”, SER-410-FS301-002, KAERI, KOREA.
• Shin, S. J., (2012), “Performance Evaluation of Pressure Balanced Safety Injection Tank of SMART”, SER-410-FS301-013, KAERI, KOREA.
• Nahavandi, A. N., Castellana, F. S., and Moracdkhanian, E. N., (1979), “Scaling Law for Modeling Nuclear Reactor Systems”, Nuclear Science and Engineering, Vol. 72(No. 1), p75-83.
• Ishii, M., and Kataoka, I., (1983), “Similarity Analysis and Scaling Criteria for LWR’s Under Single-Phase and Two-Phase Natural Circulation”, NUREG/CR-3267, ANL-83-32, U. S. NRC, Washington, D. C.
• Yun, B. J., Kwon, T. S., Song, C. H., Euh, D. J., Chu, I. C., Park, J. K., Cho, H. K., and Park, G. C., (2000), “Development of Scaling Law for the Direct ECC Bypass during LBLOCA Reflood Phase with DVI Safety System”, Transactions of the Korean Nuclear Society Spring Meeting, KNS, KOREA.
• Yun, B. J., Park, C. K., Song, C. H., Kim, J. T., Kwon, T. S., Jun, H. K., and Cho, S., (1999), “Scientific Design of the Test Facility for the KNGR DVI Line Small Break LOCA”, KAERI/TR-1258/99, KAERI, KOREA.
• Euh, D. J., Yun, Y. J., Chu, I. C., Lee, J. W., Park, J. C., Kim, J. T., Bae, H., Park, C. K., Kwon, T. S., and Yi, S. J., (2010), “Test Facility for SMART Reactor Flow Distribution”, KAERI/TR-4239/2010, KAERI, KOREA.