윈드 쉬어에 의한 2 MW급 육상용 풍력터빈의 추력 특성 확인

1. 서 론

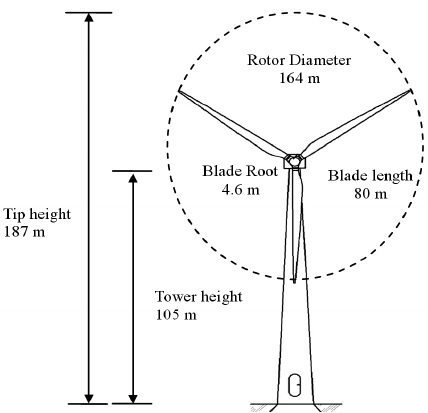
풍력터빈은 바람이 가진 에너지가 로터 블레이드를 회전시켜 기계적인 에너지를 전환하여 발전기를 통해 전기를 생산하는 기계이다. 최근 풍력터빈은 수 MW급으로 대형화되고 있고, 페더링 방향의 피치제어 방식인 가변속도-가변피치 형태를 취하고 있다. ^{(1, 2)} 풍력터빈 제작업체의 세계 1위 기업인 덴마크 Vestas 사는 다양한 MW급 대형 풍력터빈을 시장에 출시하고 있다. Vestas 사의 3MW급 육상용 모델인 V90은 블레이드 길이가 44미터이고, 3MW급 해상용 모델인 V112은 블레이드 길이가 54.65미터이고, 7MW급 해상용 모델인 V164는 블레이드 길이가 80미터이다( Fig. 1). ^{(3, 4)}

Fig. 1

Dimension of Vestas V164 7MW Wind Turbine (3. 4)

풍력터빈이 대형화됨에 따라 로터 블레이드가 회전할 때 블레이드에 발생하는 비대칭 하중이 증가하게 된다. 블레이드에 발생하는 비대칭 하중은 윈드 쉬어(wind shear), 타워 새도우(tower shadow), 난류(turbulence) 등에 의한 영향으로 주로 발생한다. ^{(5- 7)} 이들의 영향으로 풍력터빈 회전면에 불어오는 최대 풍속과 최소 풍속의 차이가 있고, 속도 차이에 의한 추력의 변동은 속도의 제곱에 비례하게 된다. 블레이드 길이 방향에서의 속도 차이에 의한 추력의 변동은 블레이드를 잡고 있는 로터 허브(hub)에 비대칭 모멘트를 주기적으로 일으키게 되고, 드라이버-트레인의 축과 베어링에도 동적 하중의 진폭의 증가를 야기하는 원인으로 작용한다.

IEC61400-1의 하중조건에서는 정적 극한 하중뿐만 아니라 동적 하중 조건도 규정하고 있는데, ⁽⁸⁾ 윈드 쉬어에 의한 동적 하중 변동도 그 중 하나의 경우가 된다. 이전 연구에서는 1MW급 풍력터빈을 대상으로 윈드 쉬어가 허브와 저속 전달축(LSS; low speed shaft)의 하중에 미치는 영향을 수치적으로 계산하였고, 이 동적 하중을 균일 흐름장에 놓였을 때의 하중 계산 치와 비교하였는데, 윈드 쉬어에 의한 동적하중은 무시할 수 없으며 반드시 풍력터빈의 설계 시에 고려해야 함을 보였다. ⁽⁹⁾

본 연구에서는 2 MW 풍력터빈을 대상으로 윈드 쉬어에 의한 추력의 변동을 상용 S/W인 Bladed를 이용하여 계산하여 풍속에 따른 추력 동적 하중의 변동 특성을 살펴보고자 한다.

2. 윈드 쉬어에 의한 추력

바람에 의해 발생하는 풍력터빈의 공력 토크는 식 (1)과 같이 표현되는데, 풍속뿐만 아니라 주속비와 피치각에 대하여 비선형적으로 표현된다.

여기서 ρ는 공기밀도, R은 로터의 회전 반경, β는 블레이드 피치각, V는 풍속, C _p는 출력계수, λ는 주속비이다.

이와 같이 바람에 의해 발생하는 풍력터빈의 추력은 식 (2)와 같이 표현되는데, 이 또한 풍속뿐만 아니라 주속비와 피치각에 대하여 비선형적으로 표현된다.

여기서 C _T는 추력계수이다.

블레이드가 세 개인 풍력터빈의 경우 식 (2)의 추력은 각 블레이드의 추력의 합으로 식 (3)과 같이 표현된다.

윈드 쉬어가 없는 경우 풍속은 블레이드 길이에 따라서 일정하지만, 윈드 쉬어가 있는 경우는 블레이드 길이에 따라 다르고 또한 로터의 회전각에 따라서 다르기 때문에 블레이드 각각에는 서로 다른 하중이 작용하게 된다. 윈드 쉬어는 지면으로부터 높아질수록 바람이 커지는데 식 (4)와 같다.

여기서 V _m은 로터 허브에서의 풍속, Z₀는 로터 허브 높이, h는 지면에서부터의 높이이고, α는 윈드 쉬어 지수값이다.

각 블레이드의 길이 방향에 대하여 임의 위치에서의 높이 h는 식 (5)와 같이 로터 회전각과 블레이드 길이의 함수로 표현된다.

여기서 블레이드 길이 방향의 거리 r의 범위는 0≤ r≤ R이고, θ는 로터의 회전 방위각(azimuth angle)이다.

윈드 쉬어 지수값 α는 지형에 따라서 다른 값을 가지는데, 본 논문에서는 육상용 풍력터빈을 대상으로 하고 있으므로, IEC61400-1의 하중조건을 따라 0.2의 값을 사용하여 계산한다.

3. 2MW 풍력터빈 모델

3.1 모델 파라미터

GL Garrad Hassan의 Bladed S/W에서는 2MW 풍력터빈 데모 모델을 제공하고 있다 ⁽¹⁰⁾. Bladed S/W에서는 블레이드, 로터, 타워, 파워 트레인 등 풍력터빈의 각 구성요소들을 표현할 수 있는 창들이 있는데, 거기에서 제시된 2MW 풍력터빈 데모 모델의 물리적인 파라미터값들을 정리하면 Table 1과 같다. 2MW 풍력터빈 데모 모델의 정격 파라미터값들은 Table 2와 같다. 정격풍속은 11.7 m/s이고 정격 발전기 속도는 1,500 rpm이고 정격 발전기 토크는 13.4 kNm이다.

Table 1

Physical parameter values for the 2MW wind turbine model

Table 2

Rated parameter values for the 2MW wind turbine model

3.2 토크 제어기

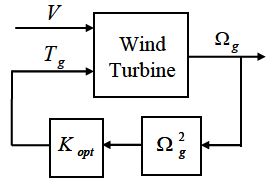
정격풍속 이하에서 풍력터빈의 제어는 토크 제어에 의해 수행되며, 이 경우 토크 제어의 목적은 최대의 출력파워를 생산하도록 하는 것이다. 이를 위해서는 주속비를 항상 최적값으로 유지하도록 해야 한다. 주속비의 최적값( λ _opt)은 출력계수가 최대값( C _p,max)이 될 때의 주속비 값이다. 최적모드게인을 이용하는 토크 제어 방법은 Fig. 2에서와 같이 풍속의 크기에 따라 최적 주속비( λ _opt)를 얻기 위하여 토크-속도의 정상상태 관계 특성을 나타내는 식 (6)을 이용하여 발전기의 토크크기( T _g)를 발전기의 회전속도( Ω _g)의 제곱에 비례하도록 제어하는 것으로 비선형제어 방법이다.

Fig. 2

Torque controller using optimal mode gain

$\[ T_g\left(t\right)=K_{\mathit{opt}}{\Omega }_g^2\left(t\right) \]$

(6)

여기서 K _opt는 최적모드게인으로 발전기의 토크와 발전기의 회전속도 사이의 이차 특성을 나타내는 계수값으로 식 (7)과 같다.

$\[ K_{\mathit{opt}}=\frac{1}{2{\lambda }_{\mathit{opt}}^3{N}_{\mathit{gb}}^3}\mathit{\rho \pi }{R}^5{C}_{p,\max } \]$

(7)

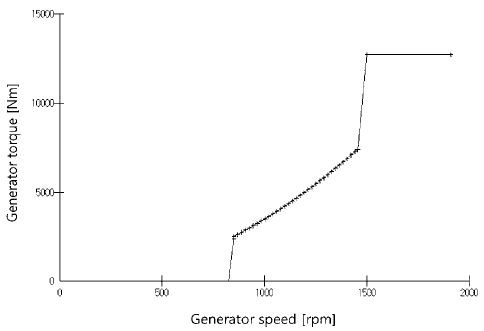
최적모드게인을 이용하는 토크 제어기는 천이 구간에서 급작스러운 토크 크기의 변화를 방지하기 위하여 토크 변화에 기울기를 주어 Fig. 3과 같이 최소 발전기 속도와 정격 발전기 속도 사이에서 순람표(look-up table)를 이용하여 실제 구현한다.

Fig. 3

A look-up table for the torque controller

3.3 피치 제어기

실제 풍력터빈 시스템에서는 드라이버-트레인(블레이드, 타워, 회전축 등)의 동적 특성이 나타나지만, 피치 제어기의 설계에 있어서는 기어박스의 증속비는 고려하나 드라이버-트레인의 강성과 감쇠를 무시한 1-질량 모델에 대하여 설계한다. 피치 제어기의 설계 시에 고려되지 않은 진동모드는 토크 제어기에서 드라이버-트레인 댐퍼를 통해 감쇠를 더해준다. 피치제어를 위한 되먹임 신호는 발전기의 회전속도를 사용한다. 피치 제어기는 발전기의 회전속도를 되먹임하여 기준입력인 발전기의 정격 회전속도와의 오차를 피치 PI 제어기를 통해 블레이드 피치각을 조절하는 방법이다. 피치 제어기는 공력 토크의 비선형성으로 인해 풍속의 크기에 따라 비선형적인 특성을 보인다. 그러므로 피치 PI 제어기는 게인-스케쥴링이 필수적이다. 피치 제어기( PC _sys( s))는 블레이드 피치각 조절을 위하여 비례게인( K _p)과 적분게인( K _i)으로 이루어진 피치 PI 제어기에 게인-스케쥴링(GS)을 적용한 형태로 식 (8)과 같다.

$\[ {\mathit{PC}}_{\mathit{sys}}\left(s\right)=\mathit{GS}\cdot C_P\left(s\right)=\mathit{GS}\left(K_p+\frac{K_i}{s}\right) \]$

(8)

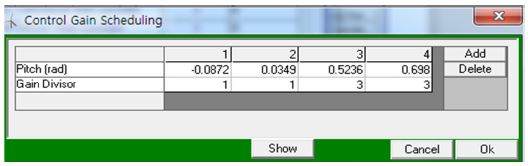
게인-스케쥴링은 피치각이 커짐에 따라 피치 PI 제어기의 게인값은 작아지도록 설계하였고, Bladed S/W에서 피치 PI 제어기의 게인-스케쥴링 설정은 Fig. 4와 같다.

Fig. 4

Parameter setting for pitch PI gain scheduling in Bladed

4. 2MW 풍력터빈 모델에 대한 추력 특성

4.1 윈드 쉬어가 없는 경우의 추력 특성

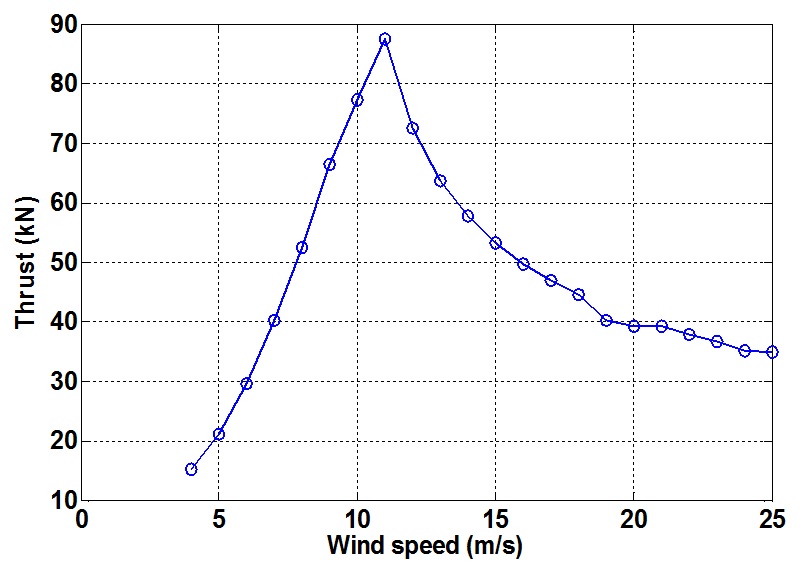
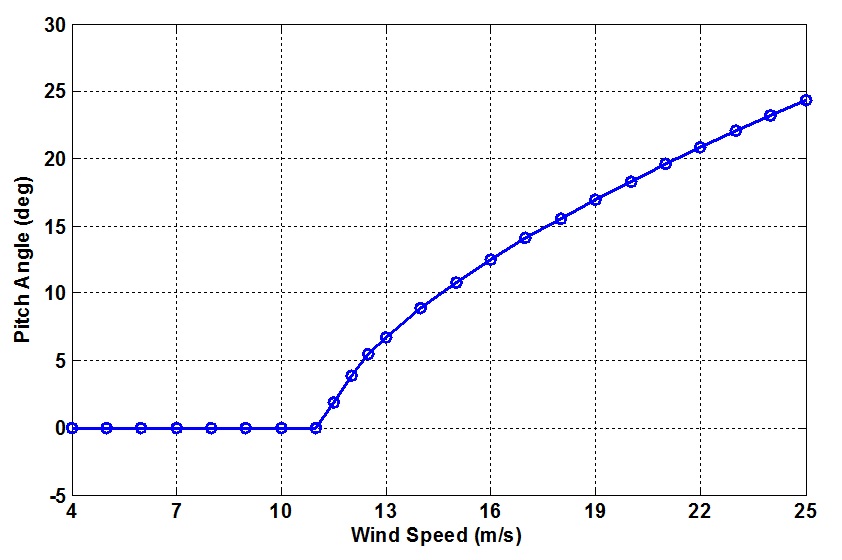
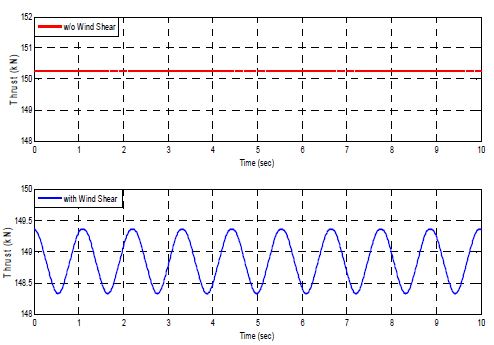
윈드 쉬어가 없는 경우 풍력터빈의 블레이드 세 개에 작용하는 추력은 모두 같고 각 블레이드의 추력이 합해져서 로터 허브에 추력을 발생시킨다. 앞에서 설명한 토크 제어기와 피치 제어기를 적용하여 로터 허브에서의 풍속( V _m)에 따른 각 블레이드에서 발생하는 추력의 크기와 로터 허브에서 발생하는 추력의 크기를 Bladed S/W를 이용하여 계산하였다. Fig. 5는 풍속에 따른 블레이드 하나에서 발생하는 추력의 정상상태 값을 보여주고 있다. 정격 이하의 풍속(4~11 m/s)에서는 피치각의 변화가 없으므로 풍속이 커짐에 따라 추력이 증가하는 것을 확인할 수 있다. 그러나 정격 이상의 풍속(12~25 m/s)에서는 풍속이 커짐에 따라 블레이드의 피치각이 증가함에 따라서 추력이 오히려 감소하는 것을 확인할 수 있다. 가변속도-가변피치 풍력터빈의 경우 추력은 정격 풍속 근처(약 8~16 m/s)에서 정적 특성의 영향이 가장 큼을 확인할 수 있다.

Fig. 5

Steady-state values of thrust on a blade according to wind speed without wind shear

Fig. 6

Steady-state values of pitch angle according to wind speed

4.2 윈드 쉬어가 있는 경우의 추력 특성

윈드 쉬어가 있는 경우 풍력터빈의 블레이드 세 개에 작용하는 추력은 모두 다르고 각 블레이드에서 발생하는 서로 다른 추력이 합해져서 로터 허브에 추력 변동을 발생시킨다. 로터가 회전할 때 각 블레이드에서 발생하는 추력은 로터의 회전 방위각에 따라서 변동하게 된다. 앞에서 설명한 토크 제어기와 피치 제어기를 적용하여 로터 허브에서의 풍속( V _m)에 따른 각 블레이드에서 발생하는 추력의 크기와 로터 허브에서 발생하는 추력의 크기를 Bladed S/W를 이용하여 계산하였다.

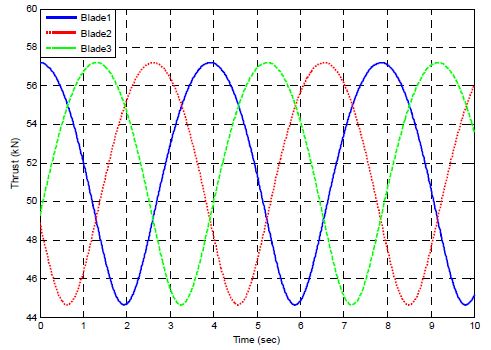
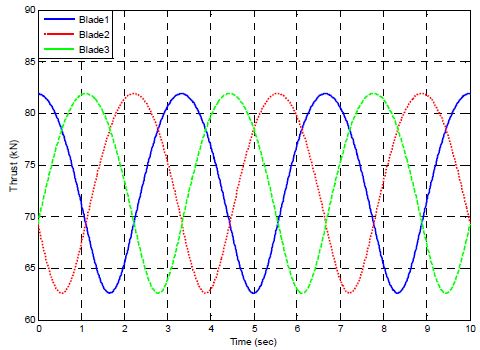
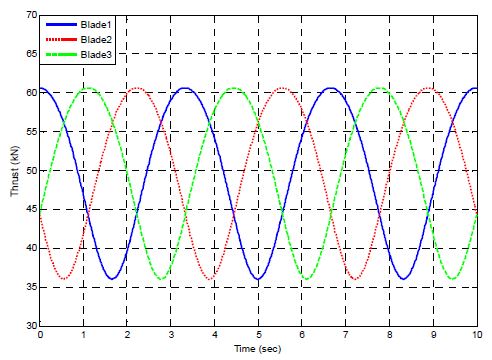
Fig. 7은 풍속 8 m/s에서, Fig. 8은 풍속 12 m/s에서, 그리고 Fig. 9는 풍속 16 m/s에서 각 블레이드에서 발생하는 추력을 보여주고 있다. 각 블레이드에서의 추력은 Fig. 5의 정상상태 값을 중심으로 시간에 따라 변동하는 것을 확인할 수 있다. 풍속이 증가할수록 각 블레이드에서의 추력 변동의 크기(피크-피크 값)는 커지는 것을 확인할 수 있는데, 풍속 8 m/s, 12 m/s, 16 m/s에서 추력 변동의 피크-피크 값은 각각 12.5 kN, 19.3 kN, 24.6 kN이다. 이는 정격풍속 이상에서 비록 피치각을 증가함으로 블레이드에 작용하는 추력의 정적 하중을 줄일 수는 있었지만, 윈드 쉬어에 의해 블레이드에 작용하는 추력의 동적 하중을 줄일 수는 없음을 말해 준다.

Fig. 7

Thrust variations on each blade at 8m/s under wind shear

Fig. 8

Thrust variations on each blade at 12m/s under wind shear

Fig. 9

Thrust variations on each blade at 16m/s under wind shear

각 블레이드에서 발생하는 추력의 변동은 로터 허브에 비대칭 하중으로 작용하여 로터 허브에 주기적인 동적 하중을 작용시키게 된다. Fig. 10은 풍속 16 m/s에서 로터 허브에 작용하는 추력의 동적 하중을 보여 주고 있다. 정격 로터속도는 18rpm이므로 각 블레이드에 0.3 Hz 성분(1P)을 발생시킨다( Fig. 8, Fig. 9). 그러나 로터 허브에서의 추력의 동적 하중은 세 블레이드의 비대칭 동하중이 합쳐진 것이므로, 각 블레이드에 작용하는 추력 동하중 주파수의 세 배 성분(3P)인 0.9 Hz가 가장 크게 나타남을 확인할 수 있다.

Fig. 10

Thrust variation at rotor hub at 16m/s under wind shear

5. 결 론

본 연구에서는 육상용 2 MW 풍력터빈을 대상으로 윈드 쉬어에 따른 블레이드 및 허브에 작용하는 추력의 특성을 상용 S/W인 Bladed를 이용하여 확인해 보았다.

윈드 쉬어가 없는 경우, 추력에 의한 정적 하중은 정격 이하의 풍속에서는 풍속이 증가함에 따라 커지고 정격 이상의 풍속에서는 블레이드 피치각이 커짐으로 인해 풍속이 증가함에 따라 오히려 작아지는 것을 확인하였다. 가변속도-가변피치 풍력터빈의 경우 추력에 의한 정적 하중은 정격 풍속 근처에서 그 영향이 큼을 확인하였다.

윈드 쉬어가 있는 경우, 각 블레이드에서는 추력의 변동에 의하여 비대칭 동적 하중이 발생하는데 추력 변동의 크기는 풍속이 증가할수록 커짐을 확인하였고, 블레이드에 작용하는 추력 동적 하중의 주파수는 로터 회전속도의 주파수와 같음을 확인하였다. 또한 각 블레이드에서의 추력의 변동은 로터 허브에 비대칭 하중으로 작용하여 로터 허브에 주기적인 동 하중을 작용시키게 됨을 확인하였고, 로터 허브에 작용하는 추력 동적 하중의 주파수는 로터 회전속도의 주파수의 세 배 성분이 가장 크게 영향을 미침을 확인하였다.

향후 본 연구결과를 바탕으로 윈드 쉬어에 의해 발생하는 추력의 동적 하중을 표현하는 모델을 풍력터빈용 상용 S/W인 Bladed와 동일한 결과를 보이도록 Matlab/Simulink를 통하여 구현하는 연구를 진행하고자 한다.

Acknowledgments

2015 한국유체기계학회 하계 학술대회 발표 논문, 2015년 6월 22~24일, 원주

이 논문은 2015년도 정부(교육부)의 재원으로 한국연구재단의 지원(NRF-2015R1D1A3A01019361) 및 한밭대학교의 지원(ERG)을 받아 수행된 연구입니다.

References

• Hansen, A. D., and Hansen, L. H., (2007), “Wind Turbine Concept Market Penetration over 10 Years (1995–2004)”, Wind Energy, Vol. 10(No. 1), p81-97. [https://doi.org/10.1002/we.210]
• Joselin Herberta, G. M., Iniyanb, S., Sreevalsanc, E., and Rajapandian, S., (2007), “A Review of Wind Energy Technologies”, Renewable and Sustainable Energy Reviews, Vol. 11(6), p1117-1145. [https://doi.org/10.1016/j.rser.2005.08.004]
• Vestas Website, www.vestas.com
• Ahmed, M. A., and Kim, Y, C., (2013), “Hybrid Communication Network Architectures for Monitoring Large-Scale Wind Turbine”, Journal of Electrical Engineering & Technology, Vol. 8(No. 6), p1626-1636. [https://doi.org/10.5370/JEET.2013.8.6.1626]
• Burton, T., Jenkins, N., Sharpe, D., and Bossanyi, E., (2011), “Wind Energy Handbook, Second Edition”, John Wiley & Sons, Ltd. [https://doi.org/10.1002/9781119992714]
• Manwell, J. F., Mcgowan, J. G., and Rogers, A. L., (2009), “Wind Energy Explained: Theory, Design and Application, Second Edition”, John Wiley & Sons, Ltd. [https://doi.org/10.1002/9781119994367]
• Bianchi, F. D., Battista, H. D., and Mantz, R. J., (2007), “Wind Turbine Control Systems: Principles, Modelling and Gain Scheduling Design”, Springer-Verlag. [https://doi.org/10.1007/1-84628-493-7]
• IEC61400-1, Third Edition, (2005), Wind Turbines-Part1: Design Requrements.
• Kim, J., Kang, S. H., and Ryu, K. W., (2016), “Comparison of Aerodynamic Loads for Horizontal Axis Wind Turbine (II): with and without Vertical Wind Shear Effect”, Journal of The Korean Society for Aeronautical and Space Sciences, Vol. 44(No. 5), p399-406. [https://doi.org/10.5139/JKSAS.2016.44.5.399]
• Bossanyi, E. A., (2009), GH Bladed Version 3.82 User Mamual.