진공청소기용 팬-모터 어셈블리의 시스템-레벨 분석
Abstract
A fan-motor assembly in a vacuum cleaner is analyzed through system-level analysis method. This system consisted of three components, a fan, motor, and the flow resistance of the motor, or of the vacuum cleaner. System-level analysis method is characterized by the combination of torque matching at a constant throttling condition between the fan and the motor and the pressure drop at a constant flow rate due to the flow resistance of the motor, or of the vacuum cleaner. The performance characteristics of the fan-motor assembly and the vacuum cleaner system could be predicted over the whole range of operation, based on the characteristics of each component. The predicted performance of the vacuum cleaner system through system-level analysis agreed well with the experimental results within 4.5% difference of pressure and 6% difference of the efficiency. The effect of flow resistance of a motor is investigated and it is found that the efficiency decrease of fan-motor assembly at the constant flow rate due to the flow resistance of a motor is determined by the flow resistance ratio(FRR), which is defined as a ratio of flow resistance of motor and the flow resistance of a constant throttling condition of a given point. The fan-motor assembly(S2 model) was modified to reduce the FRR from 9.0% to 2.4% and the experimental result shows that the efficiency of S2 model was improved by about 3% at best efficiency point.
Keywords:
System-level Analysis, Fan-motor, Flow Resistance, Torque Matching, Pressure Drop키워드:
시스템-레벨 분석, 팬-모터, 유동저항, 토크 매칭, 압력 강하1. 서 론
진공청소기는 전력소모가 큰 가전제품 중 하나이기 때문에 고효율의 진공청소기 개발은 에너지 절약 관점에서 매우 중요하다. 최근 EU의 Ecodesign과 Energy labeling에 대한 규정에서는 단계적으로 진공청소기의 최대 입력전력을 줄이고 (‘14년부터 1600 W 미만, ‘17년부터는 900 W 미만으로 제한) 에너지 효율을 제품에 명기하도록 하고 있다.(1,2) 또한, 사용자 편의를 위해 배터리를 사용하는 무선 청소기가 증가하는 추세인데, 이 역시 장시간의 배터리 사용을 위해서는 고효율의 진공청소기 개발이 필요하다. 고효율의 진공청소기 개발을 위해서는 진공청소기 내에서 흡입력을 발생시키는 고효율의 팬-모터 어셈블리의 개발이 필수적이다.
진공청소기 자체의 목표 스펙이 결정되면, 그에 맞는 팬-모터 어셈블리의 목표 스펙이 결정되고, 다시 팬과 모터 등의 개별 컴포넌트의 목표 스펙이 정해져서 개발이 이루어지게 된다. 이를 위해서는 개별 컴포넌트, 팬-모터 어셈블리 그리고 진공청소기 시스템 특성 간의 상호 관계를 이해하고, 설계 초기부터 시스템-레벨에서 설계를 진행하는 일은 우수한 성능의 진공청소기 모터 개발 및 개발기간 단축에 매우 중요하다. 개별 컴포넌트의 설계에서 우수한 성능의 팬 또는 모터를 개발하였다 할지라도, 컴포넌트 간의 매칭 특성이 좋지 않아 팬-모터 어셈블리나 어셈블리가 장착된 시스템의 성능이 원하는 스펙을 만족하지 못 하는 경우가 종종 발생한다. 이러한 경우 팬 또는 모터의 수정설계가 이루어 져야하는데 대부분은 경험에 의하거나 반복적인 테스트를 통해 이루어진다. 따라서 고효율의 진공청소기나 진공청소기용 모터 개발을 위해서는 개별 컴포넌트의 성능을 향상시키는 것외에, 이러한 상호관계를 고려하여 시스템-레벨에서 팬-모터 어셈블리나 진공청소기 시스템의 특성을 최적화 하는 것이 또 하나의 방법이 될 것이다.
팬의 특성과 모터의 특성을 같이 고려하여 팬-모터의 성능을 예측하려는 연구들이 있었는데, Epple(3) 등은 모터의 토크회전속도 특성을 고려한 평균유선법를 통하여 원심 임펠러의 유량에 따른 회전속도의 변화 및 그에 따른 성능 예측을 하였다. Herber와 Li(4)는 농업용 환기 팬의 성능 예측 및 이를 통한 팬과 모터의 적절한 조합을 찾기 위해, 모터의 성능특성과 임펠러의 특성을 결합하여 자유 송출조건에서의 팬-모터의 성능 예측을 하였다. Lin과 Tsai(5)는 실험으로부터 얻은 팬-모터의 특성과 전산유체역학 해석으로부터 얻은 팬의 특성으로부터 모터의 효율 및 성능특성을 추출하는 방식으로 팬과 모터의 성능을 예측하였다. Park(6) 등은 팬, 모터, 그리고 유동저항의 상호관계를 고려하여 전체 유량 영역에서 팬-모터 어셈블리와 이를 장착한 시스템의 특성을 예측하는 시스템-레벨 설계기술을 제안하고, 이를 위해 ACE(Air-moving Characteristics Estimation) 소프트웨어를 개발하였다. ACE를 통해 개별 컴포넌트 특성으로부터 팬모터 어셈블리나 진공청소기 시스템의 성능을 예측하고, 컴포넌트간의 상호관계를 고려하여 팬-모터 어셈블리의 성능을 최적화하는 방법에 대해 연구하였다.
본 연구에서는 ACE를 이용하여 실제 진공청소기 시스템의 성능 특성을 예측하고 이를 실험을 통하여 검증하였다. 또한, 모터의 유동저항이 팬-모터 어셈블리의 성능에 미치는 영향을 분석하고 모터의 유동저항을 감소시킨 모델에 대해 실험을 통해 효율 상승의 효과를 확인하였다.
2. 시스템 정의 및 성능 측정 방법
2.1 시스템 정의
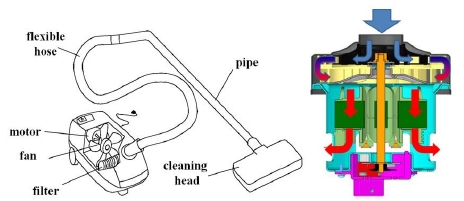
진공청소기에 사용되는 팬-모터 어셈블리는 흡입된 공기의 이동경로에 따라 bypass 타입과 through-flow 타입으로 나눌 수 있다.(1,7) Bypass 타입 모터에서는 팬을 지난 공기는 모터를 거치지 않고 바로 배출되는데, 이 때문에 모터의 냉각을 위해 별도의 냉각용 팬이 필요하다. 가정용 진공청소기에 널리 사용되는 through-flow 타입 모터의 경우 Fig. 1에 나타낸 바와 같이 팬을 지난 공기는 모터를 통과하며 냉각시킨 후 모터 하우징의 출구를 통해 배출된다.
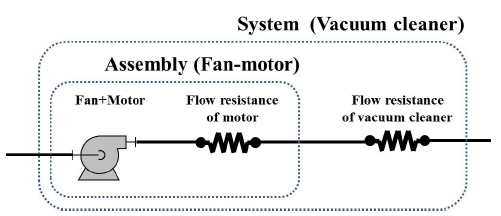
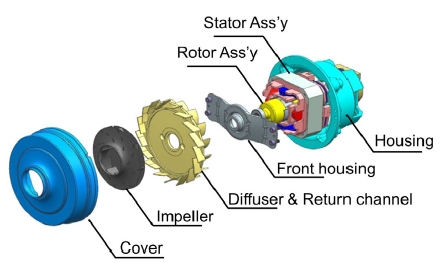
본 연구에서는 Fig. 2에 나타낸 바와 같이 편의상 팬과 모터 등 기본 컴포넌트의 조합으로 이루어지는 팬-모터를 어셈블리, 팬-모터 어셈블리가 장착된 진공청소기를 시스템이라고 부른다. 어셈블리는 팬, 모터 그리고 모터의 유동저항으로 정의하고, 시스템은 어셈블리에 진공청소기의 유동저항까지 포함한다. 어셈블리의 유동저항은 Fig. 1의 through-flow 타입 모터에서 팬을 지난 공기가 모터를 냉각하며 겪는 모터의 유동저항이다. 시스템의 유동저항은 Fig. 1에 나타난 대로, 내부에 장착된 팬-모터 어셈블리에 의해 흡입된 공기가 클리닝 헤드, 파이프, 필터 등의 진공청소기 내부 구조물을 거치며 겪는 유동저항을 의미한다. 본 연구에서는 청소기용 팬-모터 어셈블리로 Fig. 3의 S2 모델을 사용하였다. S2 모델은 슈라우드 2D 임펠러와 디퓨저, 그리고 리턴채널로 구성되고, 모터는 Switched Reluctance Motor(SRM)가 사용되었으며 약 39,000 rpm의 회전속도를 가진다.
2.2 성능 측정
팬-모터 어셈블리나 진공청소기 시스템의 성능은 흡입일률 시험기(suction power tester)로 측정되며 균압박스에 장착된 오리피스(orifice) 직경을 변경해가며 입력전력, 회전속도, 압력, 유량 등의 성능특성을 측정한다. 어셈블리나 시스템과 관련된 목표 스펙은 특정 오리피스 또는 특정 오리피스 구간에서 일정값 이상의 효율을 가지도록 설계하는 것이 일반적이다. 오리피스는 시스템 저항를 대변하는 등가 시스템으로 볼 수 있고 팬의 회전속도 변경에 의해 작동점은 바뀌지 않기 때문에 청소기용 팬-모터의 개발 시 오리피스 기준의 설계목표가 사용된다.
IEC 규격(8)에 의해 제작된 흡입일률시험기를 이용하여 청소기용 어셈블리의 성능이 측정되었다. 테스트 챔버는 내부 500 mm×500 mm×500 mm 크기의 균압박스가 이용되었다. 진공청소기의 성능 측정 시에는 클리닝 헤드를 제거하고 파이프를 흡입일률시험기에 직접 연결하여 측정하였고(Fig. 1 참조), 팬의 회전속도는 SRM 에 부착된 홀 센서(hall sensor) 신호로부터 계산하였다. 모터나 시스템의 유동저항 측정을 위해서는 ANSI/AMCA 210-99(9)에 의거하여 제작된 멀티-노즐챔버 타입의 팬 성능 시험장치(fan performance tester)를 사용하였다. 모터의 특성은 Magtrol社의 고속기기 시험용 다이나모미터(모델명: 2WB43-HS)를 이용하여 측정하였다.
3. System-level analysis 방법
3.1 Component level 특성
팬의 효율은 식 (1)과 같이 모터로부터 받는 축동력과 팬에 의해 유체로 전달되는 유체에너지의 비로 표현된다.
| (1) |
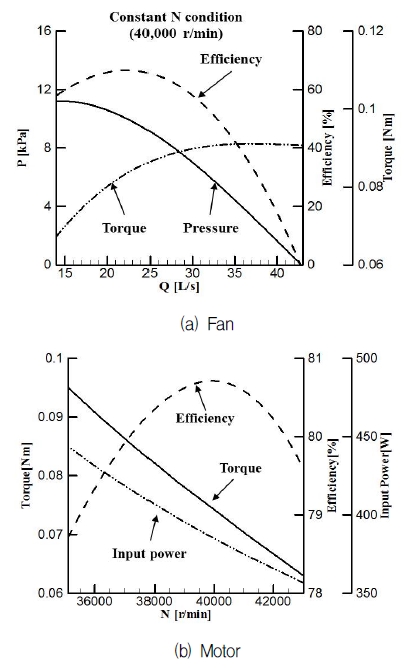
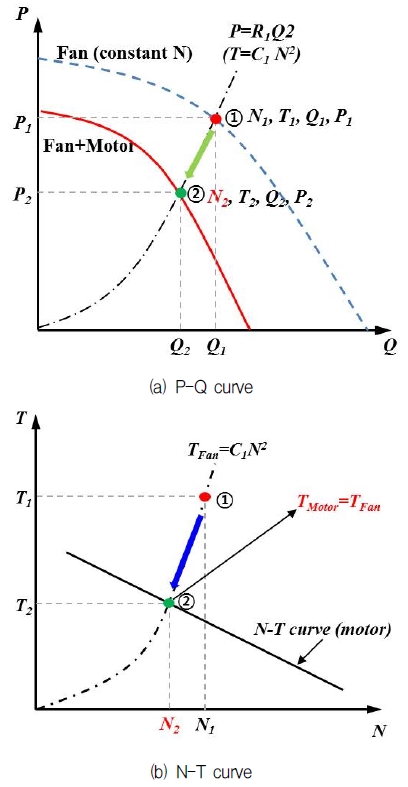
축동력은 회전속도 N과 토크 T의 곱으로 표현되고, 유체 에너지는 압력 P와 유량 Q의 곱으로 표현되며 흡입일률(suction power)이라고 부른다. 팬 특성곡선은 Fig. 4(a)와 같이 유량에 따른 압력, 토크, 효율( ηFan) 등의 관계를 그래프로 표현한 것이다. 이 때 일반적으로 회전속도 N은 일정한 값을 사용하여 팬의 특성을 표현한다.
팬 법칙(fan law)에 의해 회전속도 및 팬의 직경(D) 변화에 따른 팬의 특성변화를 알 수 있는데, 유량, 압력, 파워에 대하여 아래 식 (2)~(4)와 같은 관계를 가진다.(10)
| (2) |
| (3) |
| (4) |
팬 법칙은 레이놀즈수나 마하수의 변화가 없고 완벽한 기하학적 상사가 만족될 때 성립한다. 그러나, 이러한 제한에도 불구하고 팬의 직경, 회전속도의 변화에 대해 상당한 수준의 정확한 값을 예측한다.(10)
유동저항에 의한 압력강하(PR)는 식 (5)와 같이 유량의 제곱에 비례하며, 팬 특성곡선 상에서 시스템의 유동저항 곡선으로 표현된다. 유동저항 곡선(flow resistance curve)과 팬의 P-Q 곡선이 만나는 점에서 실제로 팬이 작동하게 되고 이를 팬의 작동점이라고 한다.
| (5) |
팬이 임의의 시스템에 장착되어 작동될 때 시스템의 특성인 유동저항에 의해 저항곡선이 결정되는데, 이를 일정 교축조건(constant throttling condition)이라고 부른다. 흡입일률 시험 시 특정 오리피스 사이즈에서 팬이 작동하는 경우도 일정 교축조건이 된다. 팬의 회전속도가 변동되는 경우, 식 (2)와 (3)으로부터 P∝Q2의 관계가 성립하는데, 이는 식 (5)의 유동저항 곡선과 같은 형태이다. 이는 팬의 회전속도 변화 시 팬의 특성은 일정 교축조건 즉, 동일한 유동저항 곡선상에서 변화하게 됨을 의미한다. 추가적으로, 팬 법칙에 의해 팬의 회전속도 변화 시 작동점의 효율 변화도 없기 때문에BEP의 오리피스 직경은 변하지 않게 된다.
표준 공기조건에서 오리피스를 통과하는 유량은 다음 식으로 표현된다.(8)
| (6) |
식 (6)에서 Q의 단위는 L/s, P의 단위는 kPa이다. 여기에서 오리피스 계수 α는 다음과 같이 정의된다.
| (7) |
s : the thickness of the orifice plate [mm]
d : the orifice diameter [mm]
식 (6)과 (7)을 오리피스 직경에 대해 정리하면 다음의 2차 방정식으로 나타낼 수 있다.
| (8) |
식 (8)의 해를 구함으로써, 팬 특성 곡선 상의 임의의 점에서 압력과 유량 값으로부터 그 점의 교축조건에 해당하는 오리피스 직경을 알 수 있다. 본 연구에서는 두께 2 mm의 오리피스 플레이트가 사용되었다.
모터의 효율은 식 (9)와 같이 입력전력(Pin)과 축동력(NT)으로 표현된다. 모터의 특성 곡선은 Fig. 4(b)와 같이 회전수(N)에 대해 토크, 입력전력, 효율(ηmotor)등을 표현한다.
| (9) |
전자기 설계에 의해 모터의 전압상수(voltage constant)와 토크상수(torque constant)가 결정되면 모터의 특성이 결정된다.(11) SRM의 경우 입력 전류의 제어각인 선행각(advance angle)과 도통각(dwell angle)의 변화에 의해서도 모터상수가 달라지는데, 전류 제어각이 변화되면 모터의 N-T 특성이 변화되고 이에 따라 효율 특성도 변하게 된다.(12)
3.2 System-level analysis
입력전력에 의해 모터가 토크를 발생시켜 팬을 회전시키는데, 이 때 팬-모터 어셈블리는 시스템의 유동저항에 의해 작동점이 정의된다. 시스템의 성능이 최적 상태가 되기 위해서는, 팬-모터 어셈블리가 작동점에서 최고효율점(Best efficiency point, BEP)을 가져야 한다. Bypass 타입의 경우 팬-모터 어셈블리의 효율은 식 (10)과 같이 팬과 모터의 효율의 곱으로 표현된다. 따라서, 팬과 모터는 각각 팬-모터 어셈블리의 작동점에서 BEP를 가지도록 설계되어야 한다.
| (10) |
본 연구에서 다루는 through-flow 타입 모터의 경우에는 bypass 타입의 효율에 모터의 유동저항의 영향을 추가로 고려하여야 한다. 또한, 시스템의 특성에서는 전공청소기의 유동저항의 영향이 고려되어야 한다. 결국 팬, 모터, 모터의 유동저항 그리고 진공청소기의 유동저항의 상호작용이 고려되어야 최종적으로 휼륭한 성능의 진공청소기 개발이 가능하다.
식 (10)에서 알 수 있듯이 어셈블리나 시스템의 특성은 입력전력(Pin), 회전속도(N), 토크(T), 압력(P), 유량(Q)의 5가지 변수로 대표되어지며, 유동저항에 의한 압력강하로 어셈블리나 시스템의 효율은 식 (10)보다 낮은 값을 가지게 된다. 결국, Fig. 2와 같이 어셈블리는 “모터+팬+모터의 유동저항”으로 구성되고, 시스템은 “어셈블리+진공청소기의 유동저항”의 형태이므로, 모터, 팬, 그리고 유동저항의 상호작용에 의한 특성변화를 알면 어셈블리나 시스템의 특성을 예측할 수 있다.
이번 절에서는 모터의 유동저항은 고려하지 않고 팬과 모터가 결합된 “팬+모터”의 특성을 구하는 방법을 설명하고자 한다. 팬+모터가 작동 시, 팬의 토크와 모터의 토크는 항상 일치해야 한다.(13) 즉, 팬과 모터 특성의 공통인자인 회전속도(N)와 토크(T)에 대해 두 인자가 같게 되는 특성을 찾아야 한다. 앞에서 언급한 대로, 일정 교축 조건에서는 팬의 회전속도 변화에 의한 팬 법칙를 이용하여 팬 특성 변화를 예측할 수 있다. 식 (4)로부터 회전속도 변화 시 팬의 토크는 다음 같이 회전수의 제곱에 비례한다는 것을 알 수 있으며, C는 비례상수이다.
| (11) |
Fig. 5(a)에 일정 회전속도 상태인 팬의 특성곡선(점선)을 나타내었다. 임의의 한 점 ①에서의 팬의 특성을 N1, T1, P1, Q1이라고 하면, Q1과 P1값을 이용하여 식 (5)로부터 점 ①의 일정 교축조건(R = R1)을 결정할 수 있다. 점 ①에서의 팬의 특성인 N1, T1을 Fig. 5(b)와 같이 모터의 N-T 곡선 위에 표시하면, 일반적으로 모터의 N-T곡선 위에 존재하지 않을 것이다. 정해진 교축조건에서 팬의 토크는 식 (11)과 같이 포물선 형태(T = C1N2)를 가지는데, 이 곡선과 모터의 N-T 곡선이 만나는 점, 즉 팬의 토크와 모터의 토크가 일치하는 점 ②를 찾을 수 있다.(13) 점 ②에서의 N2, T2가 주어진 교축조건에서 팬과 모터의 토크 매칭(torque matching) 되는 값이며, 이 값으로부터 팬 법칙를 적용하면 팬+모터의 P2, Q2를 다음과 같이 얻을 수 있다.
| (12) |
| (13) |
이러한 과정을 교축조건을 바꿔가며 각 조건별 팬과 모터의 토크 매칭 조건을 찾으면, Fig. 5(a)에서처럼 팬+모터의 특성곡선(실선)을 얻을 수 있다. 추가로, 유량 별로 결정된 회전속도로부터 모터의 입력전력이 결정되어, 팬+모터의 주요 특성들(N, T, P, Pin)은 모두 유량(Q)만의 함수로 표현이 된다.
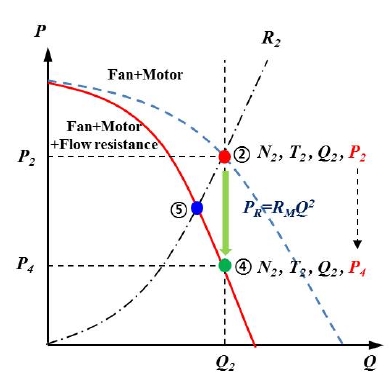
앞 절에서 구한 팬+모터의 특성에 추가로 유동저항의 영향을 살펴보려고 한다. 다시 말해 팬+모터에 유동저항이 결합된 등가 팬+모터(equivalent fan+motor)의 특성을 구하는 것이라고 볼 수 있다.(10) Fig. 2에서 일정한 유량이 흐른다고 가정하면, 팬+모터는 유동저항의 유/무와 상관없이 앞절에서 구한 특성대로 작동을 하게 될 것이다. 즉, 등가 팬+모터는 유동저항에 의해 압력(P)만 변화하고 회전속도(N), 토크(T), 유량(Q), 입력전력(Pin) 등의 특성은 원래의 팬+모터의 특성을 유지하게 된다. 따라서 Fig. 6의 팬+모터의 특성곡선 위의 한 점 ②는 동일한 유량 조건에서 모터의 유동저항에 의해 압력만 점 ④의 압력 P4로 변한다.
| (14) |
이러한 과정을 유량을 변경해가며, P-Q곡선 위의 모든 점에 대해 수행하면 유동저항을 고려한 특성 곡선을 얻을 수 있다.
앞서 언급한 토크 매칭(팬+모터)과 모터 유동저항에 의한 영향을 결합하면 최종 어셈블리 특성을 예측할 수 있다. 이때 앞선 설명의 순서와 다르게, 유동저항의 영향을 먼저 고려하고 토크매칭을 나중에 고려하여도 같은 결과를 가진다.(6) 어셈블리의 특성에 추가로 시스템의 유동저항 Rs의 영향을 고려하면 시스템의 특성을 얻을 수 있다.
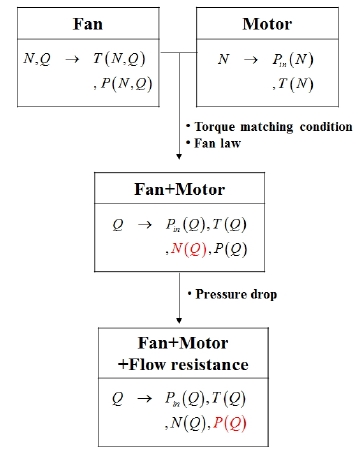
Fig. 7에 시스템-레벨분석 방법의 개념도를 나타내었다. 팬의 특성은 식 (1)에서 나타난 바와 같이 N, Q, P(N,Q), T(N,Q)의 4개의 변수로 결정이 되며, N과 Q가 독립변수이다. 모터의 특성은 식 (9)에서와 같이 N, Pin(N),T(N)의 3개의 변수로 결정이 되며, 이 때 N을 독립변수로 가진다. 토크매칭 조건과 팬 법칙을 이용하여 얻어지는 팬+모터의 특성은 1개의 독립변수 Q에 대해 나머지 4개의 변수 Pin, T, N, P가 정해진다. 팬+모터의 특성에 모터 또는 시스템의 유동저항을 고려하면 최종적으로 어셈블리나 시스템의 특성을 얻을 수 있는데, 이 때는 식 (14)에서와 같이 팬+모터의 특성에서 압력만 변화하기 때문에, 독립변수 Q만 결정되면 나머지 4개의 특성도 결정할 수 있다.
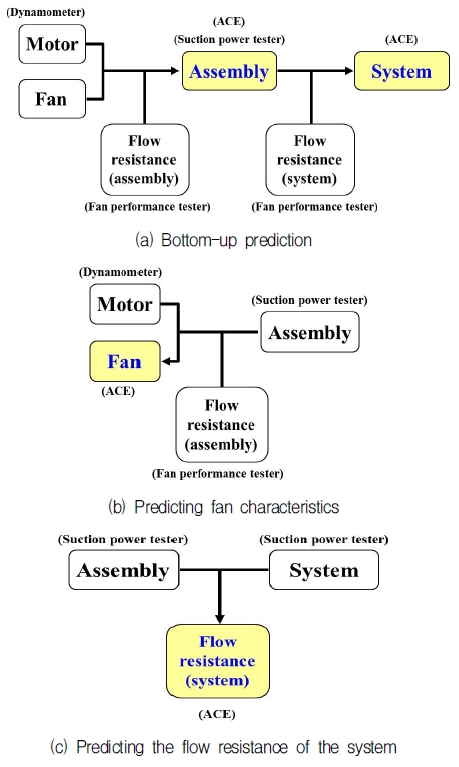
Park(6) 등은 위에서 언급한 설계기술을 구현하기 위해 팬-모터 특성예측 프로그램 ACE(Air-moving Characteristics Estimation)를 개발하였다. ACE를 이용하여 Fig. 8(a)와 같이 개별 컴포넌트의 특성으로부터 상위시스템(어셈블리 & 시스템)의 성능 예측이 가능하다. 청소기용 팬-모터 어셈블리의 경우 팬만의 특성을 측정하기 쉽지 않은데, Fig. 8(b)와 같이 어셈블리와 모터 성능, 그리고 모터의 유동저항 값으로 부터 팬만의 성능을 추출할 수 있다. 또한, Fig. 8(c)와 같이 시스템의 유동저항 값을 팬 성능 시험장치를 이용한 별도의 실험을 하지 않고도 어셈블리와 시스템의 성능으로부터 계산해 낼 수 있는 등 다양한 용도로 활용 가능하다.
4. ACE를 이용한 청소기 모터의 분석
Park(6) 등은 ACE의 검증을 위하여 유동저항용 테스트 지그를 이용하여 ACE의 시스템 특성 예측능력을 검증하였다. 본 연구에서는 실제 진공청소기 시스템에 S2 모델을 장착하고 시스템의 특성과 ACE의 예측결과를 비교, 분석하였다. 또한, 어셈블리의 특성에 모터의 유동저항이 미치는 영향에 대해 고찰하고, S2 모델의 모터 유동저항을 감소시킨 수정 모델에 대해 어셈블리의 효율 증가를 실험으로 확인하였다. 이를 위해 어셈블리나 시스템의 성능은 흡입일률 시험기로 측정하였고, 다이나모미터를 이용하여 모터의 성능을 측정하였다. 또한, 팬 성능 시험장치를 이용하여 모터와 진공청소기의 유동저항을 측정하였다.
4.1 진공청소기 시스템 성능 예측
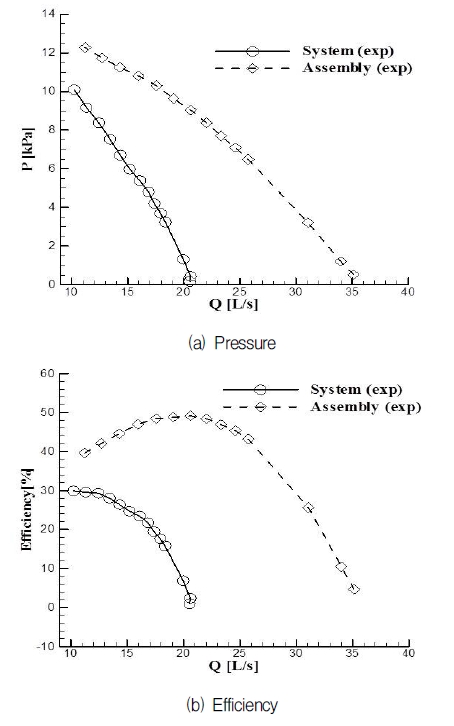
S2 모델을 Upright형 진공청소기에 장착하여 시스템의 성능을 흡입일률 시험기로 측정하였다. Fig. 9에 어셈블리와 시스템의 압력-유량 곡선과 효율-유량 곡선을 나타내었다. 유동저항에 의해 식 (14)와 같이 유량별 압력 감소가 나타나고, 그에 따른 흡입일률(PQ)의 감소가 발생하여 Fig. 9(b)와 같이 효율의 감소가 나타난다.
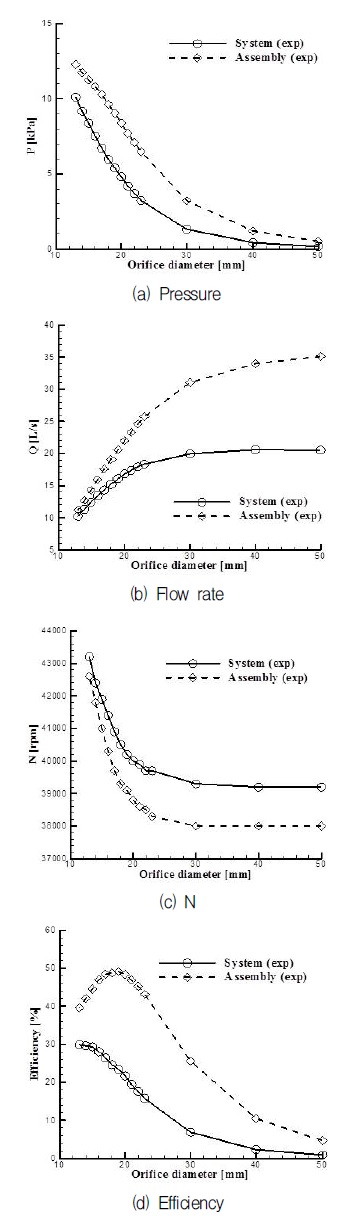
Fig. 10에는 오리피스 직경을 x축의 변수로 하여 어셈블리와 시스템의 특성을 비교하였다. Fig. 10(a)와 (b)에서 동일 오리피스 직경에 대해 유동저항에 의한 영향으로 압력과 유량 모두 감소하는 것을 알 수 있고, 결국 이는 흡입일률의 감소로 이어진다. Fig. 10(c)에서 동일 오리피스 기준 시스템의 회전속도가 증가한 것을 알 수 있는데, 이는 모터의 주요 변수인 회전속도의 변화로 시스템의 특성에서 토크와 입력전력의 변화가 생긴다는 것을 의미한다. 본 연구에서 다룬 SRM의 경우, Fig. 4(b)에서 알 수 있듯이 회전속도의 증가에 따라 입력전력과 토크가 감소하는 특성을 가진다. 즉, 시스템의 효율 관점에서 입력전력 및 흡입일률 모두 감소한다는 것을 알 수 있다. Fig. 10(d)로부터 어셈블리에 비해 시스템의 효율이 감소한 것을 알 수 있는데, 이는 입력전력의 감소보다 흡입일률의 감소가 커서 나타남을 알 수 있다.
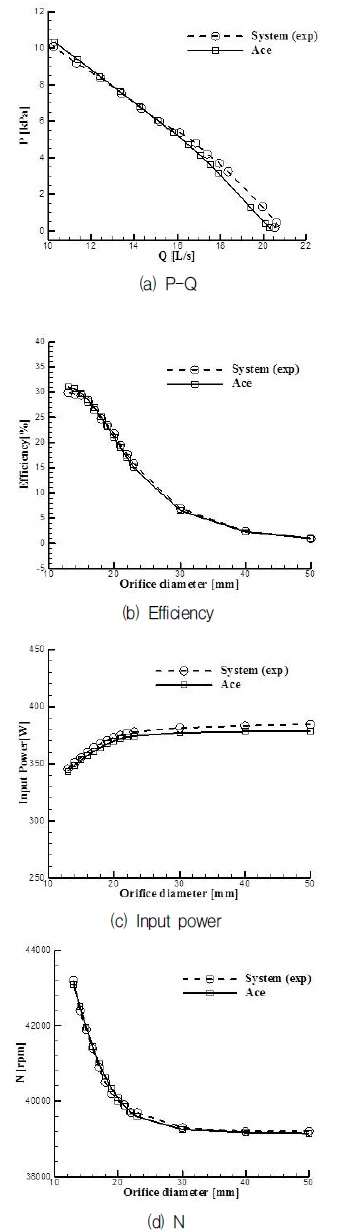
ACE를 이용하여 어셈블리 특성과 시스템의 유동저항 값으로부터 시스템의 특성을 예측하였고(Fig. 8(a) 참고), Fig. 11에 그 결과를 나타내었다. 팬 성능 시험장치로부터 측정된 시스템의 유동저항 계수 Rs=0.021823 kPa/(L/s)2이 이용되었다. 예측값은 압력은 4.5 % 이내, 효율은 6 %이내에서 실험과 잘 일치하고 있으며, 입력전력이나 회전속도도 2 %이내에서 실험값과 잘 일치한다. 이를 통해 ACE는 실제 진공청소기 시스템의 성능 예측도 정확하게 예측함을 확인하였다. 단지, 고유량 영역에서 실험값과 차이가 커짐을 알 수 있는데, 이는 크게 두 가지의 원인에 기인하는 것으로 추정된다. 첫째는 팬 성능 시험장치를 통한 시스템의 유동저항 측정 시 팬에 의한 속도의 회전(swirl) 성분이 고려되지 않기 때문에 실제 값과 예측에 사용된 값에 차이가 존재할 것이다. 또한, 흡입일률 시험에 사용되는 오리피스 직경의 간격이 고유량 영역에서 크기 때문에 이에 의한 보간 오차가 증가하기 때문으로 보인다.
4.2 모터의 유동저항이 어셈블리에 미치는 영향 고찰
어셈블리의 효율을 최대화하기 위해서는, 어셈블리의 BEP에서 팬과 모터도 BEP를 가져야 한다. 또한, 모터의 유동저항을 최소화해서 유동저항에 의한 압력 감소 및 그에 의한 효율의 저하를 최소화 해야 한다. ACE를 어셈블리의 흡입일률 시험과 모터의 다이나모미터 실험, 그리고 팬 성능 시험장치를 이용한 모터의 유동저항 측정값으로부터 팬만의 성능을 추출할 수 있다(Fig. 8(b) 참고). 이를 이용하여 모터의 유동저항이 없는 경우인, 팬+모터의 성능을 ACE를 이용하여 예측하고 이를 어셈블리의 성능과 비교하면 모터의 유동저항이 어셈블리의 성능에 미치는 영향을 파악할 수 있다. 이전 연구에서 S2 모델은 팬과 모터의 BEP는 잘 일치하나, 모터의 유동저항에 의한 어셈블리의 효율 감소가 4.7% 수준(BEP의 오리피스 기준)으로 타 모델에 비해 큼을 확인하였다.(6)
주어진 유량에서 유동저항에 대한 어셈블리의 효율감소는 Fig. 6의 점 ②와 ④의 관계를 살펴보면 알 수 있다. 점 ④에서는 점 ②에서 압력강하만 나타나기 때문에, 점 ④에서의 효율은 다음 식으로 표현된다.
| (15) |
이 식을 점 ②에서 ④로의 효율 감소 △η에 대해 쓰면 식 (16)과 같이 나타낼 수 있으며, 이 때 R2는 점 ②에서의 일정 교축 조건의 유동저항 계수이다.
| (16) |
결국, 팬+모터에서 모터의 유동저항에 의한 효율 감소는 주어진 점에서 일정 교축조건의 유동저항계수 RΦ와 모터의 유동저항 계수 RM의 비로 나타내어 지며, 편의상 이 값을 유동저항비(the flow resistance ratio, FRR)라고 부르겠다. 실제 어셈블리의 특성을 고려할 때, 오리피스 기준으로 효율 변화를 주로 다루는데, 이는 Fig. 6에서 점②에서 ⑤로의 효율 변화를 알아야 한다.
Table 1에 3가지 어셈블리 모델의 BEP에서 유동저항에 의한 효율 감소와 관련 변수들을 나타내었다. Table 1의 마지막 행의 BEP 오리피스에서 효율 감소는 ACE를 이용하여 예측한 팬+모터의 효율과 실제 어셈블리의 효율 측정값의 차이를 나타내는데, 모터의 유동저항에 의한 BEP에서의 어셈블리의 효율 감소를 의미한다. S1 모델은 직경 105 mm의 2D 팬으로 43,000 rpm으로 회전하는 모델이고, S3 모델은 직경 56 mm의 3D 팬으로 89,000 rpm으로 회전하는 모델이다.(6,14) 모터의 유동저항 값만 비교하면 S1 모델에 비해 S2 모델은 약 3배, S3 모델은 약 6배가 크지만 실제 어셈블리의 효율 감소는 S2 모델에서 가장 크게 나타난다. 이는 효율감소가 식 (16)의 FRR에 의해 결정되기 때문에 저유량 영역에서 BEP를 가지는 S3 모델에 비해 S2 모델의 효율 감소가 크게 나타나는 것이다. Table 1의 5행의 FRR과 6행의 BEP 오리피스에서의 효율감소 값을 비교해 보면, 유동저항비가 일정 유량조건에서의 효율감소를 나타내지만, 오리피스 기준의 효율 감소의 정성적인 지표로도 사용가능함을 짐작할 수 있다. 따라서, 팬-모터 어셈블리에서 FRR은 모터의 기구적인 설계 시 고려되어야 하는 유용한 인자로 사용될 수 있을 것이다.
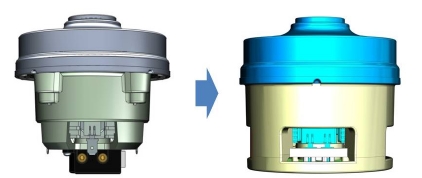
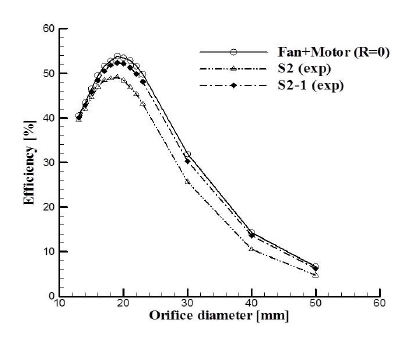
Fig. 12에 모터의 유동저항을 감소시키기 위하여 S2 모델과 동일한 모터 코어에 하우징 설계만 수정한 S2-1모델의 형상을 나타내었다. S2-1 모델은 모터의 유동저항 계수가 5.27E-04 kPa/(L/s)2으로 BEP에서의 FRR 값을 2.4% 수준으로 개선한 모델이다. Fig. 13에 ACE로 예측한 팬+모터의 효율과 흡입일률 시험으로 측정한 S2모델과 S2-1모델의 효율을 비교하였다. S2-1 모델은 S2 모델에 비해 어셈블리의 BEP 효율이 3.2% 상승하였고, S1과 S3 모델처럼 이상적인 경우인 팬+모터의 효율에 비하여 효율 감소가 1% 수준대로 성능이 개선되었다.
5. 결 론
본 연구에서 ACE를 이용한 진공청소기용 팬-모터 어셈블리의 시스템-레벨분석을 수행하였다. 팬-모터 어셈블리의 특성과 진공청소기 시스템의 유동저항 계수를 이용하여 시스템의 성능특성을 예측하였고, 예측된 결과는 실제 진공청소기의 성능 측정을 통해 검증하였다. ACE의 예측결과는 압력은 4.5% 이내, 효율은 6 % 이내에서 실험 결과와 잘 일치하였다. 또한, 모터의 유동저항이 팬-모터 어셈블리의 성능에 미치는 영향을 일정 유량조건에서 모터의 유동저항과 일정 교축조건의 유동저항의 비로 정의되는 FRR 값으로 정량화할 수 있으며, FRR은 오리피스 직경 기준의 효율 감소를 고려할 때에도 정성적인 설계 변수로 활용 가능하다는 것을 확인하였다. 모터의 유동저항에 의해 어셈블리의 효율 감소가 큰 S2 모델의 FRR 값을 9.0%에서 2.4% 수준으로 개선한 모델의 성능 평가를 통해 실제 팬-모터 어셈블리의 효율 증가를 확인하였다.
References
- Biček, A., Markič, I., Rihtaršič, J., Rejec, J., and Čudina, M., (2014), “Vacuum Cleaner Suction Unit Performance and Noise Characterization–an Overview,”, 6th congress of Alps-Adria Acoustics Association, Graz, Austria.
- European Commission, https://ec.europa.eu/energy/en/topics/energy-efficiency/energy-efficient-products
-
Epple, P., Karic, B., Llič, Č., Becker, S., Durst, F., and Delgado, A., (2009), “Design of Radial Impellers: A Combined Extended Analytical and Numerical Method,” Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 223, p901-917.
[https://doi.org/10.1243/09544062jmes1196]

- Herber, A. J., and Li, J., (1995), “Predicting Variable-speed Fan Performance from Motor and Impeller Characteristics, Part I. Using Complete Motor Data,”, American Society of Agricultural Engineering, 38(4), p1247-1252.
- Lin, S. C., and Tsai, M. L., (2012), “An Integrated Performance Analysis for a Backward-inclined Centrifugal Fan,”, Computers & Fluids, 56, p24-38.
- Park, C. H., Jun, S. O., Park, K. H., Lee, S. J., and Chang, K. S., (2015), “Methodology for System-level Analysis of a Fan-motor Design,” Published online in Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, http://journals.sagepub.com/doi/full/10.1177/0954406216651650.
- Li, H., (2009), “Fluid Flow Analysis of a Single-Stage Centrifugal Fan with a Ported Diffuser,”, Engineering Applications of Computational Fluid Mechanics, 3(2), p147-163.
- IEC 60312-1, (2010), Vacuum Cleaners for Household Use–Part 1: Dry Vacuum Cleaners - Methods of Measuring Performance, International standard, The International Electrotechnical Commission (IEC), Edition 1.0.
- ANSI/AMCA 210-99, (1999), Laboratory Methods of Testing Fans for Aerodynamic Performance Rating, Air Movement and Control Association, Inc.
- Osborne, W.C., (1977), FANS, 2nd ed., Pergamon Press, Oxford.
- Hubert, C. I., (2009), Electric Machines: Theory, Operation, Applications, Adjustment, and Control, 2nd ed., Pearson Education, New York.
- Miller, T. J. E., (1993), Switched Reluctance Motors and Their Control, Hillsboro, Magna Physics pub., OH.
- Eck, B., (1973), Fans: Design and Operation of Centrifugal, Axial-flow, and Cross-flow Fans, Pergamon Press, Oxford.
- Jung, U. H., Kim, J. H., Kim, J. H., Park, C. H., Jun, S. O., and Choi, Y. S., (2016), “Optimum Design of Diffuser in a Small High-speed Centrifugal Fan Using CFD & DOE,”, Journal of Mechanical Science and Technology, 30(3), p1171-1184.