세미 플로팅 링 베어링으로 지지된 터보차저의 Subsynchronous 진동 특성
Abstract
The small turbocharger for the automotive application is designed to operate up to 200,000 rpm to increase system efficiency. Because of high rotation speed of turbocharger, floating ring bearing are widely adopted due to its low friction loss and high rotordynamic stability. This paper presents a linear and nonlinear analysis model for a turbocharger rotor supported by a semi-floating ring bearing. The rotordynamic model for the turbocharger rotor was constructed based on the finite element method and fluid film forces were calculated based on the infinitely short bearing assumption. In linear analysis, we considered fluid film force as stiffness and damping element and in nonlinear analysis, the fluid film force was calculated by solving the time dependent Reynolds equation. We verified the developed theoretical model by comparing to modal test results of test rotors. The analysis results show that there are two unstable modes, which are conical and cylindrical modes. These unstable modes appear as sub-synchronous vibrations in nonlinear analysis. In nonlinear analysis, frequency jump phenomenon demonstrated when vibration mode is changed from conical mode to cylindrical one. This jump phenomenon was also demonstrated in the test. However, the natural frequency measured in the test differs from those obtained using nonlinear analysis.
Keywords:
Floating Ring Bearing, Stability, Turbocharger키워드:
플로팅링 베어링, 안정성, 터보차저1. 서 론
자동차용 내연 기관에 적용되는 소형 터보차저는 연소 시 생성되는 고온의 배기가스를 이용하여 터빈을 회전시키고 이를 동력원으로 압축된 공기를 내연 기관에 공급하여 출력을 향상시키는 역할을 한다. 터보차저의 적용만으로 내연기관의 연비 및 출력 향상이 가능 하므로, 계속 강화되는 연비 규제에 대응하기위해 이에 대한 개발과 적용이 계속 증가하고 있다. 자동차용 소형 터보차저는 특히 터빈과 압축기의 고 효율 영역에서의 운전을 위해 회전 속도를 최대 200,000 rpm 이상에서 운전 되도록 설계하고 있으며, 이러한 고속운전에 대응하기 위해 대부분 플로팅 링 베어링을 적용하고 있다.(1)
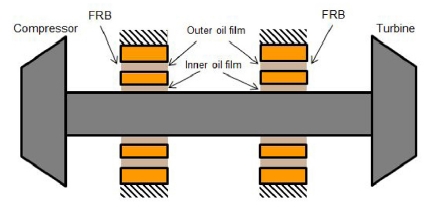
플로팅 링 베어링은 Fig. 1과 같이 링의 내 외측에 위치한 2개의 윤활 막이 회전축을 지지하는 베어링으로서, 구름 베어링 보다 적은 마찰 손실을 가지며, 일반적인 플레인 저널 베어링에 비해 높은 동적 안정성을 가진다. 이러한 플로팅링 베어링은 내측 유막과 외측 유막 사이에 위치한 링의 회전 여부에 따라 풀 플로팅 링 베어링과 세미 플로팅 링 베어링으로 분류할 수 있다. 풀 플로팅 링 베어링은 링에 전달되는 윤활유의 점성마찰에 의해 자유롭게 회전할 수 있는 구조를 가지며, 세미 플로팅 링 베어링은 외부 장치에 의해 이러한 링의 회전을 구속하는 구조를 가진다. 현재 자동차용 소형 터보차저에는 상기의 2가지 타입 모두 적용이 되고 있다.
플로팅 링 베어링에 대한 초기 연구는 주어진 운전 조건에서 회전축과 링의 정적 평형 위치를 계산하거나, 선형화된 유막의 강성, 감쇠 계수를 이용하여 여러 운전 조건에서 시스템의 동적 특성을 예측하는 연구들이 많이 이루어졌다.(2-4) 이러한 연구들은 플로팅 링 베어링의 동작 원리를 이해하고 이를 적용한 시스템을 설계하는데 유용한 설계 도구로 사용되었다. 플로팅 링 베어링이 적용된 자동차용 터보차저에 대한 연구는 주로 유체 베어링의 불 안정성으로 인해 나타나는 Sub-synchronous 진동을 관찰하거나 이론적으로 고찰하는 연구가 많이 진행되어 왔다. 주로 선형 해석 이론을 통한 로터 베어링 시스템의 모델링을 통하여 시스템이 가지는 불 안정 모드를 예측하거나,(5) 실험을 통하여 회전속도에 따라 다르게 나타나는 진동 특성을 파악하는 연구들이 보고되었다.(6) 특히, 실험을 통하여 일반적인 회전 기계와는 다르게 여러 개의 주파수 성분을 가진 Sub-synchronous 진동이 동시에 나타나거나, 회전 속도에 따라 특정 주파수 진동이 없어지거나 나타나는 Jump현상이 보고되기도 하였다. 이러한 Sub-synchronous 진동은 비선형 해석을 통해 이론적으로 예측이 가능함이 보고되었으며,(7-9) 비선형 해석모델을 통해 로터 베어링 외부의 가진에 의한 회전축 진동의 영향을 예측하는 연구들이 수행 되었다.(10) 그러나, 이러한 연구들은 주로 풀 플로팅 링 베어링 대해 수행 되었으며, 세미 플로팅 링 베어링이 적용된 터보차저 시스템에 대한 연구는 상대적으로 적게 수행되었다.
본 연구는 세미 플로팅 링 베어링으로 지지된 터보차저 로터의 선형 및 비선형 해석 모델을 통하여, 불 안정성으로 인해 나타나는 Sub-synchronous 진동 특성에 대해 예측 하고, 이를 실험과 비교함으로서 해석 모델을 검증하고자한다.
2. 연구 방법
2.1 해석 모델
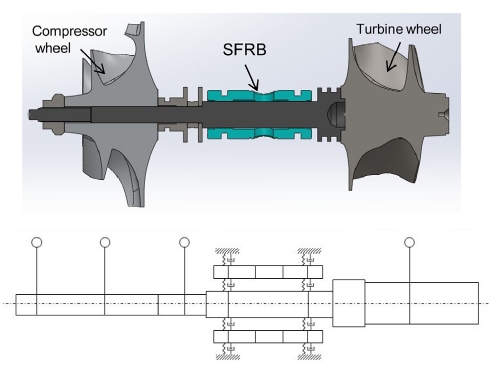
Fig. 2는 해석 대상이 되는 터보차저의 단면과 이에 대한 해석 모델을 나타낸다. 해석 대상은 로터 양단에 터빈과 압축기 휠이 연결되어 있는 형상이며, 회전축 중심에 위치한 세미 플로팅 링 베어링이 로터를 지지하는 구조이다. 플로팅 링 중심에는 시스템에 조립되었을 때 링의 회전을 방지하는 핀이 삽입되는 홀이 존재하게 된다. 로터베어링 시스템의 운동 방정식은 식 (1)과 같은 형태를 가지며, 유한 요소법을 통해 계산된 질량(M), 자이로스코픽(J), 강성(K), 감쇠(C)행렬로 구성된다.
| (1) |
로터는 Fig. 2에 표시된 각 노드에 집중 질량 요소가 강성 요소로 연결된 형태로 모델링 되었으며, 압축기와 터빈 휠은 관성 요소로 취급되었다. 각 노드는 수직, 수평 방향에 대한 변위와 회전의 4개의 자유도를 가진다. 로터에 대한 강성 행렬은 Euler의 보 이론으로부터 유도 되었다.(11) Table 1은 로터를 구성하는 각 부품과 해석에 사용된 물성치를 나타낸다.
플로팅 링 베어링은 Fig. 1과 같이 로터를 2개의 유막이 지지하는 형태를 가진다. 베어링 내부에서 발생하는 압력은 무한 소폭 베어링 가정을 통해 식 (2)의 지배 방정식을 통해 계산이 된다.(12)
| (2) |
상기 식을 통해 베어링 내 유막에서 발생하는 압력이 계산이 되며, 이를 통해 로터에 작용하는 유막력이 계산이 된다. 본 연구에서는 유막력을 선형 강성, 감쇠요소로 모델링하여 식 (1)의 강성, 감쇠 행렬에 포함 시켜 계산하는 선형 해석 방법과, 식 (2)의 시간의 함수로 주어지는 내측, 외측의 유막 압력을 적분하여 식 (1)의 외력 항에 포함시켜 로터의 운동을 계산하는 비선형 해석 방법을 통해 로터의 동적 특성을 예측하였다. 선형 해석에 사용되는 유막의 강성, 감쇠는 섭동법을 통해 계산이 된다.(12) 이러한 방법으로 선형 해석을 통해서는 회전속도에 따른 고유 진동수와 감쇠력을 결과로 제시하였고, 비선형 해석에서는 각 노드에서 시간의 함수로 나타나는 진동을 결과로 제시하였다. 비선형 해석에 관한 수치해석은 참고문헌(13,14)에 기술된 방법으로 수행 하였다.
2.2 실험 장치
본 연구를 통해 제시된 터보차저의 동적 거동에 대한 해석모델을 검증하기 위해 실험을 수행하였다.
Fig. 3는 전체 실험 장치의 구성을 나타낸다. 터보차저의 회전은 외부에서 공급 되는 압축 공기를 전기 히터를 이용하여 가열한 후 생성되는 고온, 고압의 압축공기를 터빈에 공급하는 방식으로 수행 되었다. 터빈에 공급되는 압축 공기의 온도는 500℃이며, 터보차저의 흡기구로 유입된 대기압 상태의 공기는 압축기를 거친 후, 별도로 연결된 토출 라인을 따라 외부로 배출된다. 터빈과 압축기 입, 출구에서 센서를 통하여 압력과 유량을 모니터링 하게 된다. 터보차저 회전 시 오일 펌프 통하여 베어링에 윤활유를 공급하게 되며, 진동을 측정하기 위해 Fig. 4와 같이 압축기 휠 끝단에 2개의 레이저 변위 센서를 설치하였다. 실험에 사용된 레이저 변위 센서는 KEYENCE사의 LK-G80모델로서 1.4 mm/V의 민감도를 가진다. 터보차저의 회전 속도는 터빈으로 공급되는 고온의 압축 공기 유량을 조절함으로서 제어하였으며, 별도로 설치된 속도 센서를 통해 회전수를 기록하였다. 이러한 시스템을 통해 여러 회전속도 별 진동 크기를 측정하였다.
3. 연구 결과
3.1 로터 해석 모델 검증
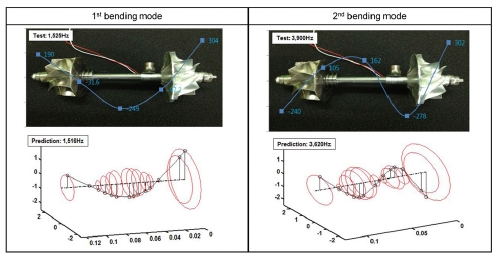
본 연구에서 제시된 로터의 유한 요소 해석 모델을 검증하기 위해 실험을 위해 제작된 터보차저 로터를 대상으로 가진 실험을 수행하였다. 임팩트 해머를 통해 로터를 가진 하였으며, 가속도계를 이용 축 방향 여러 위치에서 진동을 계측 하였다. Fig. 5는 실험을 통해 측정된 1, 2차 굽힘 모드의 모드 형상 과 고유 진동수를 해석 모델을 통해 예측한 결과와의 비교를 나타낸다. 그림을 통해 볼 수 있듯이, 해석 모델을 통해 예측된 모드 형상은 실험 결과와 유사하게 나타났다. 각 모드의 고유진동수는 1차 굽힘 모드의 경우 해석을 통한 예측 값이 1,516 Hz이고, 실험을 통해 측정된 값이 1,525 Hz로 두 값이 거의 일치하였으며, 2차 굽힘 모드의 고유진동수는 예측 값이 3,620 Hz, 실험 값이 3,900 Hz로 예측 결과가 측정 값에 비해 8% 정도 낮게 나타났다. 상기의 결과로 본 연구를 통해 제시된 로터의 해석 모델이 실제 제작된 로터의 동적 거동을 잘 예측함을 확인할 수 있었다.
3.2 로터 베어링 시스템 해석 결과
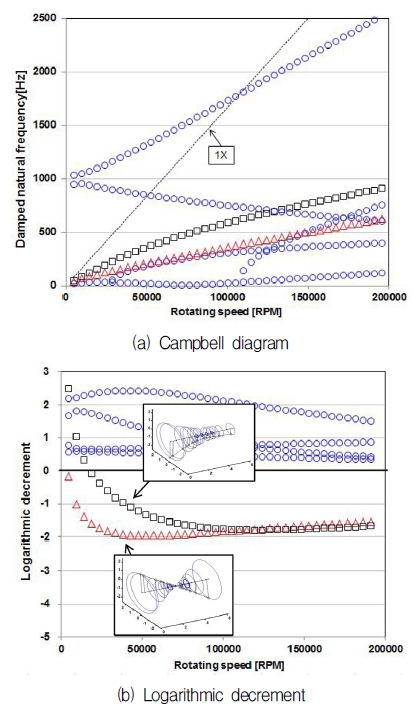
Fig. 6는 선형 해석 모델을 통해 계산된 터보차저 로터의 회전속도별 고유 진동수인 Campbell diagram과 각 진동 모드의 감쇠의 크기와 관련된 Logarithmic decrement이다. 해석 대상이 되는 로터와 베어링의 사양은 Table 2와 같다. 그래프의 수평 축은 터보차저의 회전 속도를 나타낸다. 그림을 통해 볼 수 있듯이 회전 속도 변화에 따라 각각의 모드가 가지는 고유 진동수가 변하는 것을 볼 수가 있다. 또한, Logarithmic decrement가 음수가 되는 불 안정 모드들은 200,000 rpm 이하에서 2가지가 나타났다. 이러한 불안정 모드는 Fig. 6-(b)에서 볼 수 있듯이 로터의 강체 모드와 관련된 병진 모드와 코니컬 모드인 것을 확인할 수 있다. 이렇게 세미 플로팅 링 베어링으로 지지된 터보차저 로터의 경우 내측 유막의 불안정성으로 인해 2가지의 불안정모드가 나타난 것으로 판단된다. 이러한 결과는 4가지의 불안정 모드가 나타나는 풀 플로팅 링 베어링의 경우와 비교하여 생각해 볼 수 있다.(9) 풀 플로팅 링 베어링의 경우 내, 외측 유막 모두 회전축의 불 안정성을 발생시키기 때문에 불 안정 모드는 링과 로터의 강체 모드가 조합된 형태로 모두 4가지 형태로 나타나게 된다. 반면, 세미 플로팅 링 베어링은 링이 회전하지 않기 때문에 내측 유막만이 불안정성에 기인하므로 로터의 강체 모드 2가지만 불안정 모드로 나타나게 된다. 본 연구의 해석 대상인 세미 플로팅 링 베어링의 경우 Fig. 6-(b)에서 볼 수 있듯이 회전 속도가 낮을 때는 코니컬 모드가 불 안정 영역에 존재하며, 회전 속도가 20,000 rpm 이상이 되면 병진 모드 또한 불안정 영역에 존재하는 것을 확인 할 수가 있다. 이러한 불안정 모드의 고유진동수는 Fig. 6-(a)에서 볼 수 있듯이 회전 속도 성분(1X) 보다 낮은 주파수 영역에 존재 하는 것을 볼 수가 있으며, 회전속도 증가에 따라 고유진동수 또한 증가함을 볼 수가 있다.
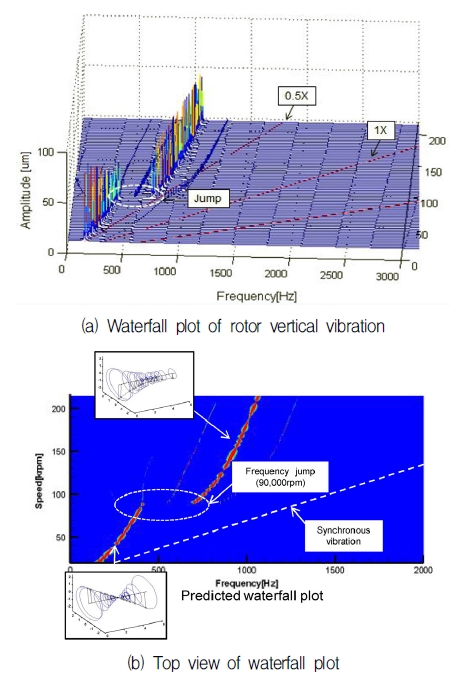
Fig. 7은 동일한 해석 대상에 대하여 비선형 해석 모델을 통해 예측된 Compressor 끝단의 수직 방향 진동에 대한 Waterfall 선도이다. 해석은 로터에 불 평형 질량이 없는 이상적인 경우를 가정하여 수행하였다. Fig. 7-(b)는 3차원 좌표계로 나타낸 Fig. 7-(a)를 수직 축 상에서 바라본 그림이다. 그래프를 통해 볼 수 있듯이 모든 회전 속도에서 1X 진동 이하에서 나타나는 Sub-synchronous 진동이 관찰 되었다. 이러한 진동은 회전 속도가 90,000 rpm이 되면 진동의 주파수가 갑자기 증가하는 Jump 현상이 관찰 되었다. 회전속도 별로 나타나는 진동 모드 또한 90,000 rpm 이하에서는 코니컬 모드로 나타났고, 90,000 rpm 이상에서는 병진 모드로 나타났다. 따라서, 진동 주파수가 바뀌는 Jump 현상은 진동의 모드가 바뀜에 따라 나타나는 현상으로 판단된다. 상기의 결과를 선형 해석 결과와 비교해 볼 때, 불안정 모드가 나타나는 순서는 Fig. 6-(b)를 통해 볼 수 있듯이 저속 영역에서 코니컬 모드가 불안정 영역에 먼저 존재하게 되고, 회전 속도가 증가함에 따라 병진 모드 또한 불안정 영역으로 이동하는 결과와 매칭 시킬 수 있다.또한, Jump 현상이 나타날 때 진동 주파수가 증가하는 현상은 Fig. 6-(a)에서 볼 수 있듯이 병진모드의 고유진동수가 코니컬 모드의 고유진동수보다 높기 때문에 진동 모드가 바뀔 때 이에 대응하는 고유 진동수가 나타나기 때문으로 판단된다. 그러나, 비선형 해석에서 Jump가 나타나는 회전속도인 90,000 rpm은 선형해석을 통해서는 예측할 수가 없었다. 또한, Table 3에서 볼 수 있듯이 선형 해석을 통해 예측된 불 안정 모드의 고유 진동수는 비선형 해석을 통해 예측된 결과보다 10~20% 정도 낮은 결과를 보였다. 이러한 선형 해석과 비선형 해석 결과의 차이는 유막력의 비 선형성에 기이한 것으로 판단된다.
3.3 실험 결과
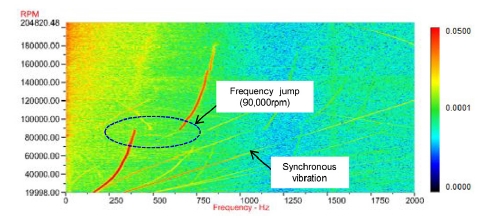
Fig. 8은 실험을 통해 측정된 Compressor 끝단의 수직 방향 진동에 대한 Waterfall 선도이다. 실험 결과 불균형 질량에 의해 나타나는 1X 진동에 비해 1X 이하에서 나타나는 Sub-synchronous 진동이 모든 회전속도에서 뚜렷하게 나타남을 확인할 수 있다. 이러한 Sub-synchronous 진동은 Fig. 7의 비선형 해석 결과와 비교할 때 전체적으로 유사한 경향을 보였으며, 90,000 rpm 부근에서 주파수가 크게 바뀌는 Jump 현상 또한 관찰 되었다. 이렇게 Jump 현상이 나타나는 회전속도는 Fig. 7-(b)를 통해 볼 수 있듯이 비선형 해석결과와 동일함을 확인할 수 있다. 그러나, 실험을 통해 측정된 진동 주파수는 Table 3을 통해 볼 수 있듯이 비선형 해석을 통해 예측된 결과와 5~15% 정도 차이를 나타났다. 이러한 해석과 실험 결과의 차이는 온도 영향에 의해 나타나는 실험과 해석에서 사용된 윤활유의 점도 차이나 열팽창 등에 의한 베어링의 간극 변화 등을 생각해 볼 수 있다. 이러한 원인에 대한 고찰은 향후 추가 해석을 통해 고찰해 볼 예정이다.
4. 결 론
본 연구에서는 세미 플로팅 링 베어링으로 지지된 터보차저 로터의 선형, 비선형 해석 모델을 통해 불안정성으로 인해 나타나는 Sub-synchronous 진동 현상을 예측하였고 실험을 통한 결과와 비교하였다. 로터 가진 실험을 통한 고유진동 모드 비교로 로터의 유한 요소 해석 모델을 검증하였고, 터보차저 구동 실험을 통해 전체 시스템에 대한 회전축의 진동을 관찰하였다.
세미 플로팅 링 베어링으로 지지된 터보차저 로터의 경우 2가지의 불안정 모드가 예측 되었고, 이는 로터의 강체 모드와 연관된 코니컬 모드와 병진 모드인 것으로 나타났다. 비선형해석을 통해 불안정성을 가지는 모드들이 회전 속도별로 다르게 나타남을 확인할 수 있었고, 진동 주파수가 갑자기 바뀌는 Jump 현상은 로터의 진동 모드가 바뀔 때 나타남을 유추할 수 있었다. 터보차저 실험을 통해 측정한 Sub-synchronous 진동은 비선형 해석을 통해 예측된 결과와 유사하게 나타났으며, 특히 Jump가 나타나는 회전속도가 잘 예측되었다. 이러한 결과를 토대로 비선형 해석을 통해 실제 로터의 거동이 예측 가능함을 확인할 수 있었다.
향후 추가실험을 통해 터보차저에 공급되는 공기의 온도 및 윤활유의 압력과 온도에 따른 회전축의 진동 특성에 대한 영향을 관찰할 예정이며, 추가 해석을 통해 세미 플로팅 링 베어링의 여러 가지 설계 변수에 대한 주파수 Jump현상에 대한 영향을 관찰할 예정이다.
Acknowledgments
본 연구는 한국기계연구원 기관 주요사업을 통해 수행되었습니다.
References
- Rohde, S. M., and Ezzat, H. A., (1980), “Analysis of Dynamically Loaded Floating-ring Bearings for Automotive Applications,”, Journal of Lubrication Technology, 102(3), p271-276.
- Orcutt, F. K., and Ng, C. W., (1968), “Steady-state and Dynamic Properties of the Floating-ring Journal Bearing,”, Journal of Lubrication Technology, 90(1), p243-253.
- Tanaka, M., and Hori, Y., (1972), “Stability Characteristics of Floating Bush Bearings,”, Journal of Lubrication Technology, 93, p248-259.
- Li, C. H., and Rohde, S. M., (1981), “On the Steady State and Dynamic Performance Characteristics of Floating Ring Bearings,”, J. of Lub. Tech, 103(3), p389-397.
- Schweizer, B., and Sievert, M., (2009), “Nonlinear Oscillations of Automotive Turbocharger Turbines,”, Journal of Sound and Vibration, 321(3), p955-975.
- Nakagawa, E., and Aoki, H., (1973), “Unbalance Vibration of a Rotor-bearing System Supported by Floating-ring Journal Bearings,”, Bulletin of JSME, 16, p503-512.
- Li, C. H., (1982), “Dynamics of Rotor Bearing Systems Supported by Floating Ring Bearings,”, Journal of Lubrication Technology, 104(4), p469-476.
- Childs, D., Moes, H., and Van Leeuwen, H., (1977), “Journal Bearing Impedance Descriptions for Rotordynamic Applications,”, Journal of lubrication technology, 99(2), p198-210.
- Lee, D., Kim, Y., and Kim, B., (2015), “Stability Analysis of Floating Ring Bearing Supported Turbocharger,”, Journal of the Korean Society of Tribologists and Lubrication Engineers, 31(6), p302-307.
- Tian, L., Wang, W. J., and Peng, Z. J., (2011), “Dynamic Behaviours of a Full Floating Ring Bearing Supported Turbocharger Rotor with Engine Excitation,”, Journal of Sound and Vibration, 330(20), p4851-4874.
- Chen, W. J., (2007), Introduction to Dynamics of Rotor Bearing Systmes, Chap. 5, Eigen Technologies, USA.
- Hamrock, B. J., (1994), Fundamentals of Fluid Film Lubrication, Chap.10, McGraw Hill, USA.
- Lee, D. H., Kim, Y. C., and Kim, K. W., (2007), “The Dynamic Performance Analysis of Foil Journal Bearings Considering Coulomb Friction: Rotating Unbalance Response,”, Journal of the Korean Society of Tribologists and Lubrication Engineers, 23(5), p219-227.
- Tian, L., (2012), Investigation into Nonlinear Dynamics of Rotor-Floating Ring Bearing Systems in Automotive Turbochargers, PhD Thesis, University of Sussex.