와류증폭기에서의 압력강하에 관한 고찰
Abstract
An analysis on pressure drop in vortex amplifier has been performed. Based on theoretical approach with flow physics on well-known firm ground from previous studies, two dimensional flow model, which is very useful to calculate pressure drop of vortex amplifier, is proposed. Parametric studies on inlet and outlet boundary conditions also have been performed so that it found the most influential parameter is the inlet swirl velocity condition. Finally, a simple formulation is given to calculate total pressure drop.
Keywords:
Ekman Number, Fluidic Devics, Pressure Drop, Vortex Amplifier, Vortex Diode키워드:
에크만수, 유동제어장치, 압력강하, 와류증폭기, 와류다이오드1. 서 론
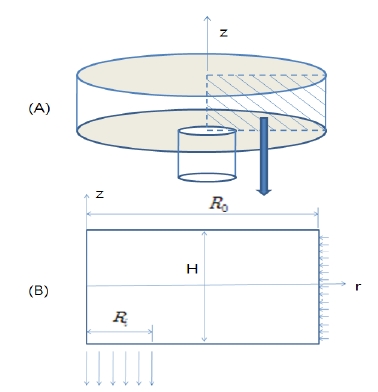
와류증폭기(vortex amplifier)는 유체가 회전할 때 발생하는 원심력 효과를 이용하여 유동저항을 증가시키는 장치이다. 와류증폭기는 Fig. 1에서와 같이 기계적으로 움직이는 부분 없이 수동적으로 작동하면서 유동방향에 따라 유동저항을 크게 혹은 작게 만들 수 있어, 마치 전기전자 회로에서 자주 사용되는 전류의 흐름을 제어하는 다이오드와 같은 효과를 발생시킬 수 있는 유동제어장치(fluidic device)로 사용된다.(1)
Fig. 1(B)에서처럼 와류증폭기의 바깥쪽 반경 r= Ro에서 반경방향속도(u)와 원주방향속도(v)를 가진 유체가 와류증폭기로 유입되면 이 유체는 반경안쪽으로 이동하면서 각운동량을 보존하기 위해 선회속도를 증가시키는 프로세스를 거치며 중심축 부근에 연결된 반경 r= Ri의 파이프를 통해 아래로 유출된다(이것은 씽크대에서 배수가 일어날 때 우리가 흔히 관찰할 수 있는 씽크유동에서 일어나는 물리현상과 유사한 유동이다). 이 과정에서 유체는 반경 r=Ro 에서 반경 r= Ri 쪽으로 이동하며 더 큰 원심력을 받게 되어 출구 쪽(반경 안쪽)으로 이동하기가 점점 힘들게 되는 유동저항을 경험하게 된다. 이후의 설명을 위해 이 유동을 정방향 유동이라 부르겠다. 유동이 앞의 설명과 반대방향으로 일어나는 역방향 유동의 경우는 상대적으로 작은 유동저항을 받게 되어 흐름이 상대적으로 원활하게 이루어진다. 따라서 와류증폭기는, 전기회로에서 전류의 양을 방향에 따라 다르게 제어하기 위해 이용하는 소자인 다이오드 같이, 흐름의 방향에 따라 유량을 제어하는 장치로 사용할 수 있다.
와류증폭기의 대표적인 사용예가 원자력발전에서 발생할 수 있는 냉각계통의 갑작스러운 사고인 냉각재 상실사고, 즉, Loss of Coolant Accident(LOCA)와 같은 비상사태에 대비하기 위한 안전장치에 사용되는 유량제어장치(Fluidic device)이다. 뿐만 아니라 와류증폭기는 흐름제어를 필요로 하는 대형수리시설, 유압회로 등에 널리 사용되고 있다.(2,3)
한 가지 언급할 것은 유동이 비록 한 방향 (정방향 혹은 역방향)으로 만 흐르는 경우를 가정해도 입구유동의 원주방향 속도를 다르게 하면 원심력효과의 크기를 조절할 수 있기 때문에 와류증폭기를 여전히 유량제어를 위한 장치로 사용할 수 있다. 사실 앞서 언급한 응용분야 대부분에서 이와 같은 형태로 사용하고 있다.
따라서 와류증폭기에서 발생하는 압력강하량에 대한 정확한 예측과 유동을 제어하기 위한 주된 설계인자를 알아보는 것은 와류증폭기 응용을 위해 중요한 연구이다.
와류증폭기에 대한 기존의 연구는 주로 1950년대부터 알려진 와류증폭기를 응용한 시스템개발에 초점이 맞추어져 있거나,(4,5) 컴퓨터를 이용한 3차원 유동해석(6) 등이 있으면 압력강하를 예측하는 이론적 모델에 대한 연구는 아직 이루어지지 않은 것으로 판단된다.
본 연구에서는 와류증폭기에서 발생하는 압력강하를 고찰하기 위해 정방향 흐름에서 발생하는 압력강하량을 예측할 수 있는 수리모형을 만들고 이를 통해 유량제어장치 설계에서 가장 중요한 설계변수가 무엇인지를 고찰하고자 한다.
2. 해석모형
Fig. 1에서와 같이 와류증폭기는 3차원 형상을 갖고 있다. 내부의 유동을 살펴보면 유동이 입구 r = Ro에서 반경 안쪽방향으로 유입되고, 이때 유입속도는 반경방향 속도 성분(u)과 회전방향 속도성분(υ)을 갖는다. 한편 대칭축부근 r ≤ Ri의 영역에서는 출구파이프를 통해 수직방향 속도성분(ω)를 발생시키며 수직으로 유출된다. 따라서 와류증폭기 내부 유동은 비점성, 축대칭 층류유동의 가정을 통해 단순화 시키더라도 u, υ, ω 속도성분을 모두 갖는 3차원 유동임을 알 수 있다.
와류증폭기 유동에 대한 자세한 정보는 3차원 Navier-Stokes 방정식에 대한 수치해석을 필요로 하지만 다음의 두 가지 가정 하에서 이론적인 접근을 통해 설계에 필요한 유용한 정보를 얻을 수 있다.
첫 번째 가정 : 에크만수가 매우 작다( E << O(1) )고 가정하면 와류증폭기 벽 근처를 제외한 나머지 유동영역 대부분에서의 유동은 비점성 유동으로 가정할 수 있다. 여기서 언급한 에크만 수는 레이놀즈 수의 역수, 즉, E = 1/Re로 회전유동 연구에서 일반적으로 사용하는 무차원 수이다.
두 번째 가정 : 와류증폭기를 흐르는 유동이 z-축 중심으로 선회하는 강한 회전유동(strongly rotating flow)이라는 점을 감안하면 대부분의 반경방향 압력강하량은 벽면 마찰보다는 회전에 의한 원심력 효과가 발생시킬 것으로 생각할 수 있다. 따라서 와류증폭기 내부유동을 비점성 축대칭 유동으로 가정하고 압력강하량을 계산하는 것은 타당한 방법이다.
Fig. 1(B)에 주어진 유동영역에 대한 해석을 보다 단순화 시킬 수 있는 한 가지 방법으로, 출구영역, 즉, 0 ≤ r ≤ Ri에서의 유동조건 변화가 입구영역 Ri ≤ r ≤ Ro에서 발생하는 유동의 압력강하량에 미치는 영향이 미미하다는 것을 보일 수 있다면(이 사실은 3장의 해석을 통해 보여줄 것이다), 두 영역에서 발생하는 압력강하량을 독립적으로 계산할 수 있다. 이후의 논의에서 0 ≤ r ≤ Ri를 출구영역, Ri ≤ r ≤ Ro를 입구영역으로 부르기로 한다. 그리고 많이 사용되는 와류증폭기의 경우 기하학적 형상이 이기 때문에 대부분의 압력강하가 입구영역에서 일어난다.
결과적으로 입구영역에서의 압력강하량에 대한 이론적인 모형을 통해 와류증폭기에서 발생하는 압력강하량을 유추할 수 있게 되면 이를 통해 응용제품에 대한 설계이론을 만들 수 있게 된다.
앞서 언급한 축대칭 층류유동 가정 하에서 입구영역(Ri ≤ r ≤ Ro)에서 발생하는 압력강하를 계산하자. E << O(1)인 경우 아래, 위판 근처의 경계층을 제외한 내부영역에서는 유동변수의 z-방향변화를 거의 무시할 수 있다. 즉, , 여기서 Φ는 u 혹은 υ이다. 이 사실은 회전유동연구 분야에서 유체가 강하게 회전하는 경우 회전축 방향으로 속도성분이 일정해지려는 경향이 있다는 Taylor-Proudman 이론으로 잘 알려져 있다.(7) 그리고 유동이 축대칭이라는 가정을 통해 유동모형은 중심축 (z-축) 방향으로 무한히 긴 중공축 실린더에서의 유동, 즉, 외측벽(r = Ro)을 통해 유체가 유입되어서 내측벽(r = Ri)을 통해 유출되는 2차원 문제로 간단히 된다. 이후의 논의에서 r = Ro을 외경, r = Ri을 내경으로 부기로 한다.
외측벽 입구 r = Ro에서 유입속도를 u = Uo, υ = Vo, 내측벽 출구 r = Ri에서의 유출속도를 u = Ui, υ = Vi라고 하자. 여기서 u는 반경방향속도, υ는 원주방향속도를 의미한다. 상기문제에 대한 2차원 원통형좌표계에 대한 축대칭 및 정상상태에 대한 지배방정식은 아래와 같은 무차원방정식으로 나타난다.(8)
| (1) |
| (2) |
| (3) |
여기서 무차원수(에크만 수)는 E=ν/UoRo이다. 무차원화를 위한 기준길이를 외경길이 R0, 기준속도를 외경에서의 유입속도의 절대값 U0, 기준압력을 이고, ν는 작동유체의 동점성계수이다.
(i) 외경에서
| (4) |
이고, (ii) 내경에서
| (5) |
이다. 무차원수 α,β,γ는 외경과 내경에서 기준속도와 반경방향 및 회전방향 속도비를 나타낸다.
3. 결과 및 토의
이제 해를 구하자. 식(1)로부터 반경방향 속도해는
| (6) |
이고, 외경(r = 1)에서의 경계조건(식 (4))를 적용하면 적분상수 C=-1.0임을 알 수 있다. 결과적으로 내경에서의 경계조건(식 (5))으로부터 γ 값이
| (7) |
이 되어야만 한다는 것을 알 수 있다. 즉, 내경의 반경방향 속도성분 u에 대한 경계조건은 질량보존을 만족시키기 위해 외경조건에 의해 종속적으로 결정된다. 결과적으로 내경에서의 반경방향 경계조건은 더미조건(dummy condition) 임을 알 수 있다.
이제 회전방향 속도성분 υ에 대한 해를 구해보자. 식 (6)의 결과를 식 (3)에 대입하면 회전방향 속도성분 υ에 대한 지배방정식을 다음과 같이 얻을 수 있다.
| (8) |
Euler 미분방정식 (8)에 대한 일반해는 다음과 같이 주어진다.
| (9) |
여기서 고유값 n1,2는 고유방정식
| (10) |
의 두 해
| (11) |
이다.
식 (9)의 미정계수 C1 과 C2는 식 (4)와 (5)에서 속도 υ에 대한 경계조건 υ (r = 1) = α, υ (r = δ) = β을 만족시키도록 다음과 같이 결정된다.
| (12) |
결과를 요약하면 회전방향 속도성분 υ의 해는
| (13) |
와 같이 나타난다.
Fig. 2를 포함한 이하의 모든 그림은 외경에서의 유입속도 u =-1.0인 경우에 대한 해석이다.
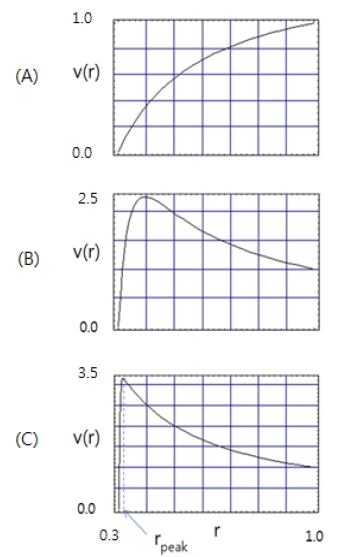
Profiles of azimuthal velocity, υ(r) when the Ekman number, E, are : (A), 1.0; (B), 0.1; (C), 0.01. (α = 1.0, β = 0.0, δ = 0.3)
Fig. 2는 외경(r=1.0)에서의 회전속도가 α = 1.0이고, 내경(r = δ = 0.3)에서의 회전속도가 β = 0.0인 경우에 대한 해를 그린 것이다. 에크만 수가 (A) E=1.0, (B) E=0.1, (C) E=0.01 이다. Fig. 2(A)의 경우 상대적으로 에크만 수가 큰 경우이기 때문에 점성효과가 전 유동영역에 걸쳐 나타난다. 따라서 υ(r)이 단조증가 분포를 보이는 것을 볼 수 있다. 이 속도분포는 극단적으로 에크만 수가 큰 경우(E→∞)에 전유동영역이 점성효과에 완전지배를 받게 되고 υ(r) 분포는 선형인 υ (r) = 10/7r - 3/7이 된다. 한편 Fig. 2(A)-(C)를 살펴보면 에크만 수가 감소함에 따라 υ(r)속도분포는 내경(r=0.3) 근처영역을 제외한 영역에서 자유와류(free vortex) 유동, 즉, υ(r) ∝ 1/r의 속도분포에 근접해 가는 것을 볼 수 있다. E= 0.01인 경우에 대한 Fig. 2(C)로부터 이 현상을 보다 자세히 관찰할 수 있다. 유동이 좁은 출구영역(0.3 ≤ r ≤ rpeak)에서는 강제와류 υ(r) ∝ r에 근접하는 속도분포를 가지고, 나머지 대부분의 유동영역(rpeak ≤ r ≤ 1.0)에서는 자유와류 υ(r) ∝ 1/r의 속도분포에 근접하는 속도분포를 가져가는 경향성을 보인다는 것이다. 그림에서 볼 수 있듯이 에크만 수가 매우 작은 경우 점성효과는 내벽근처의 매우 얇은 출구영역에만 국한되고 나머지 내부분의 영역은 비점성 운동을 하게 된다는 것을 알 수 있다. 따라서 비점성영역에서 유체의 반경방향 이동이(각운동량보존 법칙에 의해) 유체의 회전속도를 매우 크게 만들게 되고, 이때 증가된 원심력효과에 의해 유체의 반경(안쪽)방향 이동은 더 큰 압력저항에 직면한다는 사실을 알 수 있다. 정량적 측면에서 이 현상은 r = 0.3에서의 출구조건에 무관하게 r = 1.0에서 주어지는 입구유동조건에 의해 전적으로 결정된다(이 사실은 이후의 논의에서 보다 자세히 기술될 것이다). 결과적으로 E ≪ 1인 경우 출구(r = 0.3)에서의 경계조건 식 (5)는 0.3 ≤ r ≤ rpeak에 형성되는 얇은 경계층에 의해 만족되어진다는 것을 알 수 있다. E ≪ 1인 경우 경계층의 두께가 매우 얇기 때문에 이 층(0.3 ≤ r ≤ rpeak)을 가로지는 압력강하량은 내부 비점성영역(rpeak ≤ r ≤ 1.0)을 가로지르며 일어나는 압력강하량에 비해 무시할 수 있을 정도로 작다는 것을 알 수 있다.
위 사실이 2장의 해석모형 설명에서 언급했던 완전한 3차원 와류증폭기 모델에서의 압력강하량 계산을 Ri < < Ro인 경우 입구영역( Ri ≤ r ≤ Ro)에 대한 단순한 2차원모델로부터 계산할 수 있다는 주장에 대한 정당성을 부여한다.
다시 말하면, E ≪ 1이고 Ri < < Ro인 경우 유동해석을 위해 유동영역을 입구영역(Ri ≤ r ≤ Ro)과 출구영역(0 ≤ r ≤ Ri)으로 나누고, 출구영역(0 ≤ r ≤ Ri)에 대한 3차원해석을 통해 r = Ri에서의 유동조건을 계산하고 이를 다시 입구영역(Ri ≤ r ≤ Ro) 해석을 위한 r = Ri에서의 경계조건으로 사용하는 반복수치계산을 생각할 때 r = Ri에서의 경계조건이 입구영역 압력강하량에 미치는 영향이 미미하기 때문에 와류증폭기 응용시스템의 개념설계를 위한 압력강하량 계산을 위해서는 굳이 출구영역(0 ≤ r ≤ Ri) 해석을 통한 3차원해석이 필요치 않다는 이야기이다.
Fig. 3은 E = 0.05이고, 내경(r = δ(= 0.3))에서의 회전속도 υ(δ) = β를 β = 0.0로 고정시키고 외경 (r = 1.0)에서의 회전속도 υ(1) = α를 α = 1.0, 2.0, 3.0로 증가시키면서 살펴본 것이다. 그림에서 볼 수 있듯이 외경에서 유입되는 유체의 회전방향 속도성분이 클수록 내부유체의 회전속도가 α2에 비례하여 커지는 것을 볼 수 있다. 내경(r = δ(= 0.3))에서의 경계층의 두께는 α 값의 영향이 미미한 것을 볼 수 있다. 경계층의 두께는 O(E1/2)로 에크만 수에 의존하기 때문이다.
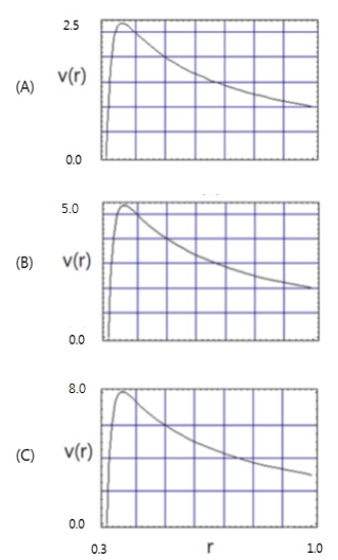
Profiles of azimuthal velocity, υ(r) when (A), α = 1.0; (B), α = 2.0; (C), α = 3.0. (β = 0.0,δ = 0.3, E = 0.05)
Fig. 4는 E = 0.05이고, 외경(r = 1.0)에서의 회전속도 υ(1) = α를 α = 0.1로 고정시키고, 내경(r = δ(= 0.3))에서의 회전속도 υ(δ)를 β = 1.0, 2.0, 3.0로 증가시키면서 해를 그린 것이다. 그림에서 볼 수 있듯이 외경에서 회전속도 증가에 따른 경계층을 제외한 영역인 내부유체의 회전속도변화는 미미하다(세로축의 척도가 달라서 Fig.4로 부터 이것을 확인하기는 다소 불편하지만 0.4 ≤ r ≤ 1.0영역에 대해 이론해를 가지고 동일척도에서 그려보면 완전히 겹치는 것을 확인할 수 있다). 내경부근의 경계층의 두께 역시 β값의 영향을 거의 받지 않는 것을 볼 수 있다.
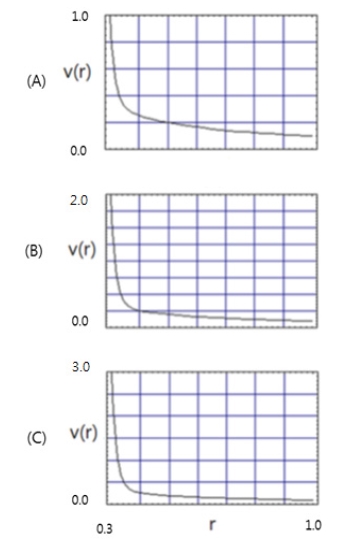
Profiles of azimuthal velocity, υ(r) when (A), β = 1.0; (B), β = 2.0; (C), β = 3.0. (α = .01,δ = 0.3, E = 0.05)
요약하면 Fig. 3 & 4로부터 경계층 영역을 제외한 내부유체의 회전속도증가에 주된 영향을 미치는 인자가 내경에서 주어지는 회전속도조건이 아니라 외경에서 유입되는 유체의 회전속도조건이라는 것을 알 수 있다. 이것은 설계적인 관점에서 주된 설계인자가 외경에서의 유입조건이라는 것을 의미한다. 이전의 연구를 살펴보더라도 많은 경우 주된 연구의 목적이 유입조건에 따른 결과에 초점이 맞추어진 사실을 확인할 수 있다. 본 연구의 결과는 이전연구의 동기 및 초점이 주로 입구조건에 맞추어져 왔는지에 대한 보다 체계적 해답을 제시한다
이제 식 (2)를 이용하여 압력강하량을 계산해보자.
| (14) |
앞서 구한 u, υ에 대한 해 식 (6), 식 (13)을 식 (14)에 대입하고 구하면 압력강하량을 구할 수 있다. 그러나 적분기호 안의 세 번째 항에 대한 해석해를 구하기는 쉽지 않고, 수치적분을 통해 구해야 한다. MATHMATICA를 이용하여 문제의 해를 구해보면 다음과 같은 흥미로운 사실을 밝혀낼 수 있다. 한 가지 언급해야할 것은 여기서 계산한 압력강하량은 점성효과를 포함한 유동 전 영역(δ ≤ r ≤ 1.0)에 대한 적분값이라는 사실이다.
Table 1은 내경과 외경사이에서 일어나는 압력강하량이 β값 변화보다는 α값 변화에 매우 의존적임을 보여준다. Table 1의 결과는 α값을 고정시키고 β값을 변화시키는 경우 압력강하량의 변화가 거의 없다. 반면 β값을 고정시키고 α 값을 변화시키는 경우 압력강하량의 변화가 매우 크다는 것을 명확히 보여준다. 이 결과는 앞서의 속도장에 대한 설명에서 언급했던 것처럼 외경(r = 1.0)에서의 입구유동조건이 대부분의 내부영역에서 유동속도에 영향을 주는 인자이고 결과적으로 이것이 압력강하량을 결정짓는 주된 요인인 반면 내경(r = δ)에서의 유동조건은 압력강하량에 미치는 영향이 미미하다는 사실은 정량적으로 다시 확인시켜준다. 이와 함께 이 결과는 2장 유동모형에서 가정한 2차원모형의 유용성에 대한 생각의 정당성을 입증해준다고 할 수 있다.

The values of total pressure drop for various inlet and outlet swirl velocities (E = 0.005, δ = 0.3)
마지막으로 언급할 사실은 점근해석법을 통한 점성효과를 포함한 완전한 3차원 모형에 대한 해석과 본 연구에서 제시한 2차원 해석의 결과는 거의 일치하는 결과를 얻었다는 것이다. 이 내용은 본 연구의 범위를 넘어서는 것으로 판단하여 본 논문에서는 다루지 않았다.
4. 결 론
와류증폭기에서 발생하는 강한 회전유동특성에 대한 이론적인 접근을 통해 유동특성을 고찰하고 이를 통해 압력강하량을 계산할 수 있는 단순화된 2차원 모형을 만들었다.
2차원 모형해석 결과를 통해 단순화 과정에 필요한 여러 가정에 일치하는 해를 얻고 이를 통해 와류증폭기의 주요 설계변수인 입, 출구유동조건에 대한 매개변수 연구(parametric study)를 수행했다. 이를 통해 에크만 수가 매우작고, 즉, E ≪ 1인 경우 와류증폭기의 출구반경(Ri)이 입구반경(Ro)보다 충분히 작으면, 즉, Ri < < Ri이면 입구영역 (Ri ≤ r ≤ Ri)에 대한 2차원 해석을 통해 와류증폭기에서의 압력강하량을 계산할 수 있다 것을 보였다.
2차원 모형으로부터 구한 이론해를 수치적분하여 압력강하량에 대한 다양한 입구 및 출구조건에 대한 정량정인 자료를 표로 제시하고 이를 통해 압력강하량에 영향을 주는 가장 중요한 변수가 와류증폭기 외경(r = Ro)에서 유입되는 원주방향속도(Vo) 임을 보이고, 출구반경(r = Ri)에서의 유동조건 변화는 압력강하량에 미치는 영향이 미미함을 보여 2차원 해석모형의 유용성을 입증했다.
Acknowledgments
본 연구는 한국연구재단의 연구지원으로 수행됨(연구과제번호 NRF-2015R1D1A1A02062408).
References
- Anderson, W. W., (1972), A Dynamic Model of Vortex-Type Fluid Amplifiers, Massachusetts Institute of Technology Ph.D. Dissertation.
- Xu, Y., Zhang, G., and Wang, F., (2011), “The Flow Simulation in the Fluidic Amplifier,”, The Open Automation and Control Systems Journal, 3, p8-12.
- Kotowski, A., and Wójtowicz, P., (2010), “Analysis of Hydraulic Parameters of Conical Vortex Regulators,”, Polish Journal of Environmental Studies, 19(4), p749-756.
- O'Brien, D., (2008), Design and Development of a Radial Vortex Flow Control Device, Dublin City University, M.S. Thesis.
- Shiraishi, T., (2011), “Design of the Advanced Accumulator for the Pressurized Water Reactor,”, Nuclear Engineering and Design, 241(9), p3910-3924.
- Lim, S. G., Lee, S. H., and Kim, H. G., (2010), “Benchmark and Parametric Study of a Passive Flow Controller(Fluidic Device) for the Development of Optimal Designs Using a CFD Code,”, Nuclear Engineering and Design, 240(5), p1139-1150.
- Greenspan, H. P., (1968), The Theory of Rotating Fluids, Cambridge University Press.
- Saffman, P. G., (1992), Vortex Dynamics, Cambridge University Press.