대형 풍력발전기용 소형 모터-발전기 시스템 설계
Abstract
Small-scale motor-generator sets have been used in laboratories for verification of real large wind turbines whose rated power are more than 1 MW. In this paper, a result of designing a small-scale motor-generator system, which is composed of motor, gear box, flywheel, and generator, is presented in the aspect of speed response. Design objective is to make a small-scale motor-generator system have the same time constant and optimal tip speed ratio region as a real MW wind turbine. A small-scale 3.5 kW motor-generator system for emulating response of a 2 MW wind turbine is considered and designed.
Keywords:
Flywheel, Motor-generator, Optimal TSR, Rotor Radius, Time Constant, Wind Turbine키워드:
플라이휠, 모터-발전기, 최적 주속비, 로터 반경, 시상수, 풍력터빈1. 서 론
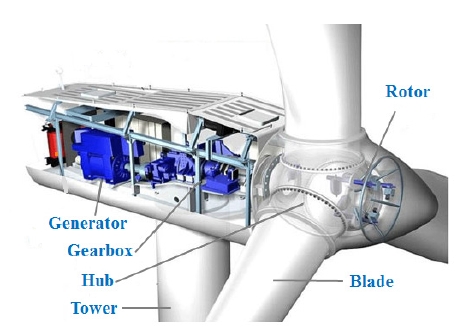
최근 지구 온난화 현상이 날로 심각해지면서 화석연료를 대체할 수 있는 신재생에너지 분야가 대두되고 있다. 그중 풍력발전기는 바람이 가진 무공해에너지로부터 블레이드를 회전시켜 기계적 에너지로 전환하여 발전기를 통해 전기를 생산하는 기계이다. 풍력발전기의 구조는 고차의 복합시스템으로써 블레이드, 허브, 기어 박스, 저속 회전축, 고속 회전축, 타워, 발전기, 피치시스템, 요시스템 등으로 구성되어 있다(Fig. 1). 최근 저비용, 고신뢰성이 미래 풍력발전기의 성공 요인으로 강조되고 있으며, 점차적으로 더 많은 출력파워를 얻기 위한 노력으로 풍력발전기의 규모가 수 MW급으로 대형화됨에 따라 안정성 확보 및 출력파워 향상을 위한 제어기의 중요성이 더욱 높아지고 있다.(1~4) 수 MW급 풍력발전기는 각 시스템 요소의 설계뿐만 아니라 고효율 출력제어 시스템을 설계하고 안정성을 확보하는 것이 매우 중요하다.
Main Components of a MW Wind Turbine System
수 MW급 풍력발전기를 실제 현장에 설치하기 전에 우선 실험실에서 출력제어 시스템의 특성과 효율을 확인하는 것이 필요하여 소형 시뮬레이터인 모터-발전기 시스템이 사용 및 연구되고 있다.(5~8) 선행 연구자들에 의해 풍력발전기의 시뮬레이터인 모터-발전기 시스템에 관한 연구가 진행되어 왔지만, 주로 전기적인 관점에서 발전기 토크제어에 대해 연구되어 왔다. 오승진 등은 Nordex사의 S70모델인 1.5 MW급 풍력발전기를 대상으로 소형 1.5 kW급 시뮬레이터를 이용한 DFIG 풍력발전시스템 하드웨어 시뮬레이터를 개발하였고, 정격풍속 이하의 영역과 정격풍속 이상의 영역에서 전력 계통 연계에 관점을 두고 발전기 회전속도에 따른 회전자 전력, 회전자 전류, 고정자 전압의 변화에 대하여 확인하였다.(5) 정병창 등은 풍력발전기 모의실험을 위해 모터-발전기 세트로 구성된 소형 3 kW급 가변 토크 입력형 시뮬레이터를 개발하였고, 정격풍속 이하의 영역에서 직류 전동기 전기자 전류와 전기자 전압의 변화에 대해 파악하고 발전기 고정자의 d-q축 전압제어와 전류제어에 대한 결과를 확인하였다.(6) 이재경 등은 1 MW급 풍력발전기 모델을 대상으로 발전기 토크제어를 위해 모터-발전기 세트로 구성된 소형 2 kW급 풍력발전기 시뮬레이터를 개발하였고, 정격풍속 이하의 영역에서 토크제어에 관점을 두었다.(7) Kwon 등은 2 MW급 풍력발전기를 대상으로 20 kW급 모터-발전기로 구성된 시뮬레이터를 개발하였고, 계통 전압과 전류를 관찰함으로써 출력파워 컨버터의 역류제어의 영향을 고찰하였다.(8)
수 MW급 풍력발전기를 대상으로 한 실험실 규모의 소형 모터-발전기 시스템의 설계에 있어서 가장 중요한 요소 중의 하나는 수 MW급 풍력발전기와 동일한 응답특성을 나타내도록 설계해야 한다는 것이다. 수 MW급 풍력발전기의 경우 블레이드의 질량 관성모멘트가 매우 커서 풍속의 변화에 대한 응답이 느리게 되어 이로 인해 출력파워에 미치는 영향이 크기 때문이다. 그러므로 실험실 규모의 소형 모터-발전기 시스템을 이용하여 발전기에서의 출력제어의 작동과 효율을 확인 시에 전기적인 측면과 함께 전체 시스템 응답의 유사성을 살펴보는 것이 필요하다. 본 논문은 이에 대한 것으로, 2 MW급 풍력발전기를 대상으로 소형 모터-발전기 시스템의 주요 파라미터들을 설계하여 응답속도 면에서 동일한 특성을 가짐을 보이고자 한다.
2. 대형 풍력발전기 모델
2.1 2MW 풍력발전기
본 논문에서 고려된 대형 풍력발전기는 2 MW급으로, 물리적인 파라미터값들은 Table 1과 같다. 로터 반경(R)은 40 m이고 기어박스의 증속비(Ngb)는 83.33이다. 2 MW 풍력발전기 모델의 정격 파라미터값들은 Table 2와 같다. 정격 로터 속도는 18 rpm이고 정격 발전기 속도는 1,500 rpm이고 정격 발전기 토크는 13.4 kNm이다.
Physical Parameter Values for the 2 MW Wind Turbine Model
Rated Parameter Values for the 2 MW Wind Turbine Model
Power Related Parameter Values for the 2 MW Wind Turbine Model
풍력발전기의 출력에 있어서 중요한 무차원 파라미터들은 주속비(⋋)와 출력계수(CP)이다. 주속비는 식 (1)과 같이 로터 허브에서의 풍속(V)과 블레이드 끝단에서의 선속도의 비로 정의되며, 출력계수는 주속비와 블레이드의 피치각(β)의 함수로 표현된다.
| (1) |
여기서 Ωr은 로터의 속도이다.
출력계수는 바람과 블레이드의 상호작용에 의해 발생하는 로터의 공력 토크와 출력에 영향을 미치는 것으로, 로터의 공력 토크(Tr)는 식 (2)와 같이 표현된다.
| (2) |
2.2. 토크 제어기
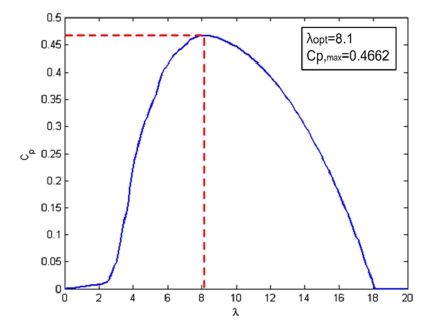
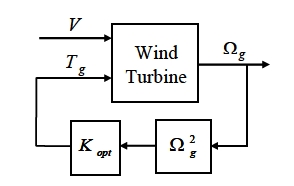
정격풍속 이하에서의 풍력발전기의 제어는 발전기의 토크 제어에 의해 수행되며 이 경우의 토크 제어의 목적은 최대의 출력파워를 생산하도록 하는 것이다. 이를 위해서는 주속비를 항상 최적값으로 유지하도록 해야 한다. 최적 주속비(⋋opt)는 출력계수가 최대값(CP,max)이 될 때의 주속비 값이다. 고려된 2 MW 풍력발전기는 정격풍속 이하에서 피치각이 0도로 유지되고 있으며, 이때 주속비에 따른 출력계수는 Fig. 2와 같다. 최적 주속비 (⋋opt는 8.1이고, 최대 출력계수 CP,max는 0.4662이다. 최적모드게인을 이용하는 토크 제어 방법은 Fig. 3에서와 같이 풍속의 크기에 따라 최적 주속비를 얻기 위하여 토크-속도의 정상상태 관계 특성을 나타내는 식 (3)을 이용하여 발전기의 토크 크기(Tg)를 발전기의 회전속도(Ωg)의 제곱에 비례하도록 제어하는 것으로 비선형제어 방법이다.(3,4,9)
Power Coefficients at Pitch Angle of 0 Degree
Torque Controller Using the Optimal Mode Gain
| (3) |
여기서 Kopt는 최적모드게인으로 발전기의 토크와 발전기의 회전속도 사이의 이차특성을 나타내는 계수값으로 식 (4)와 같다.
| (4) |
2.3 토크 제어기에 의한 응답
2 MW 풍력발전기의 로터 속도는 시동풍속에서 10.2 rpm이고 정격이상의 풍속에서 18 rpm이다. 로터 반경(R) 40 m와 최적 주속비((⋋opt) 8.1의 정보로부터 주속비 식 (1)을 이용하면 토크 제어에 의해 최적 주속비가 유지되는 풍속 구간을 구할 수 있는데, 이 경우 최적 주속비 풍속 구간은 5.3~9.3 m/s이다.
풍력발전기의 출력제어에 있어서 이 최적 주속비 풍속 구간에서의 토크 제어 특성은 매우 중요하다. 최적 주속비 풍속 구간에서는 발전기의 토크 제어에 의해 최적의 출력파워를 생산되기 때문이다. 그러므로 최적 주속비 풍속 구간에서 풍속의 변화에 따른 풍력발전기의 발전기 속도의 응답 특성을 확인해 보아야 한다.
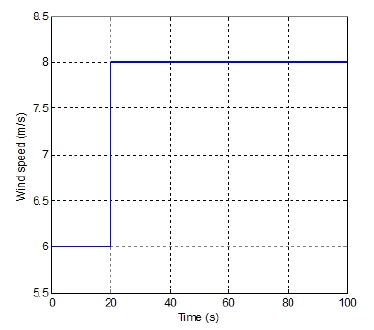
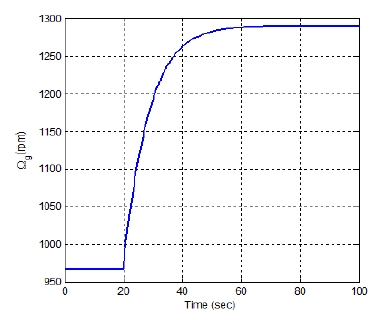
본 논문에서는 Fig. 4와 같이 최적 주속비 풍속 구간 내의 풍속 6 m/s에서 8 m/s로 변하는 계단 풍속입력을 통하여 발전기 응답 특성을 확인해 보았다. 최적모드게인을 이용하는 식 (3)의 토크 제어 방법은 비선형제어 방법이므로 풍력발전기의 모델과 토크 제어기를 통하여 발전기 속도의 응답을 해석적으로 확인하기 어려우므로 수치실험을 통하여 확인하였다. Fig. 4의 계단 풍속입력에 대한 발전기 속도 응답의 수치실험 결과는 Fig. 5와 같다. 발전기 속도의 응답은 오버슈트가 없는 1차 시스템의 특성과 비슷함을 확인할 수 있으며 풍속의 변화에 대하여 반응하는 응답 속도가 매우 느림을 확인할 수 있다. Fig. 5로부터 2 MW 풍력발전기의 응답 성능은 시상수는 8.6초, 상승시간은 17.9초, 정착시간은 31.2초임을 확인하였다. 2 MW 풍력발전기의 응답이 느린 이유는 블레이드의 길이가 40 m로 매우 길어 블레이드에 의한 로터의 질량 관성모멘트가 매우 크고, 또한 최적모드게인을 이용한 토크 제어기는 발전기의 토크 크기를 빠르게 조절할 수 없기 때문이다.
Step Input of Wind Speed
Generator Speed of the 2MW Wind Turbine
3. 소형 모터-발전기 시스템
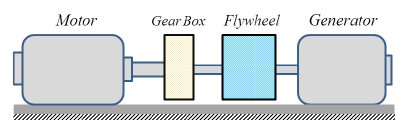
3.1 3.5 kW 소형 모터-발전기 시스템의 구성
2 MW 풍력발전기의 발전기 속도의 느린 응답 특성(시상수 8.6초 등)을 동일하게 나타내는 시뮬레이터인 3.5 kW 소형 모터-발전기 시스템을 설계하고자 한다. 3.5 kW 소형 모터-발전기 시스템은 모터, 기어박스, 플라이휠, 발전기로 크게 구성된다. 모터는 바람과 블레이드의 상호작용에 의해 발생하는 공력토크를 구현하기 위한 것이고, 발전기는 풍력발전기의 토크 제어를 구현하기 위한 것이다. 특히, 기어박스와 플라이휠은 모터-발전기 시스템의 응답속도와 관련이 있는 것으로, 이를 사용하지 않으면 모터-발전기 시스템의 응답속도는 매우 빨라 2 MW 풍력발전기의 느린 응답속도와 동일한 특성을 표현할 수 없으므로 중요한 구성 요소이다.
A Small-Scale Motor-Generator System
3.2 설계 목적 및 성능
3.5 kW 소형 모터-발전기 시스템의 설계 목적은 고려된 실제 2 MW 풍력발전기와 발전기의 응답속도 면에서 동일한 특성을 가지도록 설계하는 것이다. 설계를 통해 만족해야 할 소형 모터-발전기 시스템의 성능은 발전기 속도의 시상수 8.6초와 최적 주속비 풍속 구간 5.3~9.3 m/s로, 이는 2 MW 풍력발전기와 동일한 성능임을 말해 준다. 3.5 kW 소형 모터-발전기 시스템을 통하여 2 MW 풍력발전기의 출력제어를 모사하기 위해서 출력계수(CP)는 2 MW 풍력발전기와 동일하게 사용하였다.
3.3 설계 파라미터들의 종류
3.5 kW 소형 모터-발전기 시스템의 설계 파라미터들은 로터 반경(Rs), 기어박스의 증속비(Ngbs), 플라이휠의 질량 관성모멘트(Jfω)이다. 모터를 통하여 바람과 블레이드의 상호작용에 의해 발생하는 공력 토크를 구현하기 위하여 로터 반경의 선정이 필요하다. 로터 반경은 식 (2)와 식 (4)에서 확인할 수 있는 것처럼 공력 토크뿐만 아니라 최적모드게인의 값에도 영향을 주는 파라미터이다. 기어박스의 증속비와 플라이휠의 질량 관성모멘트는 발전기 속도의 응답을 느리게 조절하기 위해 필요한 것으로 전체 시스템의 등가 질량 관성모멘트에 영향을 주는 파라미터이다. 기어박스의 증속비는 또한 식 (4)에서 확인할 수 있는 것처럼 최적모드게인의 값에도 영향을 주는 파라미터이다.
3.4 설계 파라미터들의 선정
정격 출력이 3.5 kW인 소형 모터-발전기 시스템의 설계 파라미터들을 선정하기 위하여 우선 국내와 국외의 3 kW급 소형 풍력발전기 업체들의 제품을 조사해 보았다. 3 kW급 소형 풍력발전기의 실제 블레이드 길이는 약 2~2.5 m 범위에 있었고 정격 로터속도는 약 220~440 rpm 범위에 있음을 확인하였다. 이를 바탕으로 3.5 kW인 소형 모터-발전기 시스템의 설계 파라미터들을 선정하기 위한 기초 자료로 활용하였다.
우선 기어박스의 증속비를 선정하기 위하여 감속기 업체들의 사양을 확인하였다. 감속기의 동력이 3.7 kW인 경우 다양한 감속비(1/5, 1/10, 1/15, 1/20, 1/30 등)에 대하여 정격 출력속도를 확인하였는데, 감속비가 5인 경우 정격 출력속도가 350 rpm이었고 감속비가 10인 경우 정격 출력속도가 175 rpm이었다. 이를 바탕으로 감속비가 5인 기어박스를 사용하기로 결정하였다. 그러므로 3.5 kW 소형 모터-발전기 시스템에서 기어박스의 증속비를 5로 선정하였고, 기어박스의 입력이 되는 로터의 정격 속도는 350 rpm이고 출력이 되는 발전기의 정격 속도는 1,750 rpm으로 선정하였다.
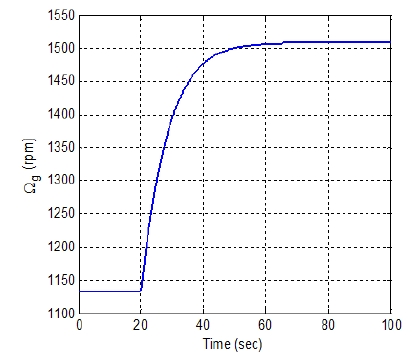
다음으로 로터 반경(Rs)과 플라이휠의 질량 관성모멘트(Jfω)를 선정하였는데, 이들 두 파라미터들은 발전기의 응답속도를 확인함을 통하여 선정할 수 있다. 이를 위하여 3.5 kW 소형 모터-발전기 시스템에 식 (3)과 같이 최적모드게인을 이용하는 토크 제어 방법을 적용하여 발전기의 응답 성능을 확인하였다. 2 MW 풍력발전기의 경우처럼 Fig. 4와 같이 풍속 6 m/s에서 8 m/s로 변하는 계단 풍속입력을 통하여 발전기 응답특성을 확인해 보았다. 수치실험 결과 로터 반경은 2 m 정도가 적당함을 알 수 있었고, 로터 반경이 1.9~2.1 m 사이에서 시상수가 8.6초가 되는 플라이휠의 질량 관성모멘트를 구할 수 있었다. Table 4는 그 결과를 보여준다. 시상수를 8.6초로 동일하게 만들기 위해서는 로터 반경이 길어질수록 플라이휠의 질량 관성모멘트가 커져야함을 확인할 수 있다. 또한 로터 반경(Rs)과 최적 주속비(⋋opt)의 정보로부터 주속비 식 (1)을 이용하면 토크 제어에 의해 최적 주속비가 유지되는 풍속 구간을 구할 수 있는데, 로터 반경이 길어질수록 최적 주속비 풍속 구간의 시작점과 끝점이 커짐을 확인할 수 있다. 이와 같은 확인 절차를 통하여 2 MW 풍력발전기와 동일한 성능인 시상수 8.6초와 최적 주속비 풍속 구간은 5.3 ~ 9.3 m/s를 동시에 만족하는 소형 모터-발전기 시스템의 로터 반경(Rs)은 2.05 m로 플라이휠의 질량 관성모멘트(Jfω)는 1.77 kgm2로 선정할 수 있었다. 선정된 값들을 이용했을 때의 계단 풍속에 대한 발전기 속도의 응답은 Fig. 7과 같다. Fig. 7로부터 설계된 3.5 kW 소형 모터-발전기 시스템의 응답 성능은 시상수는 8.6초, 상승시간은 17.9초, 정착시간은 31.2초로 적용 대상인 2 MW 풍력발전기의 응답 성능과 동일함을 확인할 수 있었다.
Time Constants and Optimal Tip Speed Ratio Regions for the 3.5kW Motor-Generator System
Generator Speed of the 3.5 kW Motor-Generator System
4. 결 론
본 연구에서는 수 MW급 풍력발전기와 동일한 응답특성을 나타내는 소형 모터-발전기 시스템의 설계에 관하여 살펴보았는데, 최적모드게인을 이용하는 토크 제어 방법을 적용하여 발전기의 응답 성능을 확인함을 통하여 설계 파라미터들을 선정할 수 있음을 보였다.
우선 2 MW 풍력발전기를 대상으로 최적모드게인을 이용하는 토크 제어 방법을 적용하였을 때의 응답 성능을 확인하였다. 최적주속비 풍속 구간은 5.3~9.3 m/s임을 확인하였고, 이 구간에서 계단 풍속에 대한 발전기 속도 응답을 구하였다. 발전기 속도의 응답은 오버슈트가 없는 1차 시스템의 응답 특성과 비슷함을 확인하였고, 이를 바탕으로 응답 성능이 되는 시상수가 8.6초로 매우 느린 응답 특성을 가짐을 확인하였다.
다음으로 2 MW 풍력발전기와 동일한 최적주속비 풍속 구간과 시상수를 가지도록 3.5 kW 소형 모터-발전기 시스템을 설계하였는데, 이때 출력제어 모사를 위하여 출력계수는 2 MW와 동일한 자료를 사용하였다. 최적모드게인을 이용하는 토크 제어 방법을 적용하여 발전기의 응답 성능을 확인함을 통하여, 기어박스의 증속비는 5이고 로터 반경은 2.05 m이고 플라이휠의 질량 관성모멘트는 1.77 kgm2으로 선정하였다. 이와 같이 설계된 3.5 kW 소형 모터-발전기 시스템은 최적주속비 풍속 구간은 5.3~9.3 m/s이고 시상수가 8.6초로 2 MW 풍력발전기와 동일한 응답 성능을 보임을 확인하였다.
Acknowledgments
본 연구는 한밭대학교 2014년도 교내학술연구비의 지원을 받아 수행한 연구 결과입니다.
References
- Hansen, A. D., and Hansen, L. H., (2007), “Wind Turbine Concept Market Penetration over 10 Years,”, Wind Energy, 10(1), p81-97.
- Joselin Herberta, G. M., Iniyanb, S., Sreevalsanc, E., and Rajapandian, S., (2007), “A Review of Wind Energy Technologies”, Renewable and Sustainable Energy Reviews, 11(6), p1117-1145.
- Bossanyi, E. A., (2000), “The Design of Closed-loop Controllers for Wind Turbines”, Wind Energy, 3(3), p149-163.
-
Burton, T., Sharpe, D., Jenkins, N., and Bossanyi, E., (2001), , “Wind Energy Handbook,”, John Wiley & Sons, Ltd.
[https://doi.org/10.1002/0470846062]
- Oh, S. J., Cha, M. Y., Kim, J. W., Jeong, J. K., Han, B. M., and Chang, B. H., (2011), “Development of Hardware Simulator for DFIG Wind Power System Composed of Anemometer and Motor-Generator Set,”, The Transactions of Korean Institute of Power Electronics, 16(1), p11-19.
- Jeong, B. C., Song, S. H., Rho, D. H., and Kim, D. Y., (2002), “A Wind Turbine Simulator with Variable Torque Input,”, The Transactions of the Korean Institute of Electrical Engineers, 51B(8), p467-474.
- Lee, J. K., Park, J. Y., Oh, K. Y., and Park, J. S., (2011), “Development of Wind Turbine Simulator for Generator Torque Control,”, International Journal of Mechanical, Aerospace, Industrial, Mechatronic and Manufacturing Engineering, 5(10), p1965-1968.
- Kwon, S. J., Son, Y. G., Jang, S. D., Suh, J. H., Oh, J. S., Chun, C. H., Chung, C. W., Han, K. S., Kim, D. H., and Kwon, O. J., (2006), , “A Simulator for the Development of Power Conversion System for 2 MW Wind Turbine,” European Wind energy Conference and Exhibition, Athens, Greece.
- Lim, C. W., (2013), “Dynamic Response of a 2.75 MW Wind Turbine Applying Torque Control Method Based on Torque-Mode,”, The KSFM Journal of Fluid Machinery, 16(6), p5-11.