The Effect of Pump Intake Leaning Angle and Flow Rate on the Internal Flow of Pump Sump

2.1 Pump intake model

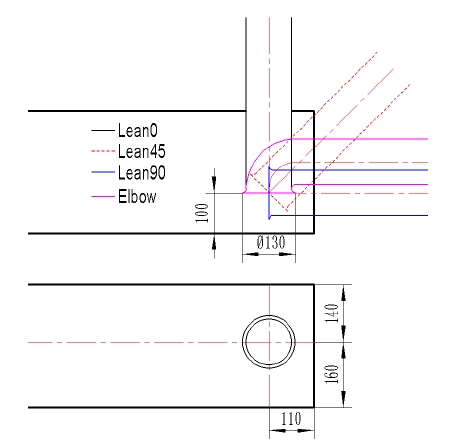
Fig. 1 shows the 2-D view of the pump sump model with different suction pipe types. The pump sump model of TSJ (Turbomachinery Society of Japan)⁽⁵⁾ was selected for investigating the effect of suction pipe leaning angle on the pump sump internal flow.

Fig. 1

2-D view of the pump sump model with different pump intake pipe types

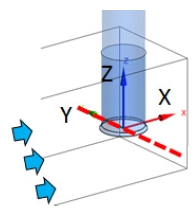
The diameter of the pump intake is D=130 mm. the distance between the inlet bell and floor is C=100 mm. The distance from the rear wall to the pump inlet bell centerline is B=110 mm. The pump inlet bay entrance width is W=300 mm. However, the suction pipe center location is eccentric distribution at the width direction of the pump sump as shown in Fig. 1.

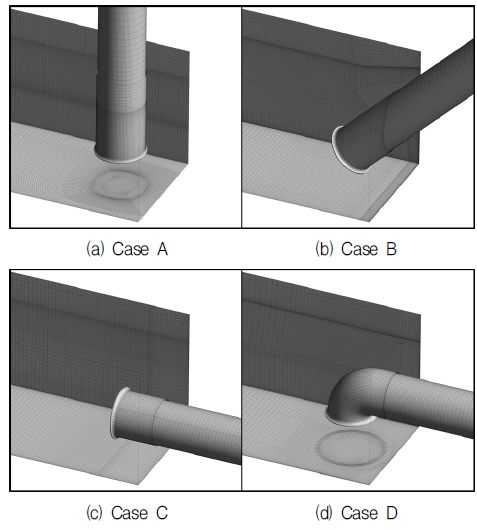
There are 3 leaning angles for the pump intake pipe. The leaning angle of 0˚ is vertical pipe type for Case A. The leaning angle of 45˚ is made for Case B. The pump intake pipe is horizontal arrangement for Case C, for which leaning angle is 90˚. Moreover, there is a pump intake pipe with elbow type as Case D. The pump intake pipe inlet center is kept same for all of cases as shown in Fig. 1. In addition, there are four different outflow rate from Q=0.5 m³/s to Q=1.5 m³/s, applied to different pump intake pipe types as shown in Table 1.

Table 1

Cases with different flow rate and pump intake pipe types

2.2 Numerical methods

2.2.1 Numerical boundary condition and meshes

For the processing of numerical simulation, a commercial CFD code of ANSYS CFX⁽⁶⁾ is adopted. Matsui et al.⁽⁷⁾, studied about the numerical simulation on the flow in pump sump with free surface with tetrahedral and hexahedral numerical mesh. According to their study, the tetrahedral numerical mesh can not simulate a smooth water surface. Therefore, the hexahedral numerical meshes of the flow field is applied for each case as shown in Fig. 2. The elements of around 1.3×10⁶ are employed to mesh the fluid domain.

Fig. 2

Local view of fine hexahedron numerical mesh

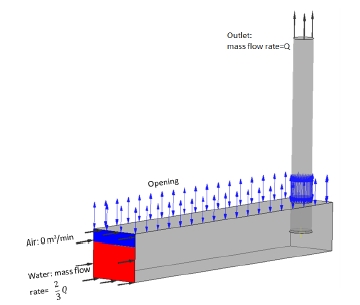
As boundary conditions for the unsteady state calculation the mass flow rate of Q (Table 1) is set for the water flow at the outlet. In order to gradually reduce the water level by the time, the water mass flow rate of $$ \frac{2}{3}Q$$ and air mass flow rate of 0 are set at inlet. The boundary condition of opening is set at the open duct. The no-slip condition is applied to all of the walls as shown in Fig. 3. Gravity is included for two phase transient calculation. The unsteady state simulation is started from the result of steady state calculation. SST (Shear Stress Transport) turbulence model is used to realize the complicated vortex flow around the pump sump in detail. SST model is two equation turbulence model by Menter et al.⁽⁸⁾. Therefore, the turbulence model of SST is adopted in this study.

Fig. 3

Boundary condition for the numerical analysis

2.2.2 Validation test of present CFD analysis method

The CFD method is very important for investigating the flow analysis. The bench marking study for the determined shape of a single pump intake was conducted to acquire the reliability of present CFD analysis method.

The pump sump model of TSJ was selected for the bench marking simulation. Fig. 4 shows the dimension of the TSJ pump sump model. In order to get vortices generated steadily, the center oof pump intake was set no on the centerline of sump.⁽⁵⁾ The unsteady state calculation was conducted for the validation test of present CFD analysis method after the 3D modeling and the numerical mesh was established. Table 2 shows the characteristics of CFD codes contributing to establishment of benchmark.

Fig. 4

TSJ model for validation test(5)

Table 2

Characteristics of CFD codes contributing to establishment of benchmark(5)

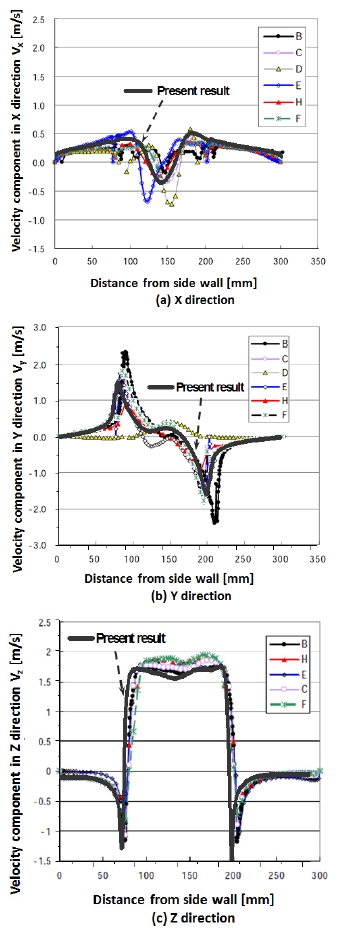
The comparison of present result with the benchmark CFD result is shown in Fig. 5. The comparison result reveals that the velocity component distribution in X, Y and Z directions of present result agrees well with the CFD results by other contributed CFD codes. There is reverse flow in the suction pipe center. The negative velocity occurs at the velocity component in X direction (Vx). The eccentrical whirling flow according to the eccentricity of the suction pipe location is found as shown in Fig. 5 (b).

Fig. 5

Comparison of present result with benchmark CFD results

3.1 Vortex classification

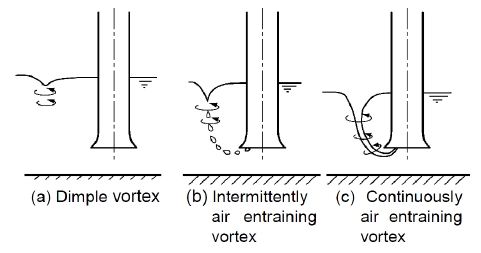
The acceptance criteria of TSJ was applied to estimate the effect of the pump intake leaning angle and flow rate on the internal flow characteristics of pump sump. There are three classification of vortices was applied as shown in Fig. 6.

Fig. 6

Vortex classification

For the vortex type of class a, Fig. 6 (a), only the dimple vortices are allowed. The surface dimple vortex occurs at the water air interface near suction pipe. For the vortex type of class b, Fig. 6 (b), the dimple vortices and intermittent vortices occurring twice a observing time are allowed. For the vortex type of class c, Fig. 6(c), the dimple vortices and intermittent vortices are allowed. In order to estimate the effect of pump intake leaning angle and flow rate on the internal flow of pump sump, those three acceptance criteria are used.

The water level (H) is the height between water air interface and tank floor as shown in Fig. 7. Fig. 8 is shown the results with three criteria. The velocity (v_s) at the abscissa is the velocity in the suction pipe, for which definition is shown as follow:

Fig. 7

Definition of the water level height (H)

Fig. 8

Three classification region of velocity and water level

where, the Q is the outflow rate and the unit of the Q is m³/min.

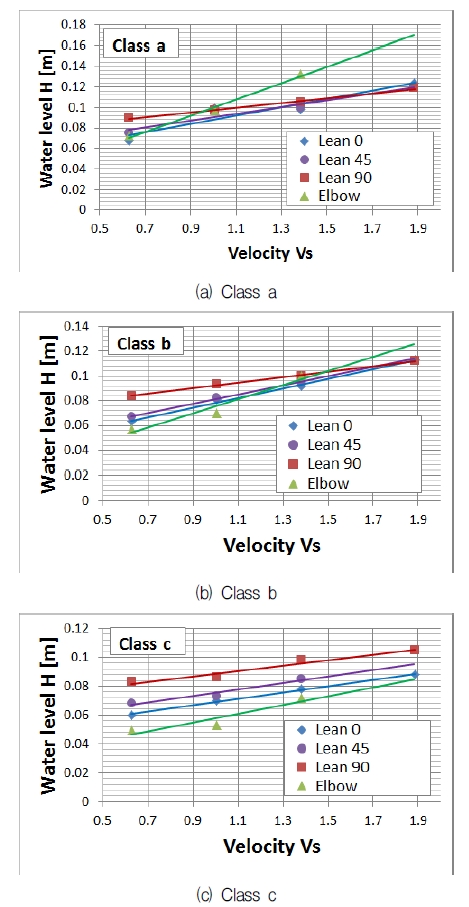
Fig. 8(a) is the relationship between water level height and velocity (Vs) at the condition of the Class a vortex occurring. The water level of elbow pump intake type increases rapidly with increasing the velocity, which means that the pump intake of elbow type easily occurs the Class a vortex in comparison to other pump intake type at high velocity (flow rate) condition.

Fig. 8(b) is the relationship between water level height and velocity (Vs) at the condition of the Class b vortex occurring. The pump intake with large leaning angle easily occurs vortex of Class b at the lowe velocity (flow rate). However, even though the pump intake type is different, there is similar water level when the velocity achieve or larger 1.4 m²/s.

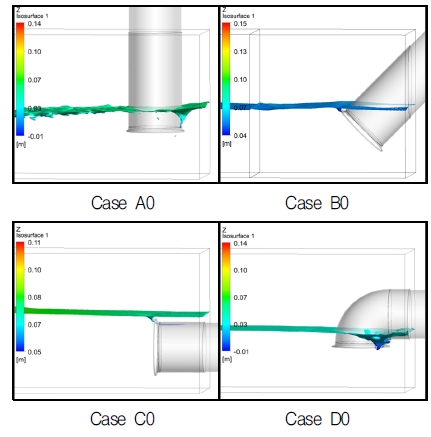
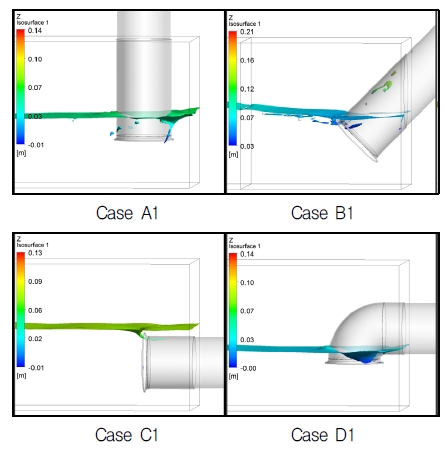
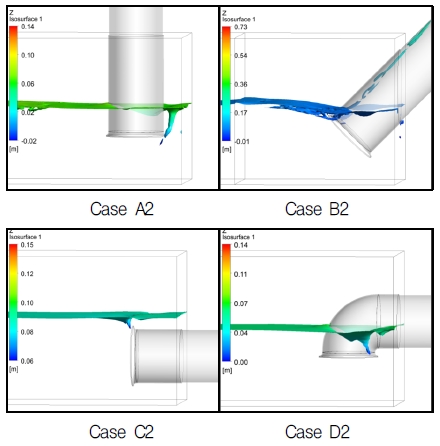
Fig. 8(c) is the relationship between water level height and velocity (Vs) at the condition of the Class c vortex occurring. There is obviously water level by different leaning angle and velocity. With increasing the velocity (flow rate), the slope of the different pump intake type is similar distribution. The water level of large leaning is high, and that of elbow type is the lowest, which means that the large leaning pump intake pipe has the highest risk to occur air entrainment and the elbow type is the safest one.

3.2 Free surface analysis

The visualization of free surface is a very important factor to examine the free surface vortex. Moreover, the vortex of Class c has the highest risk for the pump sump system. Therefore, the elevation of free surface with Class c vortex are presented in Figs. 9 to 11. The surface is visualized as a position whose water volume fraction is 0.7. As the water surface keeps moving in the simulation, this is a snapshot at a certain time, which time step is typically for the internal flow analysis.

Fig. 9 to 11 are the free surface flow shape with vortex of Class c at the flow rate from 0.5 m³/s to 1.1 m³/s by the pump intake pipe type, respectively. It can be seen that there is obviously air entrainment near the bell mouth at each case. Moreover, the water level increases with increasing the flow rate from Fig. 9 to 11.

Fig. 9

Free surface flow shape with Class c at Q=0.5 m3/s

Fig. 10

Free surface flow shape with Class c at Q=0.8 m3/s

Fig. 11

Free surface flow shape with Class c at Q=1.1 m3/s

3.3 Velocity component analysis

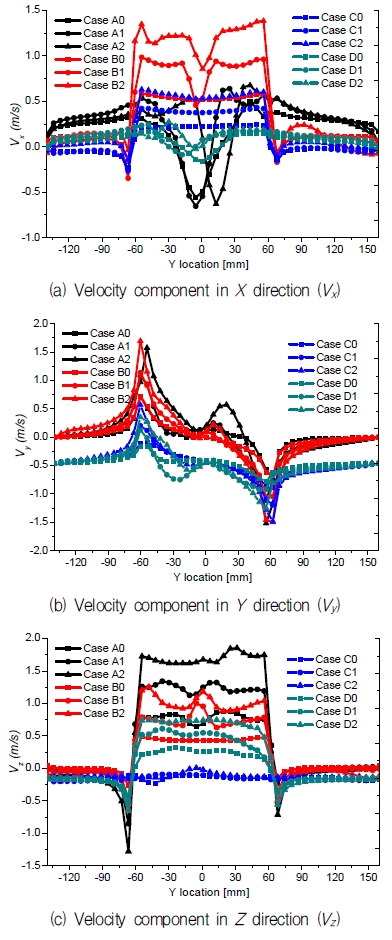
For the purpose of examining the effect of the pump intake leaning angle and flow rate on the pump sump internal flow characteristics in detail, quantitative value of the velocity components distribution at the pump intake is investigated. The vortex of Class c is selected for the velocity component analysis. The measuring location of velocity component is shown in Fig. 12. The coordinate is located at the center of the pump intake. The 0 of the abscissa is the center of the pump intake. The velocity components located on Y axis are plotted in Fig. 13.

Fig. 12

The measurement location of velocity

Fig. 13

Velocity component distribution

Fig. 13(a) shows the velocity component distribution in X direction (Vx). As the bell mouth of Case A and D is vertical, the Vx of those two cases has similar tendency. However, the Vx of Case A has large negative velocity at the center of the bell mouth. Furthermore, there is the highest Vx exists for the pump sump with 45˚ leaning angle pump intake.

Fig. 13(b) presents the velocity component distribution in Y direction (Vy). The Vy of pump sump with 0˚ and 45˚ leaning angle has similar distribution. Moreover, that with 90˚ leaning angle and elbow type has the similar distribution. In general, the Vy of the pump sump with leaning angle smaller than 45˚ is high in comparison to other cases.

Fig. 13(c) indicates the velocity component distribution in Z direction (Vz). There is almost no Vz of the pump sump with 90˚ leaning angle. The velocity component has similar tendency in Z direction by different pump intake type and flow rate.