프란시스 수차 축소 모델의 수력학적 성능 특성에 대한 형상 매개변수 연구

2.1 프란시스 수차 사양

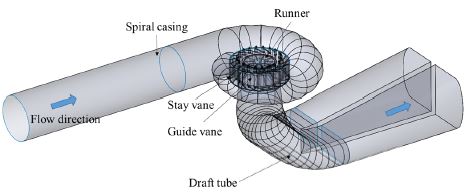
이전 연구에서 유동해석이 수행된 실물 프란시스 수차를 해당연구의 기본모델로 선정하여 상사를 수행하였으며, 직경 0.32m로 상사된 프란시스 수차 모델에 대하여 삼차원 수치해석을 수행하였다.⁽⁷⁾ Fig. 1에 본 연구 모델인 프란시스 수차 축소 모델 러너 등 주요 유동 영역에 대한 삼차원 형상을 도시하였다. 주요 제원은 Table 1에 나타냈으며, 프란시스 수차의 비속도는 식 (1)을 사용하여 나타내었다. 실물 프란시스 수차 및 모델의 회전속도, 낙차 및 유량은 IEC 60193 규격의 계수인 식 (2)~(4)를 사용하여 나타내었고, 정격운전조건을 토대로 가이드 베인 간극 및 프란시스 수차의 표면 조도에 따른 내부 유동 특성을 분석하였다.

Fig. 1

3D modeling view of a Francis hydro turbine

Table 1

Design specifications of a Francis hydro turbine

여기서, n, P, H, g, D 및 Q는 각각 회전속도, 출력, 낙차, 중력가속도, 수차의 대표직경 및 유량을 나타낸다.

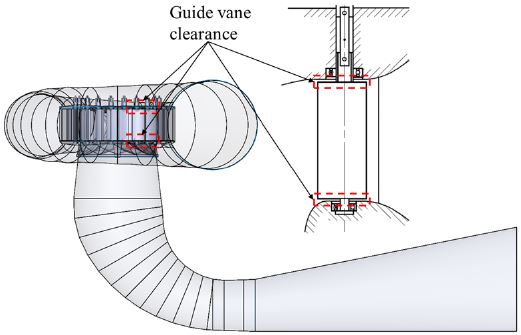
Fig. 2는 프란시스 수차 축소 모델 내 가이드 베인 간극의 위치와 IEC 60193에서 나타낸 형상을 도식화 하고 있다.⁽³⁾ Fig. 2에 나타난 바와 같이 가이드 베인 끝단에 위치한 간극은 가이드 베인 토크 측정 시 가이드 베인과 벽면의 마찰 손실을 최소로 하여 정확한 토크를 측정하기 위한 역할을 한다. 프란시스 수차 축소 모델의 가이드 베인 높이는 약 127mm이고, 가이드 베인 간극에 따른 성능 및 내부유동특성 분석을 위해 간극이 없는 모델을 기준으로 하여 0.3mm, 0.5mm 및 1mm 간극에 대해 해석을 수행하였다.

Fig. 2

Locations of guide vane clearance in 3D modeling and guide vane for torque measurement(3)

프란시스 수차의 표면 조도에 대한 규격은 IEC 60193에 제시되어 있다.⁽³⁾ Table 2에 기술된 Case 1은 IEC 60193에서 제시된 반동수차의 각 구성요소에 대한 표면조도의 최대값이며, Case 2는 표면조도에 대한 영향을 분석하기 위해 규격에 제시된 최대값의 2배를 적용하여 비교분석하였다.

Table 2

Surface roughness definition of a Francis hydro turbine model

표면조도의 적용은 벽면 근처의 난류 발생의 증가로 이어지고, 결과적으로 벽 전단응력이 증가하게 된다. 이와 같은 표면조도에 대한 벽면 근처 유동의 정확한 예측을 위해, ANSYS CFX-Pre 내 프란시스 수차의 각 구성요소 표면에 대해 식 (5) 및 (6)이 적용된 Sand Grain Roughness를 사용하여 해석을 수행하였다.⁽⁸⁾

여기서, u⁺는 벽 근처 속도 나타내고, k는 카르만 상수 및 y⁺는 벽면으로부터 무차원 거리를 나타낸다. ΔB는 무차원 표면조도 높이의 함수를 나타내며, h_s는 표면조도 평균 높이를 나타낸다.

2.2. 수치해석기법

본 연구에서는 ANSYS 사의 상용 소프트웨어인 ANSYS CFX-17.1을 사용하여 해석을 수행하였다.⁽⁸⁾ 프란시스 수차 축소 모델의 내부유동 특성은 삼차원 비압축성 RANS 방정식에 의해 유동해석이 수행되었고, 수치해석 시 계산에 사용된 지배방정식은 유한체적법으로 이산화되었다. 유동해석을 위한 난류모델로는 Shrear Stress Transport (SST) 모델을 사용하였으며, 이 모델은 유동박리 등의 예측에 적절하며, 자유 흐름 영역 뿐만 아니라 벽면 인근 영역 해석에 정확성을 보이는 모델로서 다른 2-방정식 난류모델들에 비해 유체기계해석에 적절한 모델이다.^(9~10)

프란시스 수차 축소 모델 해석을 위한 형상의 정의, 격자생성, 경계조건의 정의, 유동해석 및 결과분석은 각각 Blade-Gen, Turbo-Grid, CFX-Pre, CFX-Solver 및 CFX-Post를 사용하였으며, 작동유체는 25℃의 물로 설정하였다. 경계조건으로는 입구에 균일한 상태의 전압력을 부여하고, 출구에는 정압력 조건을 주었다.

수치해석 모델인 프란시스 수차 축소 모델에 대해 동일한 낙차 조건과 여러 가이드 베인 간극 및 표면 조도를 적용하여 해석을 수행하였다. 대부분 축 방향으로 회전하는 유체기계는 계산 시간의 단축 및 수렴성 향상을 위해 하나의 유로에 대해 주기조건(periodic condition)을 부여하여 날개 1매의 유동영역을 해석도메인으로 설정하지만, 본 연구의 해석 모델인 프란시스 수차는 확장되어지는 유동 단면을 가진 스파이럴 케이싱과 스테이 베인 사이에서 발생하는 내부 유동의 상호작용에 의해 주기적이라 가정될 수 없기 때문에 러너 등 모든 블레이드를 포함한 전 영역에 대해 해석을 수행하였다.

Fig. 3은 프란시스 수차 축소 모델의 격자계 구성을 보여주고 있다. 전체영역은 육면체 격자로 이루어 졌으며, 러너, 스테이 베인 및 가이드 베인의 날개표면 인근에는 O형 격자계를 구성하고, 그 외 스파이럴 케이싱 및 드래프트 튜브는 H/J/C/L형 격자계로 구성하였다. 수치해석 시 벽 근처 영역에서는 저 레이놀즈수 전단이송모델을 적용하기 위해 첫 번째 격자점에서 y+≤2를 유지하도록 하였다. 최적의 격자계 구성을 위한 격자의존성 테스트는 이전의 연구에서 수행된 결과를 토대로 프란시스 수차 모델 전 영역에 대한 격자 수는 총 810만개로 구성되었다.⁽⁷⁾

Fig. 3

Numerical grid of a Francis hydro turbine model

3.1 수치해석결과의 검증

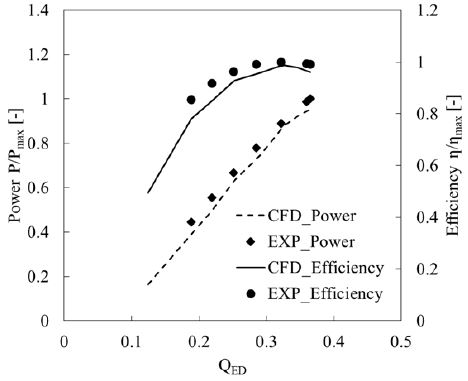
본 연구대상인 프란시스 수차의 수치해석을 수행하기 위하여 성능시험결과와의 비교를 통한 수치해석결과의 검증은 Kim 등⁽⁷⁾으로부터 수행된 선행연구에 의해 타당성이 기 입증된 바 있다. Fig. 4는 선행연구로부터 수행된 정상상태의 RANS 해석결과와 성능시험의 결과를 비교하고 있다. 수치해석의 출력 및 효율 계산은 각각 식 (7) 및 (8)을 사용하였다.

Fig. 4

Validation test of the numerical analysis

여기서, T, ω 및 ρ는 각각 러너의 토크, 각속도 및 물의 밀도를 나타내며, 그 외 기호의 의미는 위의 식 (1)~(4)와 동일하다.

Fig. 4에서 볼 수 있는 바와 같이 수치해석결과와 성능시험결과가 전반적으로 경향이 잘 일치하는 것을 볼 수 있으며, 특히 최대효율지점에서 예측한 성능의 경향이 비교적 정확하기 때문에 수치계산의 타당성이 있다고 볼 수 있다.

3.2 가이드 베인 간극에 따른 성능 특성 비교

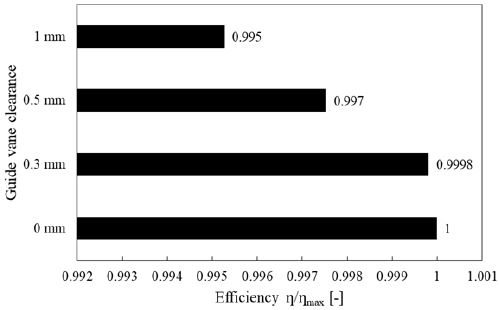
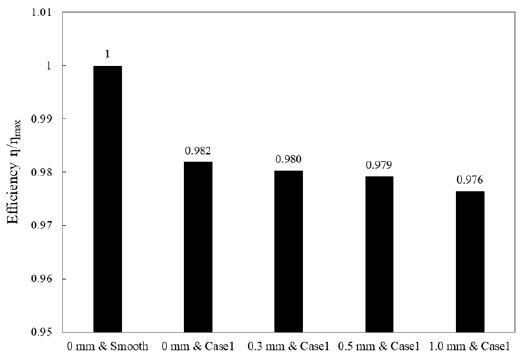
본 연구에서는 정격운전 조건에서 정상상태의 삼차원 해석을 수행하여 Fig. 5와 같이 가이드 베인 간극에 따른 효율 비교를 통해 프란시스 수차 축소 모델의 가이드 베인 간극에 따른 수력학적 성능에 대하여 살펴보았다. 효율값은 최대 효율로 나누어 무차원화 하였고, Fig. 5에서 보는 바와 같이 가이드 베인 간극이 증가함에 따라 효율은 상대적으로 감소하는 경향을 볼 수 있다. 특히, 가이드 베인 간극에 따라 감소되는 효율 폭이 최대 0.5%까지 차이가 나는 것을 확인할 수 있는데, 이는 축소 모델 제작 시 고려해야할 형상 매개변수임을 잘 설명하여 주고 있다.

Fig. 5

Efficiency comparison of a Francis hydro turbine model with various guide vane clearance

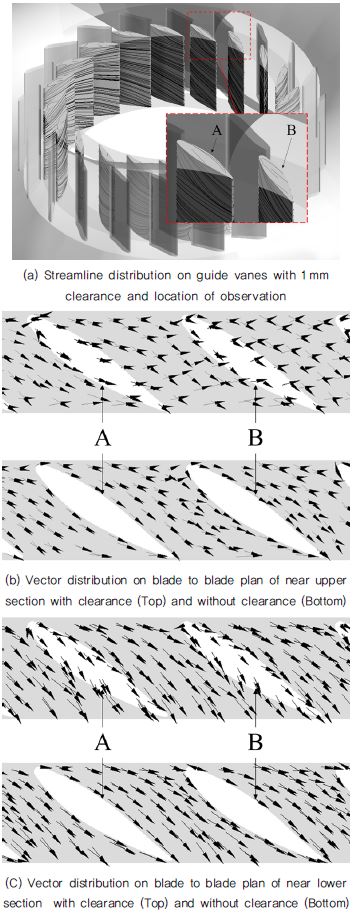
가이드 베인 간극에 따른 가이드 베인의 내부 유동 특성을 확인하기 위해 Fig. 6에 프란시스 수차 축소 모델의 가이드 베인 간극 1mm에 대한 유선분포와 가이드 베인 상단 및 하단부에 대해 간극 유무에 따른 속도 벡터 분포를 나타내었다. Fig. 6(a)에서도 확인할 수 있듯이 간극 1 mm가 적용된 가이드 베인 상단부에서 유선분포를 통해 누설 유동이 발생하는 것을 확인 할 수 있다. Fig. 6(b) 및 (c)에서는 Fig. 6(a)에서 나타낸 스파이럴 케이싱 설부(tongue) 인근 두 개의 가이드 베인 사이 유로의 상단 및 하단부 평면에서의 속도 벡터 분포를 보여주고 있다. 가이드 베인 간극이 없는 상단과 하단부 평면의 속도 벡터 분포는 가이드 베인을 따라 부드러운 흐름을 보이고 있는 반면, 상⋅하단부 가이드 베인 간극의 중간단면에서의 속도 벡터 분포는 양쪽 간극 모두에서 다소 불규칙한 누설 유동을 보이고 있다. 이러한 간극의 누설 유동은 러너의 유입 유동에 부정적인 영향을 주어 결국 수력학적 성능 감소에 원인이 되며, Fig. 5의 효율 비교에서 간극 0.3 mm 대비 0.5 mm 및 1 mm에서 효율이 상대적으로 급격히 감소하는 특성은 간극의 증가에 따른 누설 유동의 증가로 인하여 수력학적 성능이 감소한 것으로 볼 수 있다.

Fig. 6

Streamline and vector distribution on guide vanes and guide vane blade views with 1 mm clearance and without clearance

3.3 표면조도에 따른 성능 특성 비교

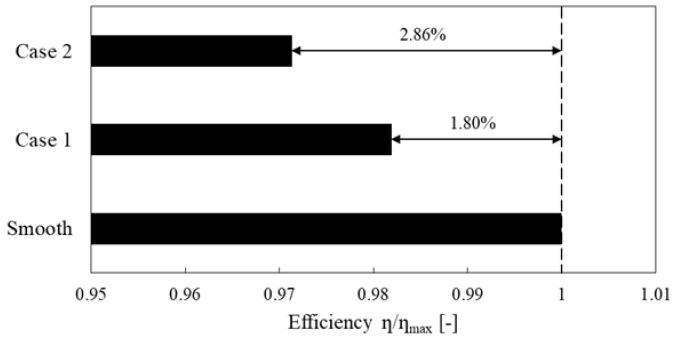
본 연구에서는 상사된 프란시스 수차 축소 모델 내 표면조도에 따른 성능 및 내부유동 특성을 분석하기 위해 정격 운전조건에서 정상상태의 삼차원 해석을 수행하였다. Fig. 7은 프란시스 수차 축소 모델의 앞서 언급한 표면조도에 따른 효율을 비교하고 있다. Fig. 7에서 볼 수 있는 바와 같이 수차모델에서 표면조도가 없는 부드러운 벽면과 비교하여 볼 때 IEC 규격에서 제시하는 표면조도인 Case 1과 제시된 표면조도의 2배 값인 Case 2에 나타난 효율은 프란시스 수차 축소모델의 표면 조도가 커짐에 따라 현저히 감소하는 경향을 보였고, 정량적으로 비교하여 볼 때 Case 1과 Case 2는 각각 1.80% 및 2.86% 정도의 효율 감소를 보였다.

Fig. 7

Efficiency comparison of Francis hydro turbine model with various surface roughness

Fig. 8은 표면 조도에 따른 프란시스 수차 모델 내 주요 구성요소의 손실 계산 결과를 보여주고 있다. 프란시스 수차 축소 모델의 손실계산은 러너를 제외한 스파이럴 케이싱, 스테이 베인, 가이드 베인 및 드래프트 튜브에 대해서는 식 (9)을 사용하였고, 러너에 대한 손실계산은 식 (10)을 사용하였다.⁽²⁾

Fig. 8

Loss distribution of each component with various surface roughness

여기서, H_loss는 손실을 낙차로 나타낸 값이고, Δp_total 은 각 구성요소의 전압력 차 및 ρ는 물의 밀도를 나타낸다. 더불어 H_{loss runner}의 T는 러너의 토크값 및 ω는 각속도를 나타낸다.

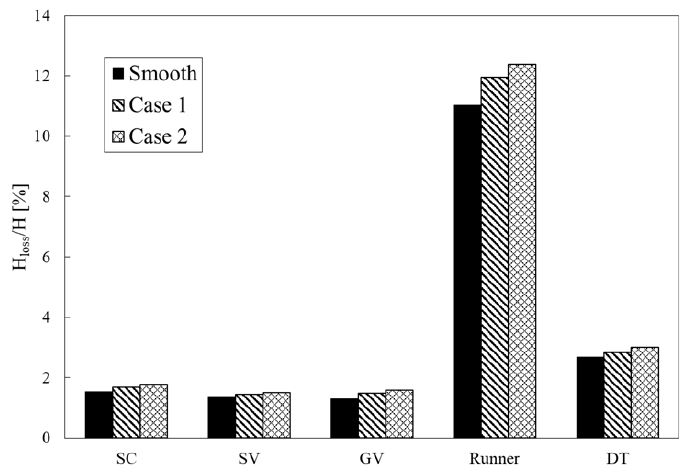
Fig. 8을 살펴보면 프란시스 수차 축소 모델의 표면 조도가 증가함에 따라 각 주요 구성요소에서 손실이 약간씩 증가하는 것을 볼 수 있으며, 러너의 경우에는 유속이 빠르기 때문에 다른 구성요소에 비해 손실 폭이 현저히 큰 것을 확인할 수 있다. 이와 같이 표면조도가 커질수록 프란시스 수차축소 모델의 각 구성요소에서의 손실이 증가하므로 전체적인 효율 저감이 나타난 것으로 볼 수 있다.

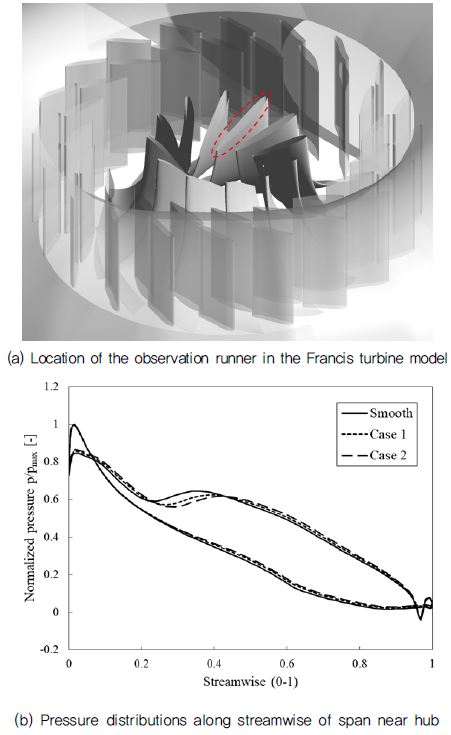
러너 블레이드에 대해 표면조도에 따른 압력 분포를 확인하기 위해 Fig. 9(a)와 같이 스파이럴 케이싱 설부(Tongue) 인근 위치의 러너 블레이드의 압력 분포를 확인하였다. Fig. 9(b)의 압력 분포는 러너 블레이드 허브 근처 스팬에서의 유동 방향에 따른 압력을 나타내며, 여기서 x 축의 0과 1은 각각 전연과 후연을 나타낸다. 압력값은 최대 압력값으로 나누어 무차원화 하였고, 압력 분포 그래프의 압력면과 부압면의 차이로 인해 형성된 면적은 성능을 나타낸다. 관찰된 러너위치의 영역은 유동교란이 심한 영역으로, 러너의 유동각이 맞지 않아 손실이 증가하여 전연의 압력면이 흡입면보다 낮은 압력특성을 보이고 있다. 한편 압력분포는 모두 유사한 경향을 보이지만, 표면조도가 증가함에 따라 특히 전연부 인근에서는 면적이 작아지는 것을 확인할 수 있다. 이와 같은 결과는 Fig. 8에서도 볼 수 있듯이 표면 조도 증가에 따른 러너의 손실로 인한 수력학적 성능 감소의 원인을 보여줌과 동시에 축소 모델 제작 시 반드시 고려해야할 중요한 형상 매개변수임을 잘 보여주고 있다.

Fig. 9

Pressure distributions along streamwise of runner

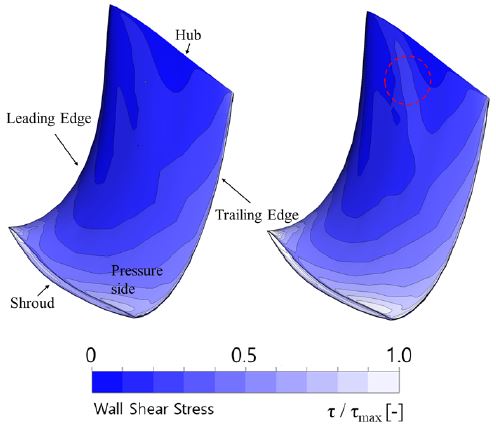
Fig. 10은 표면조도에 따른 벽 전단응력의 비교분석을 위해 Fig. 9(a)에 위치한 러너 블레이드에 대해 표면조도가 없는 부드러운 벽면과 표면조도 2배 값인 Case 2의 압력면을 나타내고 있다. 여기서 압력면의 벽 전단응력은 최대 응력값으로 나누어 무차원화하였다. 러너 벽면의 표면조도 증가에 따라 벽면 마찰이 증가하게 되고, 이에 따라 벽 전단응력도 증가하게 된다. 표면조도가 적용된 오른쪽 러너는 왼쪽의 부드러운 벽면을 가진 러너에 비해 상대적으로 높은 벽 전단응력을 확인할 수 있으며, 특히 표시된 부분의 영역은 허브 인근의 벽 전단응력의 차이를 뚜렷하게 확인할 수 있으며, 이는 Fig. 9(b)의 전연의 유동방향 0.3 부근의 압력면이 흡입면보다 낮은 압력특성에 대한 원인으로 볼 수 있다.

Fig. 10

Wall shear distributions on pressure side of runner with smooth surface (Left) and roughness surface (Right)

3.4 가이드 베인 간극 및 표면조도를 모두 고려한 성능 특성 비교

본 연구에서 고려된 형상 매개변수인 프란시스 수차 축소 모델의 가이드 베인 간극과 표면조도를 동시에 고려하여, 간극 및 표면조도 두개의 형상 매개변수에 따른 성능 특성 및 내부유동에 대한 영향을 정상상태의 삼차원 해석을 통해 비교 분석하였다.

프란시스 수차 축소 모델 가이드 베인 간극의 영향 분석을 위한 변수들에 표면 조도 Case 1을 적용하여 수치해석을 수행하였고, Fig. 11은 프란시스 수차 모델에 가이드 베인 간극과 표면 조도를 동시에 고려한 수치해석 결과로서, 두 형상 매개변수에 대하여 수차 효율에 미치는 영향을 비교하고 있다. Fig. 11에서 볼 수 있는 바와 같이 가이드 베인 간극 및 표면 조도가 동시에 작용하는 경우, 각각 형상 매개변수가 적용된 효율을 비교했을 때, 각 변수에 대한 효율 저하만큼의 감소한 효율을 보였다. 두 형상 매개변수를 동시에 고려했을 때 이들의 상호작용으로 인해 발생하는 뚜렷한 추가적인 손실은 수력학적 성능에는 나타나지 않았다. 이와 같은 결과로 비추어 볼 때, 프란시스 수차 축소 모델에 대해서는 가이드 베인 간극에 따른 영향보다는 표면 조도에 따른 영향이 프란시스 수차 축소 모델의 수력학적 성능에 더 많은 영향을 미치는 것을 확인 할 수 있다.

Fig. 11

Efficiency comparison of Francis hydro turbine model with various guide vane clearance and surface roughness