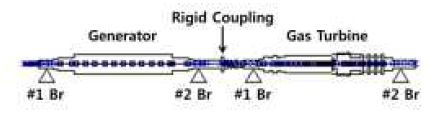
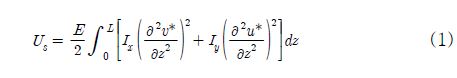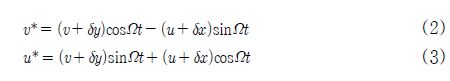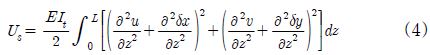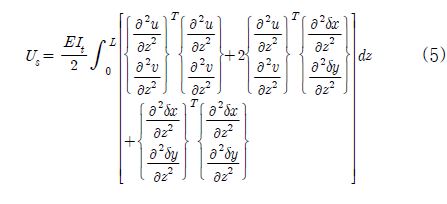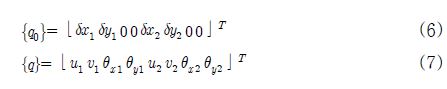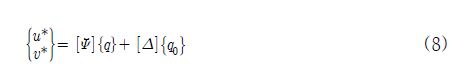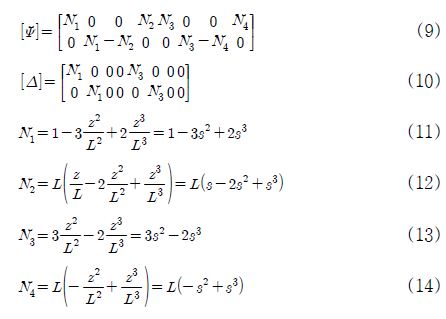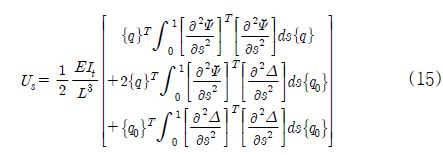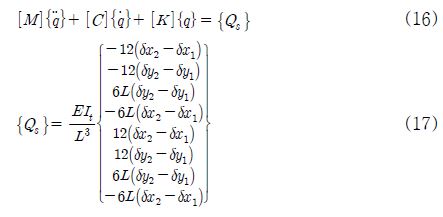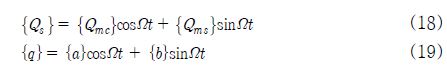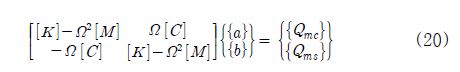Dynamic Response Analysis of a Heavy Duty Gas Turbine-Generator with Rigid Coupling Offset

1. 서 론

대형 발전용 가스터빈과 발전기는 고정 커플링(rigid coupling)으로 연결되며, 이들은 정격 운전속도 이내에서 1∼2개의 위험속도를 통과하는 유연한 로터 시스템이다. 이러한 로터 시스템의 경우는 불평형 질량 및 축 정렬, 축 초기변형 등의 요인에 의해 정격 운전속도이내의 위험속도에서 주로 가진되는 동적 응답 특성을 나타낸다.

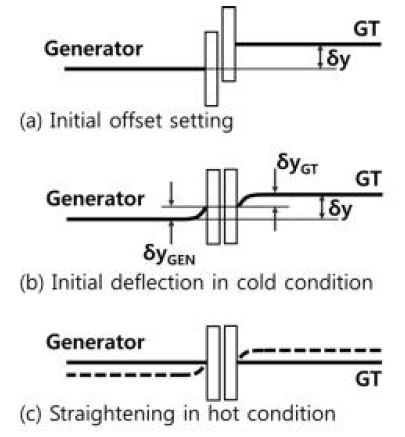
한편, 대형 발전용 가스터빈은 운전 중 cold 상태에서 hot 상태로 변화하면서 주로 터빈 지지부의 열팽창(thermal expansion) 및 발전기 전체 지지부의 열팽창이 나타남에 따라, 가스터빈 로터와 발전기 로터가 커플링부에서 각각 상하로 상대 이동이 발생하게 된다. 그리고, 가스터빈과 발전기가 고정 커플링으로 연결되는 경우에는 이러한 영향으로 인해 커플링부에서 굽힘 모멘트가 집중적으로 작용될 수 있다. 따라서, hot 상태에서의 커플링부에 작용될 수 있는 굽힘 모멘트를 최소화 하기위해, 먼저 가스터빈과 발전기를 고정 커플링으로 연결함에 있어서 열팽창에 의한 상대 이동량 만큼을 Fig. 1의 (a)와 같이 초기 오프셋으로 설정한다. 그리고, 각 로터의 고정 커플링을 조립함에 있어서 초기변위를 Fig. 1의 (b)와 같이 반영한다. 그러면, 가스터빈 운전 중 hot 상태에서는 열팽창에 의해 오프셋이 제거되어 Fig. 1의 (c)와 같이 나타날 것이다.

Fig. 1

Offset setting of rigid coupling and connection condition change by operation

Nicholas 외(12)는 축 초기변형(residual shaft bow)이 Jeffcott 로터 시스템의 불평형 응답에 미치는 영향과 밸런싱 방법을 제시하였으며, Kim 외(3)는 축 초기 변형을 갖는 Jeffcott 로터 시스템의 베어링 강성 변화에 대한 동특성 변화를 관찰하였다. 그리고, Nelson(4)은 축 초기변형을 갖는 단축 로터 시스템에 대해 유한 요소 모델링을 기초한 정상상태 동적 응답 해석 및 밸런싱 방법이 제시된 바 있다.

본 연구에서는 축 초기변위가 있음에 따라 로터-베어링 시스템의 정상상태 동적 응답을 구하는 일반화된 유한요소 모델이 제시된다. 그리고, 고정 커플링으로 연결된 대형 발전용 가스터빈과 발전기의 2축 로터 시스템에서 고정 커플링의 오프셋 조립을 축 초기변위로 반영하여, cold 상태 및 hot 상태에 대해 오프셋 변화에 따라 동적 응답 해석을 수행하고자 한다.

2. 초기변위가 있는 로터 시스템의 동적 응답

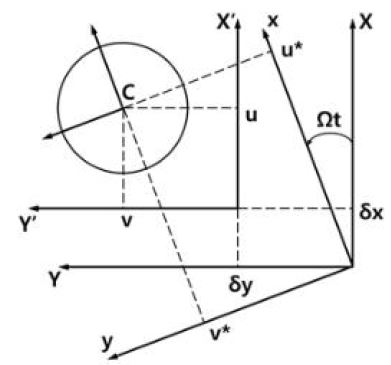
원형 단면을 갖는 축 요소의 일반 스트레인에너지는 축 중심 C의 x, y 좌표축에 대한 병진변위 u*와 v*으로 식 (1)과 같이 표현된다(5).

여기서, E는 탄성계수이고, I_x와 I_y는 횡 면적 관성모멘트, L은 축 요소의 길이이다. 그리고, Fig. 2와 같이 병진변위 u*와 v*는 초기 좌표계인 X, Y 좌표축에 대한 초기변위 δx, δy와 함께, 변위 u와 v로 다음과 같이 나타낼 수 있다.

따라서, 식 (2)와 (3)을 식 (1)에 대입하면, 초기변위를 갖는 원형 축 요소의 스트레인에너지에 대한 수식은 식 (4)와 같이 표현될 수 있으며, 이를 행렬로 표현하면 식 (5)와 같다.

Fig. 2

Coordinates of the geometric center C on the initial shaft deflection

Fig. 3

Shaft finite element and displacement vector with Initial deflection

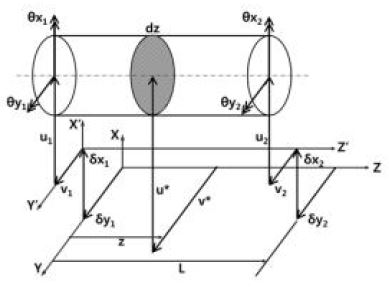
한편, Fig. 3은 축 요소의 양 끝단에서의 초기 변위벡터와 해당 변위벡터를 나타내고 있으며, 각각은 식 (6)과 (7)로 정의된다.

Fig. 4

FE model of gas turbine-generator rotor with rigid coupling

축 요소의 임의의 위치, z에 대한 병진변위 u*와 v*는 라그랑지 다항함수에 의해 축의 굽힘에 대한 근사적 보간을 통하여 식 (8)과 같이 병진변위 행렬로 나타낼 수 있으며, 이는 해당 변위벡터의 항과 초기 변위벡터의 항으로 표현된다.

여기서, 축 요소의 병진 거동에 대한 형상함수는 식(9)∼(14)로 정의되며, 계산의 편리성을 위해 z/L은 변수 s로 치환하였다.

식 (8)의 해당 변위벡터 행렬항과 초기 변위벡터 행렬항에 대해 변수 s에 대한 2차 편미분을 취하여 각각을 식(5)에 넣으면, 축 요소의 스트레인에너지는 식 (15)와 같이 정리된다.

그리고, 식 (15)에 라그랑지 방정식을 적용하면 축 요소의 운동방정식 중에서 강성 행렬항과 함께 외력 행렬항이 나타나고, 최종적으로 디스크 및 축, 베어링 요소로 구성된 전체 로터-베어링 시스템의 운동방정식은 초기변위에 의해 발생된 외력항과 함께 식 (16)과 (17)로 나타낼 수 있다.

초기변위에 의해 발생된 외력에 대한 동적 응답해석을 위해 일반화된 가진력과 가정된 해는 식 (18)과 (19)로 표현된다.

식 (18)과 (19)를 식 (16)에 대입하여 정리하면, 식 (20)과 같이 초기변위에 의해 발생된 외력에 대한 동적응답 방정식이 얻어지며, 이로부터 구하여진 동적응답 해의 계수를 통하여 축의 각 절점에서의 동적응답 궤적을 구할 수 있다.

3. 가스터빈-발전기의 해석 결과

Fig. 4는 대형 가스터빈-발전기의 로터-베어링 시스템 FE 모델이며, 고정 커플링으로 연결된 가스터빈과 발전기 축-요소, 각 지지 베어링-요소, 집중 질량-요소 등으로 구성되어 있다(6).

여기서, 고정 커플링의 오프셋 설정을 0.1mm, 0.2mm, 0.4mm, 0.6mm의 총 4가지 경우로 가정하여 가스터빈-발전기 로터 시스템의 커플링부 초기변위의 외력으로 반영하였으며, 발전기의 2개 베어링 위치와 가스터빈의 2개 베어링 위치에서의 동적 응답 해석을 수행하였다. 단, 불평형 질량은 반영하지 않았다.

3.1. 초기변위가 유지되는 경우(cold 상태만 고려)

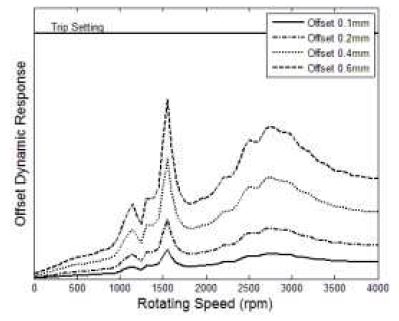
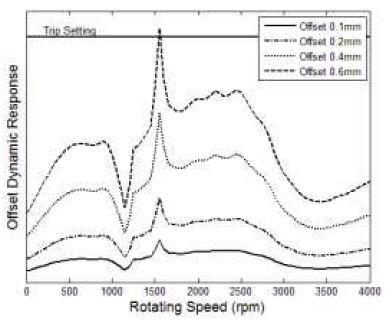
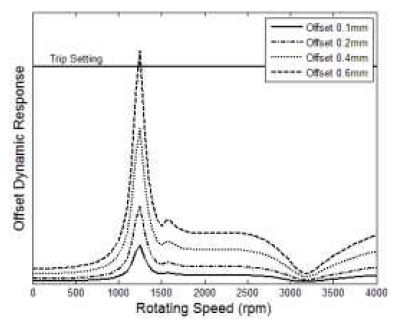
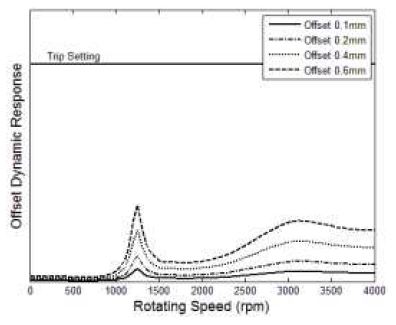
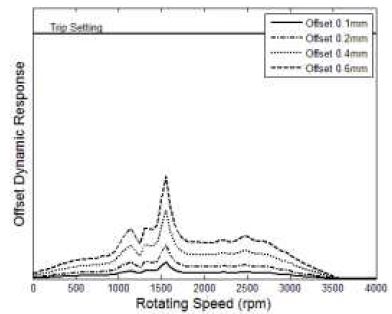
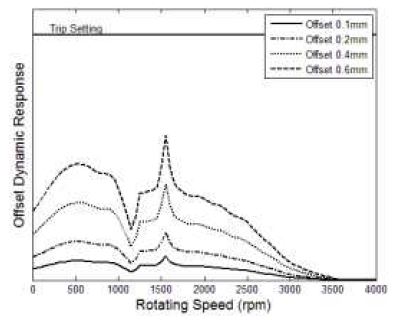
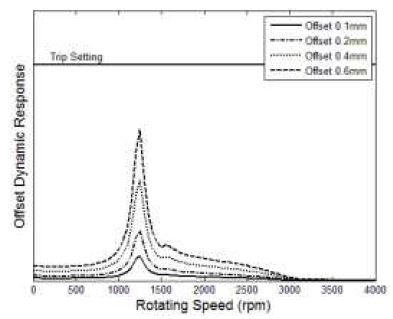
먼저, 고정 커플링에 반영된 초기변위가 회전속도의 증가에 따라 cold 상태의 오프셋 설정을 동일하게 유지함을 가정하였으며, 이 경우에 대한 발전기의 #1 베어링과 #2 베어링 위치에서의 동적 응답 결과를 Fig. 5와 6에 나타내었다. 기본적으로 초기변위 증가량만큼 동적 응답의 레벨 증가는 선형적으로 증가하는 것으로 보여졌다. 그리고, 응답 특성은 주로 위험속도 영역에서 가진되어 나타났으며, 초기변위가 증가할수록 각 위험속도에서의 응답 특성은 더 커지고 뚜렷하게 나타났다. 특히, 고정 커플링과 근접한 #2 베어링 위치에서의 동적 응답은 #1 베어링 위치에서보다 상대적으로 크게 영향 받는 것으로 확인되었으며, 0.6mm 오프셋의 경우에는 발전기 진동 trip 설정을 일부 넘어서는 것으로 예측되어졌다. 한편, 가스터빈의 #1 베어링과 #2 베어링 위치에서의 동적 응답 결과는 Fig. 7과 8에 나타내었다. 초기변위 가진에 대해 가스터빈의 동적 응답 특성은 발전기와 동일한 경향을 나타내고 있으며, 가스터빈은 고정 커플링과 근접한 #1 베어링 위치에서의 동적 응답이 #2 베어링 위치에서보다 상대적으로 크게 나타났다. 또한, #1 베어링 위치에서 0.6mm 오프셋의 경우에 가스터빈 진동 trip 설정을 일부 넘어서는 것도 확인되었다.

Fig. 5

Dynamic response at #1 bearing of the generator in case of retaining each offset

Fig. 6

Dynamic response at #2 bearing of the generator in case of retaining each offset

Fig. 7

Dynamic response at #1 bearing of the gas turbine in case of retaining each offset

Fig. 8

Dynamic response at #2 bearing of the gas turbine in case of retaining each offset

3.2. 초기변위가 줄어드는 경우(cold 상태에서 hot 상태로 변화 고려)

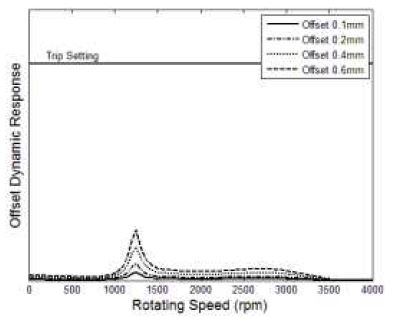
다음은, 고정 커플링에 반영된 초기변위가 회전속도가 증가함에 따라 cold 상태에서 hot 상태로 변화하면서, cold 상태의 오프셋 설정이 유지되지 못하고 선형적으로 감소하여 정격 운전속도에서는 제거되도록 가정하였다. 이 경우에 대한 발전기의 #1 베어링과 #2 베어링 위치에서의 동적 응답 결과를 Fig. 9와 10에 나타내었다. 본 오프셋의 변화에 대한 동적 응답 특성은 앞서 Fig. 5, 6과 동일한 경향을 나타내지만, 회전속도가 증가함에 따라 동적 응답 레벨은 앞선 결과 보다는 낮아졌으며 정격 운전속도에서는 동적 응답이 거의 나타나지 않는 것으로 확인되었다. 특히, 고정 커플링과 근접한 #2 베어링 위치의 동적 응답이 상대적으로 민감하게 영향을 받았으며, 0.6mm 오프셋의 경우에 대한 동적 응답은 앞선 결과보다 최대 40%이상 감소함에 따라 발전기 진동 trip 설정 아래에 있는 것으로 예측되었다. 한편, 가스터빈의 #1 베어링과 #2 베어링 위치에서의 동적 응답 결과는 Fig. 11과 12에 나타내었다. 본 경우의 초기변위 가진에 대해 가스터빈의 동적 응답 특성은 앞선 발전기와 동일한 경향을 나타내고 있다. 그리고, 가스터빈도 역시 고정 커플링과 근접한 #1 베어링 위치의 동적 응답이 상대적으로 민감하게 영향을 받았으며, 0.6mm 오프셋의 경우에 대한 동적 응답은 앞선 Fig. 7과 8의 결과보다 최대 35%이상 감소함에 따라 가스터빈 진동 trip 설정 아래에 있는 것으로 확인되었다.

Fig. 9

Dynamic response at #1 bearing of the generator in case of reducing each offset

Fig. 10

Dynamic response at #2 bearing of the generator in case of reducing each offset

Fig. 11

Dynamic response at #1 bearing of the gas turbine in case of reducing each offset

Fig. 12

Dynamic response at #2 bearing of the gas turbine in case of reducing each offset

4. 결 론

본 연구에서는 축 초기변위를 고려한 로터-베어링 시스템의 정상상태 동적 응답의 일반화된 유한요소 모델을 수립하고, 고정 커플링으로 연결된 대형 발전용 가스터빈과 발전기의 2축 로터 시스템에서 고정 커플링의 오프셋 변화에 따라 cold 상태 및 hot 상태에 대한 동적 응답 해석을 수행하였으며, 그 결과를 요약하면 다음과 같다.

1) 축 초기변위는 불평형 질량과 함께 외력항으로 로터 시스템에 작용하며, 초기변위만을 고려할 때 초기변위의 배수 증가에 따라 동적 응답도 거의 동일한 선형적 배수 증가의 특징이 있음이 확인되었다.

2) 본 가스터빈-발전기 로터는 고정 커플링으로 오프셋 정도에 따라 주로 정격 운전속도이내의 각 위험속도에서 동적 응답이 크게 나타날 수 있지만, cold 상태에서 hot 상태로 변화되면서 고정 커플링의 초기변위가 자동적으로 저감되고 동적 응답의 영향도도 현저히 감소됨에 따라, 정격 운전속도에서 지속적 운전시에는 커플링의 오프셋 영향은 거의 없을 것으로 판단된다.

Acknowledgments

본 연구는 2013년도 산업통상자원부의 제원으로 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구과제입니다. (No. 2013101010170A)

References

• Nicholas, J. C., Gunter, E. J., Allaire, P. E., “Effect of Residual Shaft Bow on Unbalance Response and Balancing of a Single Mass Flexible Rotor, Part 1: Unbalance Response”, Journal of Engineering for Power, Trans. ASME, (1976), 98(2), p171-181.
• Nicholas, J. C., Gunter, E. J., Allaire, P. E., “Effect of Residual Shaft Bow on Unbalance Response and Balancing of a Single Mass Flexible Rotor, Part 2: Balancing”, Journal of Engineering for Power, Trans. ASME, (1976), 98(2), p182-187.
• Kim, Y. C., Kim, B. K., Kim, B. O., “A Study on the Dynamic Characteristics of a Shaft with Initial Deflection”, Transactions of Korean Society of Automotive Engineers, (1998), 6(6), p80-87.
• Nelson, H. D., “Steady Synchronous Response and Balancing of Rotor Systems with Residual Shaft Bow”, International Journal of Rotating Machinery, (2002), 8(6), p431-438. [https://doi.org/10.1155/S1023621X02000416]
• Lalanne, M., Ferraris, G., Rotordynamics Prediction in Engineering, John Wiley, (1998).
• Ha, J. W., Lee, A. S., “Rotordynamic Design Sensitivity Analysis of a Heavy Duty Gas Turbine- Generator”, Proceedings of 2012 Annual Meeting of Korean Fluid Machinery Association, (2012), KFMA_2012_OP07074.