축류팬 임계속도 예측에 대한 연구

1. 서 론

축류팬(Axial Fan)은 대형 교통수단 및 산업용 환기시스템으로 사용되는 산업설비로서 다양한 도로와 광역철도, 지하철 등의 터널에 주로 사용하고 있다. 특히 폐쇄된 공간에서의 제연 및 배연은 인명보호차원에서 매우 중요하며 사고 발생시 이를 대비하기 위해 중요한 설비이다.

고효율의 축류팬 설계 및 기술개발은 축류팬의 작동유체를 주로 공기를 사용하는 이유로 공력학적 성능 및 효율 극대화를 위해 날개(Blade)의 개수 및 형상과 가이드 베인(Guide Vane)의 형상 설계 등에 대한 연구는 활발히 진행되어 왔다.^(1,2)

축류팬 형상에 대한 구조해석에 대한 연구는 유체-구조 연성해석 기법을 이용한 플라스틱 축류팬의 날개 진동특성 평가⁽³⁾와 소음특성⁽⁴⁾에 대한 내용이 주를 이루어 왔다.

대형 축류팬의 구조해석에 대한 연구는 기초적인 연구만 진행되어 임계속도와 관련된 연구는 미흡한 부분이 많았다. 또한 축류팬의 주요 구성요소인 임펠러(Impeller)를 구성하는 요소에 대해서는 구조적 강도에 대해서는 관심을 가지지 못하였다. 구조적 강도를 고려하기 위해서는 사용하는 재질에 대한 인장시험을 통해 여러 가지 물성치의 정보가 필요하고 이를 기초로 재질의 특성이 고려된 임펠러의 설계가 병행되어야 한다.

일반적으로 대형 축류팬의 임계속도를 측정하기 위해 회전체의 위험성을 고려하여 과속도 시험 장치를 개발하는데 시험 시 파손에 의한 인명 피해를 방지하기 위한 안전장치 및 이와 관련된 표준규격에 맞는 시험장치 제작하는 데에 많은 어려움이 있어 시뮬레이션을 통한 임계속도 예측에 대한 산업현장의 요구가 있었다.

본 연구는 과속도 시험장치를 이용한 예상 임계속도를 도출하기 위해 3차원 모델링을 활용하여 실제 송풍기의 임펠러 형상을 구현하고자 하였으며 날개와 허브(Hub)의 가공에서 차이를 보여 실제와 동일하다고 가정하고 해석 형상으로 사용하였다.

회전수에 따른 임계속도를 도출하기 위해 상용 유한요소 해석 프로그램(SolidWorks Simulation)으로 정적구조해석⁽⁵⁾을 수행하였다. 정적구조해석을 통해 운전속도별 최대응력을 도출하고 재료의 소성영역과 탄성영역을 구분하여 응력을 분류하였다.

재료의 특성인 연성과 취성에 대한 안전계수를 도출하여 유한요소해석적 임계속도를 도출하고자 하였다. 정적구조해석으로 도출된 임계속도에 대한 결과를 반영하여 과속도 시험장치의 설계 및 시험을 진행하여 임계속도를 파악하기 위한 연구를 진행하였다.

2. 이 론

2.2 일반적인 파괴이론

연성은 복합응력상태에서 응력들의 조합으로 나타나게 되는 폰-미세스 응력(Von-Mises Stress)과 재료의 항복응력에 접근하는 상태에 따라 소성변형을 판단하며 이후 변형정도에 따른 소성변형에서 파손에 대한 예측을 하게 된다. 등방성 재료의 파손조건은 수학적으로 식 (1)과 같이 나타낼 수 있다.

$\[ f\left({\sigma }_1,{\sigma }_2,{\sigma }_3\right)={\sigma }_c \]$

(1)

σ₁ , σ₂, σ₃: Principle Normal Stress, σ_c: Compress Stress

연성의 항복응력과 폰-미세스 응력으로 계산되는 안전계수(X₁)는 식 (2)와 같다.

$\[ X_1=\frac{{\sigma }_y}{{\sigma }_v} \]$

(2)

X₁: Safety Factor(FOS) of Ductility
σ_ν: Von-mises Stress, σ_y : Yield Stress

취성의 가장 간단한 형태의 파손이론은 최대 수직응력 파괴조건(Maximum Normal Stress Fracture Criterion)으로 주 수직응력이 인장 위주의 하중을 받는 취성의 파괴를 예측하는데 적합하다. 재료의 항복과 인장이 명확하게 구분되지 않고 최대강도에서 파손이 발생하게 된다. 따라서 취성은 파손 가능성에 대해 주응력(Principle Normal Stress)으로 판단하게 되며 이러한 재료에서 수직응력 파손 조건은 함수형태로 식 (3)과 같은 함수형태로 나타낼 수 있다.

$\[ {\sigma }_y=MAX\left(\left|{\sigma }_1\right|,\left|{\sigma }_2\right|,\left|{\sigma }_3\right|\right)\left(at fracture\right) \]$

(3)

(σ₁,σ₂,σ₃: Principle Normal Stress, σ_y: Yield Stress)

MAX는 각 주응력에 대한 최대값을 의미하고 인장과 압축응력을 표현하기 위해서는 (+)와 (-)를 사용하게 되는데 최대 주응력을 구현하기 위해 절대값을 사용하게 된다. 이는 압축성 주응력을 고려하기 위해 사용하는 것으로 가해준 최대 응력에 대한 특별한 조합을 유효응력으로 표기할 수 있고 식 (4)와 같다.

$\[ {\stackrel{-}{\sigma }}_N=MAX\left(\left|{\sigma }_1\right|,\left|{\sigma }_2\right|,\left|{\sigma }_3\right|\right) \]$

(4)

(σ_N : Maximum Normal Stress Condition)

최대수직응력조건과 재료에 주어진 항복응력과의 관계로서 파손여부를 예상할 수 있으며 이를 안전계수(X₂)라고 정의하고 관련 수식은 식 (5)와 같이 나타낼 수 있다.

$\[ X_2=\frac{{\sigma }_u}{{\stackrel{-}{\sigma }}_N} \]$

(5)

X₂: Safety Factor(FOS) of Brittleness
σ_y: Yield Stress, σ_N: Maximum Normal Stress Condition

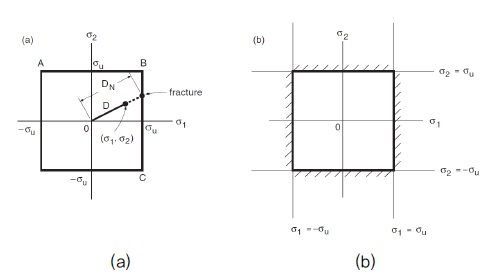
안전계수의 값이 1보다 작은 값을 가지게 되면 소형변형 및 파손이 일어날 가능성이 있으며, Fig. 1(a)에 나타낸 바와 같이 2차원 평면에서의 두 주응력 σ₁ 및 σ₂의 값이 파손 궤적 ABC를 벗어나게 되면 파손이 발생할 수 있다고 예상할 수 있다. Fig. 1(b)는 2차원 영역에서의 항복응력과 주응력의 교차되는 영역을 표시한 그림이다.^(6-8)

Fig. 1

Failure locus for the maximum normal stress fracture criterion for plane stress

2.3 원심력의 구조 이론

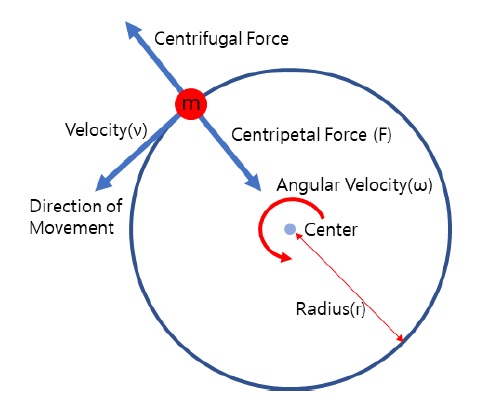
임펠러의 회전수에 따라 작용하는 힘을 산출하고자 할 때 원심력의 고려가 필요하다. 원심력은 이론적으로 식 (6)과 같이 나타낼 수 있으며, Fig. 2와 같이 도식화하여 설명할 수 있다.

Fig. 2

Centripetal force

임펠러의 날개와 허브로 구성된 회전체의 질량중심은 임펠러의 형상에 따라 위치가 바뀌게 되는 것을 고려하여야 한다.

$\[ F=ma=mr{\omega }^2=\frac{m{v}^2}{r} \]$

(6)

F : Centripetal Force (N)
m : Mass (kg)
a : Acceleration (m/s²)
r : Radius (m)
ω : Angular Velocity (m/s²)
v : Velocity (m/s)

3. 연구대상

3.1 축류팬 사양

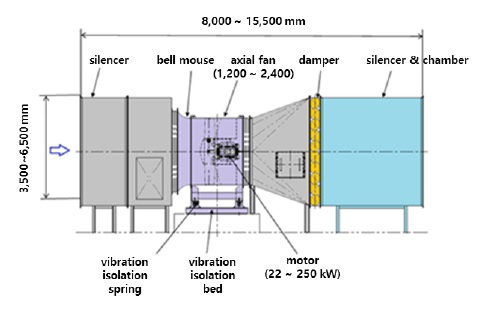
본 연구는 250마력급 축류팬 모델로 선정하였으며, 축류팬 시스템은 Fig. 3과 같이 소음기(Silencer), 벨 마우스(Bell Mouse), 댐퍼(Damper), 모터(Motor), 가이드 베인 및 임펠러 등으로 구성되어 있다. 연구대상에 대한 설계 사양은 Table 1과 같다.

Fig. 3

System of axial fan(9)

Table 1

Design specifications of axial fan

축류팬의 임계속도를 확인하기 위해 구성요소에서 회전체인 임펠러를 연구대상으로 설정하였으며, 임펠러는 날개와 허브로 구성되어 있다.

3.2 재료 물성치

임펠러의 구성요소인 날개와 허브는 알루미늄 합금 계열인 AC4C-T6 재료를 사용하며 재료 물성치는 Table 2와 같다.

Table 2

Materials of impeller sections(10)

4. 유한요소해석

4.1 해석모델

임계속도에 대한 해석을 수행하기 위한 해석모델은 Fig. 4와 같이 날개와 허브로 구성되어 있다.

Fig. 4

Components of impeller

4.2 경계조건 및 유한요소모델

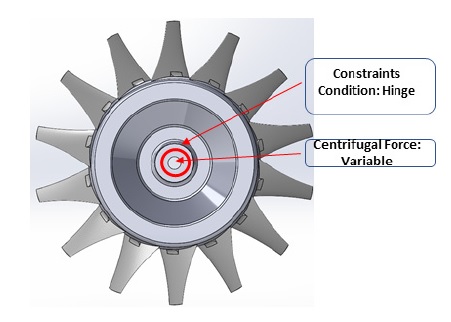
Fig. 5와 같이 구속조건에서 임펠러의 중심축을 기준으로 회전할 수 있는 조건을 부여하기 위해 힌지(Hinge)조건을 적용하였으며, 임계속도를 적용하기 위한 원심력 조건을 이용해 1200∼1700(r/min)까지 100(r/min)씩 증가시키며 해석을 진행하였다.

Fig. 5

Boundary condition

Fig. 6은 임계속도에 대한 해석을 진행하기 위해 생성된 유한요소모델로서 사면체 요소를 사용하였고 날개 및 허브의 곡면 형상을 최대한 구현하기 위해 요소의 크기를 날개는 4 mm, 허브는 10 mm로 설정하여 절점(Nodes)은 약 363만개, 요소(Elements)는 244만개로 구성하였다.⁽¹¹⁾

Fig. 6

Finite element shape of operating speed

4.3 해석결과

4.3.1 최대응력과 최대수직응력

Fig. 7은 운전속도의 변화에 따른 최대응력의 발생 위치를 대해 도시한 결과이다. 최대응력이 발생하는 부분은 날개와 허브를 조립하기 위해 설계된 허브 뭉치의 노치부에서 주로 발생하며 형상의 급격한 변화로 인해 발생하는 것으로 이는 재료 강도학적 이론⁽⁶⁾에서 제시되어 있는 내용과 일치한다.

Figs. 8 및 9는 식 (1)∼(5)에서 언급한 재료의 탄성영역 및 소성영역의 성질에 따른 파손 가능성에 대한 이론과 재료의 특성에 따라 분류하는 응력 이론의 적용 가능성을 확인한 결과이다. Fig. 8은 재료의 특성이 연성일 경우 탄성변형 및 소성변형에 대해 예측할 수 있는 폰-미세스 응력이며 Fig. 9는 취성일 경우 탄성변형과 소성변형을 비교하기 위해 최대수직응력(Max. Normal Stress : MPa)이며 각각 최소 운전속도인 1200(r/min)과 최대 운전속도인 1700(r/min)에 대한 것이다. 최대응력이 발생하는 지점은 동일하며 회전속도 및 분석하는 응력의 특성에 따라 최대응력 값의 차이를 확인할 수 있다.

Fig. 8

Maximum von-mises stress of impeller (MPa)

Fig. 9

Maximum normal stress of impeller (MPa)

4.3.3 재료 특성별 안전계수(Factor of Safety) 비교

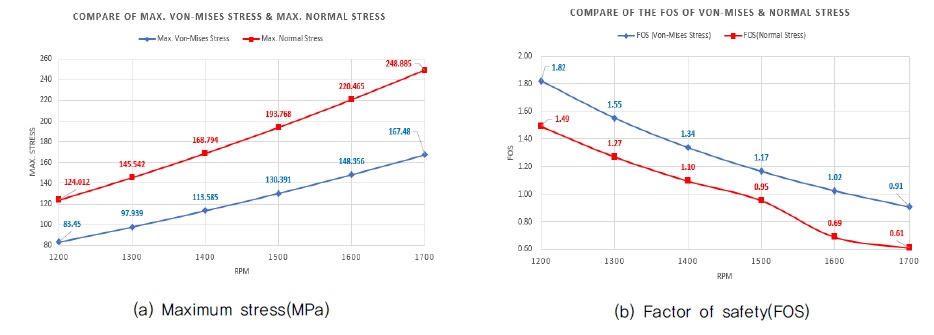
Fig. 10(a)는 최대 폰-미세스 응력과 최대 수직응력을 비교한 그래프이다. 운전속도가 증가할수록 최대응력은 공통적으로 증가하는 것을 확인할 수 있는데, 운전속도가 증가함에 따라 두 응력의 차이가 다소 커지는 것을 볼 수 있다. 이것은 폰-미세스 응력은 3차원 응력상태에서의 응력의 합산으로 이루어지고 인장하중과 압축하중을 모두 반영하기 때문에 운전속도에 따라 최대응력에 비해 상대적으로 작은 증가를 보이며, 최대 수직응력은 인장방향의 응력만을 주로 고려하기 때문에 증가폭이 폰-미세스 응력에 비해 증가폭이 큰 것으로 판단할 수 있다.

Fig. 10

Compare of maximum stress & factor of safety(FOS)

Fig. 10(b)는 유한요소해석을 통해 도출된 임펠러의 최대응력을 재료의 특성인 항복응력을 기준으로 운전속도별로 안전계수를 나타내었다.

연성인 경우 폰-미세스 응력을 기준으로 1,600∼1,700(r/min)에서 파손이 발생할 수 있으며, 취성인 경우 수직응력을 기준으로 임계속도는 1500(r/min)에 근접한 운전속도에서 파손이 일어날 것으로 예상되었다.

Table 3은 연성으로 가정하여 최대 폰-미세스 응력과 항복응력을 반영한 안전계수를 운전속도별로 나타낸 것이며, Table 4는 취성을 가정하여 최대 수직응력과 항복응력을 반영한 안전계수를 나타내었다.

Table 3

Maximum von-mises stress of impeller

Table 4

Maximum normal stress of impeller

5. 과속도 시험

5.1 시험 장치

과속도 시험은 ㈜삼원이앤비에서 실시하였으며, 최대 회전수는 1,700(r/min)까지 설정하여 시험을 진행하였다.

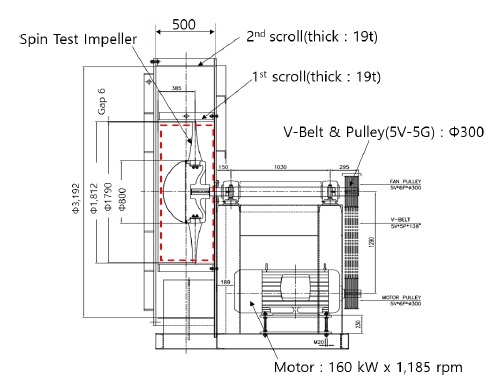
Fig. 11은 과속도 시험장치⁽¹²⁾의 구성도이며 Fig. 12는 과속도 시험장치를 제작한 그림이다. 실험장치의 구성요소는 시료인 송풍기를 회전시키기 위한 모터, 벨트 풀리(Belt pulley) 및 임펠러의 파손 시에 안전성을 최대한 고려한 2중의 보호철판(19 t)으로 되어 있으며 안전공간을 확보하도록 제작하였다.

Fig. 11

Configuration of overspeed test device

Fig. 12

Overspeed test device

5.2 시험 방법

Table 5는 과속도 시험을 하기 위한 모터의 주파수 증가에 따른 환산 회전수 및 임펠러 팁의 속도인 선속도에 대한 표로 나타내었다. 화재시 제연 기능을 수행하기 위해 60 Hz 이상으로 기동하여 제연기능을 수행하여야 하므로 60 Hz 이상의 작동조건에서 실제 시험을 통해 파손여부를 확인하여 안전성을 확보하고자 하였다.

Table 5

Converted rotational speed and circumferential speed according to frequency increase

주파수를 45 Hz에서 5 Hz씩 점진적으로 증가시켜 파손이 일어나는 주파수를 측정하고 이를 환산하여 임펠러의 임계회전수를 산출하는 방법을 사용하였다.

5.3 시험 결과

Fig. 13은 과속도 시험과정에서 임펠러가 파손된 결과를 나타낸 그림이다. 실험 임펠러는 파손된 주파수는 약 57 Hz의 작동조건에서 파손이 발생하였으며, 55∼60 Hz로 운전속도를 증가시키는 과정에서 급격한 회전수 증가로 인해 상온상태에서의 취성이 특성이 지배적인 약 1,500(r/min) 조건에서 파손되었다. 1,500(r/min)에서 파손되기 전에 진동과 소음이 발생하였으며, 그 이후에 파손이 발생하였다. 파손이 발생할 때의 운전속도를 감안하면 임펠러의 선속도는 140 m/s로 예상할 수 있다.

Fig. 13

Impeller breakage

6. 결 론

본 연구는 축류팬의 임계속도에 대해 유한요소해석을 통해 운전속도를 1,200(r/min)에서 1700(r/min)까지 100(r/min)씩 증가시키며 최대응력을 도출하였다.

재료강도학적으로 탄성영역과 소성영역의 이론을 적용하여 안전계수를 도출하기 위한 해석과 안전계수를 판단하기 위해 재료의 항복응력을 기준으로 정하였다.

재료 특성인 연성과 취성의 재질을 고려한 폰-미세스 응력과 최대수직응력을 통해 각각 안전계수를 산출과 재료 특성을 파악을 위해 과속도 시험을 실시하였고 파손이 발생하는 운전속도와 유한요소해석의 결과를 비교함으로써 임펠러를 구성하는 날개와 허브의 재질(AC4C-T6) 특성을 도출하였다.

과속도 시험장치의 설계 및 시험을 통해 임계속도를 파악하고 정적구조해석으로 도출된 결과를 비교하여 아래와 같은 결론을 얻었다.

• 1) 임펠러의 구성요소인 날개와 허브의 재료 특성을 고려할 때 연성일 경우 최대응력은 약 33% 작은 값을 보이고 취성을 경우에는 인장방향의 하중만 고려하고 취성의 특성상 소성변형 구간이 짧아지는 것을 확인하였다.
• 2) 유한요소해석으로 산출된 최대 폰-미세스 응력과 최대 수직응력을 항복응력을 기준으로 각각의 안전계수를 계산하고 연성의 경우 1,600∼1,700(r/min)에서 취성의 경우 1,500(r/min)에서 파손이 발생할 수 있다는 결과를 도출하였다.
• 3) 과속도 시험에서 회전수 1,500(r/min)에서 파손이 발생하였고 유한요소해석 결과와 일치하여 취성에 가까운 성질을 가지고 있으며 추후 AC4C-T6 재질을 이용해 다른 임펠러를 설계하는 경우에 취성의 특성을 반영한 설계가 필요하다.

Acknowledgments

본 연구는 한국생산기술연구원의 가역형 축류팬의 동적 구조해석에 대한 연구 용역 지원을 받아 수행하였으며, 이에 감사드립니다.

References

• Yang, S.H, Kim, K. Y., Hoe, M. W., 2018, “Effects of Geometric Parameters on Aerodynamic Performance of a High Pressure Axial Flow Fan,” The KSFM Journal of Fluid Machinery, Vol. 21, No. 6, pp. 32∼38. [https://doi.org/10.5293/kfma.2018.21.6.032]
• Lee, S.G, Lee, K. Y., Yang, S. H., Choi, Y. S., 2019, “A Study on Performance Characteristics of an Axial Fan”
• Chan Lee, Hyo Sang Kim, Hyun Gwon Kil, 2019, “Evaluation on the Blade Vibration Characteristics of a Plastic Axial Flow Fan Using Flow-Structure Coupled Analysis Technique,” The KSFM Journal of Fluid Machinery, Vol. 22, No. 5, pp. 21∼27. [https://doi.org/10.5293/kfma.2019.22.5.021]
• Dong-Hyun Kim, Yi-Jun Park, Hyun-Gwon Kil, Chan Lee., 2019, “A Study on the Design of Pod Type Circular Silencer with Two Air Layers for High Pressure Axial Fan”, Proceedings of the KFMA Annual Meeting, 2019.7, 212-213
• Kurowski and Paul, 2018, Sdc Pubns, “Engineering Analysis With Solid Works Simulation 2018” .
• Timoshenko, 1970, McGraw-Hill, “Theory of Elasticity”
• Norman E. Dowling, 2015, “Mechanical Behavior of Materials (Engineering Method for Deformation, Fracture, and Fatigue)”
• James M. Grere, Barry J. Goodno, 2014, “Mechanics of Material – SI Edition”
• Jeong Kuen Kook, Byung Kwan Cho, Sang Ho Yang, 2021, “A Study on Structural Characteristics of Axial Fans Operating Speed Using Finite Element Analysis,” Korea Academia-Industrial cooperation Society, Vol. 22, No. 2, pp. 593∼601.
• http://www.matweb.com
• David V. Hutton, 2006, “Fundamentals of Finite Element Analysis”
• JIMS C-2002, 1975, “Safety Design and Inspection Codes for Tests of High Speed Rotors”, The Japan Society of Industrial Machinery Manufactures