열-음향 상호작용을 고려한 라디에이터 홴 덕트 최적화 연구
Abstract
Although radiators have been actively used to manage the high thermal energy of internal combustion engines, the market size is increasing despite the recent rapid growth of electric vehicles. Radiators for vehicles were usually used with fans for effective thermal management. Radiators and fans improved heat dissipation performance in various ways. However, the noise covered in the internal combustion engine is emerging as a new problem in electric vehicles. Accordingly, it is required to develop the radiator fan considering the aeroacoustic characteristics. Ducts that may affect heat dissipation performance are generally used for the noise reduction of the fans. Therefore, heat dissipation performance and aeroacoustic characteristics for three design variables determining the aspect ratio of the ducted radiator fan were analyzed in this study. The results calculated numerically were used for optimization after analysis using the response surface methodology. A clear difference in noise characteristics was found according to the receivers. The heat dissipation performance was more influenced by the duct than the noise, and the Nusselt number was improved by 2.54% through optimization. Appropriate duct optimization considering both heat dissipation performance and noise reduction is important to design the radiator fan.
Keywords:
Radiator fan, Duct design, Aeroacoustics, Noise reduction, Heat dissipation performance, Response surface methodology, Optimal design키워드:
라디에이터 홴, 덕트설계, 공력음향, 소음저감, 방열성능, 반응표면법, 최적설계1. 서 론
라디에이터는 방열 등을 목적으로 열에너지를 전달하는 열교환기이다. 내연기관 엔진이 갖는 높은 열에너지 관리를 위해 활발히 사용되었던 라디에이터는 최근 전기자동차 시장의 도래에도 시장 규모가 성장하고 있다.(1) 최근 개발되는 전기자동차는 주행거리와 성능확보를 위해 높은 에너지 밀도를 가진 배터리가 사용되는데, 이때 발생되는 높은 열에너지를 적절히 제어하기 위해서는 열관리 기술이 필수적이다. 따라서, 최근 개발되는 전기자동차의 배터리 관리 시스템에서는 효과적인 배터리의 열관리를 위해 냉각수를 활용한 강제순환 방식으로 열을 흡수하고, 라디에이터를 통해 방출하는 방식이 선택되고 있다.(2)
개선된 성능을 요구하는 새로운 라디에이터 개발을 위해 순수한 물, 산화 그래핀(graphene oxide), 그래핀 나노 리본(graphene nano ribon) 등의 나노유체를 사용하여 실험적으로 성능을 비교한 연구가 보고된 바 있다.(3) 새로운 형태의 라디에이터를 제작하기 위해 기존과 다른 비금속형 열교환기를 제시하는 등 다양한 측면에서 라디에이터 성능 향상을 위한 노력이 이루어졌다.(4) 하지만, 라디에이터의 단독적인 사용은 방열성능이 제한적이며, 고온의 냉각수가 신속하게 열을 방출하는데 어려움이 있다. 따라서, 높은 방열성능이 요구되는 최근 라디에이터는 홴을 병행하여 사용한다.
라디에이터 홴 연구는 실험과 해석적 방법에 기반하여 다양하게 수행되었다. 계산자원과 방법론의 발전으로 실험으로 관찰되기 어려운 국소 위치에 대한 유체 흐름 분포를 이해하고, 기하학적 분석이 용이한 수치해석에 기반한 라디에이터 홴 연구는 최근 활발히 수행되고 있다.(5,6) 이러한 연구들은 전산유체역학에 기반하여 홴의 성능을 향상시킴으로 라디에이터의 대류 열전달 성능을 높이는 것을 목표로 수행되었다.
최근 급격한 전기자동차 시장의 도래와 더불어 기존 내연기관에서 사용되었던 라디에이터 홴과는 다른 새로운 성능이 강조되고 있다. 라디에이터 홴은 그동안 방열성능 향상을 위해 다양한 측면에서 연구되었지만, 기존 내연기관의 엔진음에 묻혀있던 부품들의 소음이 최근 전기자동차에서는 새로운 문제로 드러나고 있다. 따라서, 라디에이터 홴 소음을 저감하기 위한 다양한 연구들이 이루어지고 있다. 라디에이터 홴에서 발생하는 유동소음의 근원을 찾기 위해 소음원 탐지, 유동 가시화, 날개 인근 유동장 측정 방법 등을 통해 유동소음 메커니즘을 규명하고자 하였다.(7) 특정 주파수 및 영역의 소음을 제거하기 위해서 블레이드 통과 주파수(blade passing frequency; BPF) 소음의 예측기법이 개발되었고(8), eccentric shroud를 적용하여 해당 BPF 소음을 저감하고자 하였다.(9) 댐핑의 폭, 각도 등을 설계변수로 라디에이터에 대한 공간 변형을 통한 소음 감소 연구도 수행되었다.(10) 또한, 마이크로폰을 활용하여 톤 소음을 측정 후 분석하여 상쇄시키는 능동형 소음저감 기술도 최근 활발히 연구되고 있다.(11)
라디에이터의 공간 변형 및 능동적 소음저감 기술은 제한된 공간의 실제 차량에 장착되기 어렵고, 비용으로 인해 실제로 적용되기 어려운 단점이 있다. 그렇기 때문에 여전히 대부분의 라디에이터 홴은 덕트를 활용한 소음저감 기술이 채택되며, 덕트 최적화를 위한 연구가 활발히 수행되고 있다.(12) 하지만, 소음저감을 위한 덕트 형상은 오히려 공기역학적 성능이 저하될 우려가 있다. 따라서, 본 연구에서는 라디에이터 방열성능과 소음을 동시에 고려한 덕트 형상을 반응표면을 통해 분석 후 최적화하였다.
2. 수치해석
2.1 해석모델
고속으로 운전되는 압축기 등과 다르게 저속으로 작동되는 홴 등의 회전기계는 유동에 미치는 영향이 미미한 비교적 작은 크기의 덕트가 사용된다. 따라서, 설계변경에 따른 방열성능 및 소음의 변화를 명확히 비교하기 위해 본 연구에서는 T 사(13)의 8.9 리터급 대형 디젤 엔진의 냉각에 사용되는 덕트형 라디에이터 홴을 사용하였다. 라디에이터 홴은 상용 CAD 프로그램 ANSYS Design Modeler와 CATIA를 사용하여 유동해석에 적절한 형상으로 수정하였다.
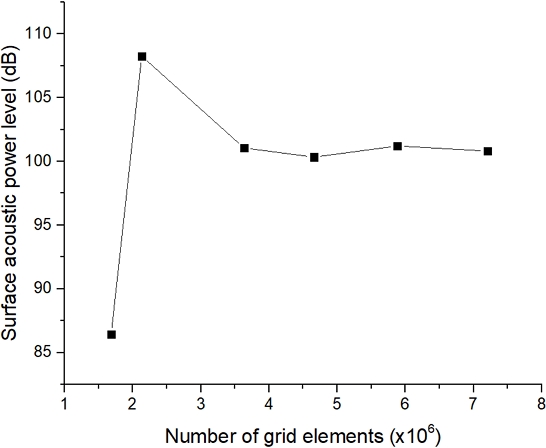
덕트를 포함한 복잡한 홴 형상의 원활한 격자 생성을 위해 사면체와 육면체 격자를 혼합하였으며, 벽면에 6개 이상의 계산 중첩층을 생성하였다. Fig. 1에 도시한 것처럼 약 168만 개에서 720만 개의 격자에 대해 홴 표면의 음향 출력 레벨을 비교하여 격자 의존도 검사를 수행하였으며, 약 363만 개 이상의 격자에서 의존성이 낮다고 판단 후 사용하였다.
2.2 지배방정식
생성된 유동장에 유한체적법 기반의 상용 CFD 코드인 ANSYS FLUENT를 사용하여 수치해석을 수행하였다. 질량보존을 만족시키기 위해서 식(1)의 시간변화를 고려한 연속방정식을 계산하였다.
| (1) |
여기서, ρ와 vi는 유체의 밀도와 속도를 의미한다. 밀도는 유체의 속도를 고려하여, 1.225 kg/m3의 상수로 계산하였다.
유동장을 비회전 영역과 회전 영역으로 나누어 운동량방정식을 계산하였다. 비회전 유동장에서는 직교좌표를 기준으로 식(2)의 운동량방정식을 계산하였다. 초기값 계산을 위해 좌측 첫 번째 항이 생략된 정상상태 운동량방정식을 계산하였다. 계산된 초기값을 바탕으로 식(2)의 모든항을 포함한 운동량방정식을 활용하여 비회전 영역에 대한 수치해석을 수행하였다.
| (2) |
여기서, p는 유체요소에 작용하는 압력이며, τij는 응력텐서를 의미한다.
라디에이터 홴 인근 유동장의 회전운동을 고려하기 위해 식(2)에 4개의 가속도항이 추가된 moving reference frame(MRF) 운동량방정식을 계산하였다. MRF 항을 포함한 운동량방정식은 아래 식(3)과 같다.
| (3) |
여기서, 2ω×vr은 Coriolis 가속도 항, ω×ω×r은 구심가속도 항을 의미한다. α×r와 a는 모두 선형가속도 항이며, a는 dvt/dt로 계산될 수 있다.
MRF 항이 포함된 운동량방정식에서도 좌측 첫 번째 항을 제외한 정상상태 방정식을 기반으로 초기값을 선정하였고, 식(3)의 모든 항을 포함한 방정식을 사용하여 시간분할을 고려한 최종 운동량을 계산하였다. 차량용 라디에이터 홴은 특성상 라디에이터의 상부에 위치한다. 따라서, 상하 비대칭 구조이기 때문에 격자를 직접 회전하여 계산을 수행하였다.
2.3 공력음향
수치 해석적으로 라디에이터 홴의 유동소음을 예측하기 위해 Lighthill(14)의 음향상사법(aeroacoustic analogy)에 기반하여 발전된 Ffowcs Williams-Hawkings(이하 FW-H)의 방정식(15)을 계산하였다. FW-H 방정식은 소음원과 청취자의 움직임도 고려할 수 있도록 발전되어 도플러 효과를 고려할 수 있다. 기존 덕트와 최적 설계된 덕트의 유동소음 비교를 위해 사용된 FW-H 방정식은 다음과 같다.
| (4) |
여기서, a0와 p′는 각각 원거리 장의 음속과 음압이다. 원거리 장의 음속은 일반적인 라디에이터 홴의 작동환경을 고려하여, 340 m/s의 상수로 설정하였다. 원거리 장의 음압은 p-p0로 계산된다. 음장의 기준 음압은 20 μPa을 사용하였다. δ(f)는 Dirac delta 함수, H(f)는 단위 계단(Heaviside) 함수, f는 경계 함수이다. 식(4)의 우측 첫 번째 항은 사중극자(quadrupole) 소음원에 기인한 난류 소음으로, 홴 후연(trailing edge)의 와류에 의한 소음 등을 의미한다. 두 번째 항은 쌍극자(dipole) 소음원에 기인한 하중 소음이다. 마지막 항은 홀극자(monopole) 소음원이며, 날개 표면에 의해 공기가 반복적으로 회전하며 발생하는 음파 펄스 등의 두께 소음이다. 적분 형태의 홀극자 소음원을 차원 분석하여, 아음속에서는 두께 소음이 지배적인 것을 알 수 있다.
2.4 경계조건
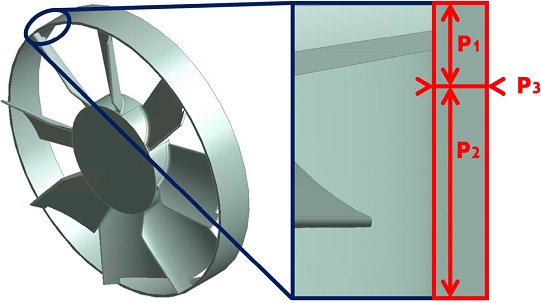
범용 라디에이터 홴의 성능분석을 위해 상온 및 대기압을 가정하여 수치해석을 수행하였다. 입출구 길이는 해석의 수렴성 및 완전 발달 유동을 고려하여 Fig. 2와 같이 수정하였다. 덕트에 의한 라디에이터의 방열성능을 비교하기 위해 열원(heat source)으로 도시된 라디에이터 표면에 일정 온도를 부여하였다. 열원은 배터리 냉각용 라디에이터의 온도를 고려하여, 333.15 K으로 설정하였다. 라디에이터 홴을 포함한 유체의 회전 영역(Fig. 2의 녹색)은 해당 온도에서 작동되는 홴의 최대 회전속도인 5,000 RPM으로 설정하였다. 수치해석에 사용된 입출구 및 열원의 경계조건은 Table 1로 정리하였다.
압력과 속도는 연립하여 계산하였고, 2차 차분화 기법을 기본으로 계산하였다. Shear stress transport(SST) k-ω 모델에 기반하여 초기값을 선정하였고, 계산된 초기값을 활용하여 large eddy simulation(LES) 모델을 통해 격자 크기에 따른 와류를 직접 계산하였다. 모델의 특성상 대부분의 에너지를 소산하는 아격자에 대한 별도의 모델링이 요구된다. 복잡한 대류에 의한 방열을 적절히 모사하기 위해 변형률과 회전률을 함께 고려하는 wall-adapting local eddy viscosity(WALE) 모델(16)을 사용하였다. 시간분할을 고려한 비정상 해석은 홴이 1° 회전하는 시간인 3.33×10-5을 기준으로 계산하였다.
유동해석 결과를 바탕으로 식(4)의 공력음향을 계산하였다. 소음 연구에서는 소음원과 더불어 청취자까지의 매질에 대한 물성치도 중요하게 고려해야 한다. 본 연구에서는 대기압의 공기(밀도 1.225 kg/m3)를 매질로 사용하였다. 기준 음압은 공기 중에서 최소 가청치를 기준으로 계산하였다. 수치해석 기법으로 예측된 공력음향은 Table 2의 12가지 청취자 위치에서 예측하였다. 최적화 모델과 기존 모델의 결과는 방열성능과 함께 비교하였다.
3. 최적설계
3.1 설계변수
본 연구에서는 Fig. 3에 도시한 덕트형 라디에이터 홴을 사용하였다. 저속 회전기계는 일반적으로 소음저감을 위해 덕트 형상을 추가한다. 하지만, 잘못된 덕트 설계는 홴의 공기역학적 성능을 저하시켜, 라디에이터의 본 목적인 방열성능에 악영향을 미칠 수 있다. 따라서, 본 연구에서는 라디에이터 홴 덕트의 형상을 결정하는 3가지 길이를 설계변수로 설정하여 최적설계를 수행하였다. 민감도 분석을 위해 설정된 설계변수는 라디에이터 홴 허브의 중심을 기준으로 덕트의 전단부를 P1, 후단부를 P2, 그리고 폭을 P3로 설정하였다. 라디에이터 홴 덕트 설계에 사용된 설계변수를 Fig. 3에 도시하였다. 각 설계변수의 범위는 기존 덕트의 크기를 포함하는 선에서 다른 부품과의 간섭이 생기지 않는 범위로 지정하였다. 따라서, P1은 3∼30 mm, P2는 8∼80 mm, P3는 6.5∼19.5 mm의 범위로 설계변수를 설정하였다.
3.2 목적함수
방열성능과 공력음향을 동시에 고려하기 위해 본 연구에서는 아래 두 가지 종속변수를 목적함수로 설정 후 다목적 최적화를 수행하였다. 라디에이터의 본 목적인 방열성능 확보를 위해 대류에 의한 효과를 최대화하며, 음압 변동의 최소화를 목적으로 최적화하였다.
덕트 형상에 따른 라디에이터의 방열성능을 비교하기 위해 Nusselt(Nu) 수를 계산하였다. 경계조건과 덕트를 제외한 형상은 고정된 값을 사용하였으며, 덕트의 형상만을 설계변수로 지정하였다. 목적함수로 사용된 Nu 수는 전도에 의한 열전달 대비 대류에 의한 열전달을 나타낸다.
| (5) |
여기서, h는 대류 열전달 계수, k는 열전도 계수를 의미한다. L은 라디에이터 표면의 Nu 수를 구하기 위해 설정한 특성 길이로, 1 m로 정하여 상대적 비율에 대해 고찰하였다.
수치 해석적으로 공력음향을 계산하기 위해서는 일반화된 방정식인 식(4)의 FW-H 방정식이 주로 사용된다. 하지만, FW-H 방정식은 과도해석을 기반으로 계산되기 때문에 많은 계산 비용과 시간이 소요된다. 이는 신속한 결과가 요구되는 산업현장 및 사전설계 단계에 적용하기 어려움이 있다.
저속 회전기계에서는 일반적으로 식(4)의 최우측 항인 홀극자 소음원이 지배적이다. 이는 날개로 인한 음파 펄스 등으로 대표할 수 있는 소음이며, 덕트 형상의 추가만으로도 간단하게 감소시킬 수 있다. 따라서, 덕트가 포함된 홴인 Fig. 3의 모델에서는 홀극자 소음원에 의한 소음이 지배적이지 않기 때문에 난류 소음인 사중극자 소음원과 하중 소음인 쌍극자 소음의 저감이 요구된다. 본 연구에서는 식(6)을 활용하여 음파의 매질 속 압력변동을 계산하는 광대역 소음원 모델을 활용하여 최적설계를 위한 목적함수로 사용하였다.
| (6) |
여기서, pref는 기준 음압이며, 1 kHz에서의 최소 가청치를 기준으로 한 20 μPa으로 계산하였다.
정상상태 기반으로 계산된 결과를 바탕으로 최적 모델을 예측하였고, 기존 모델과 최적화된 모델에 대해 과도해석을 통한 유동소음을 직접 계산하였다.
3.3 민감도 분석
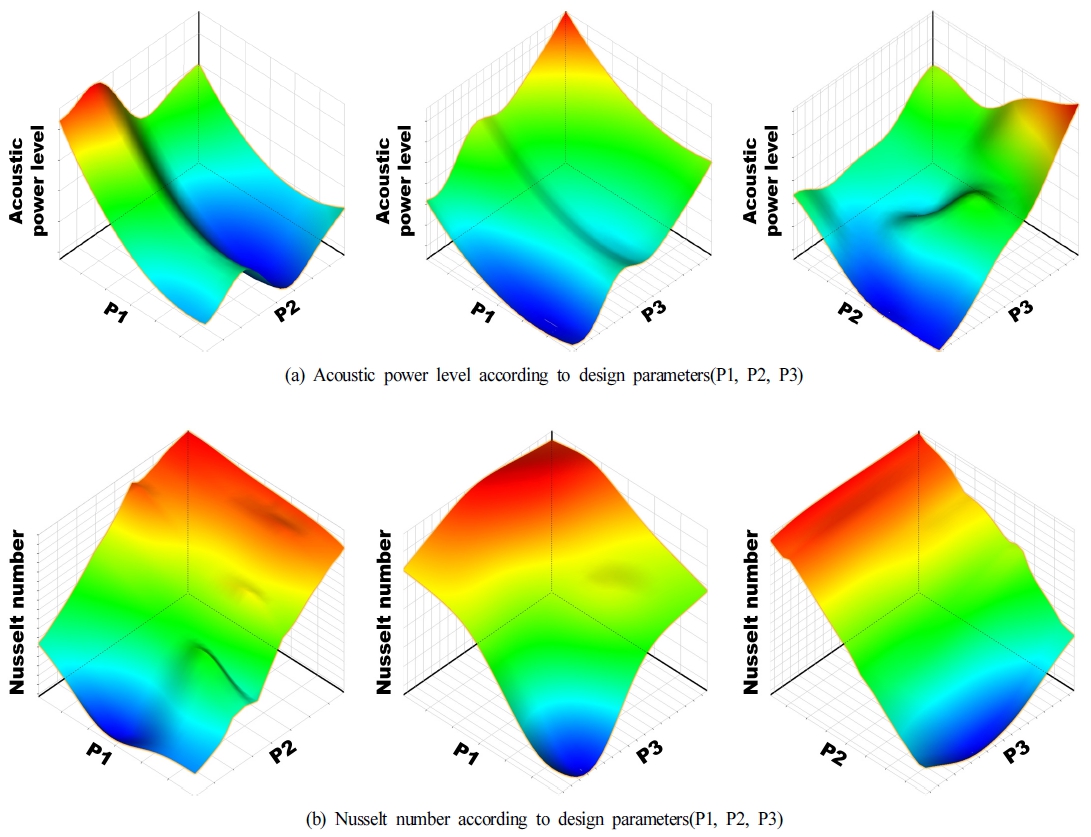
목적함수에 대한 설계변수의 민감도를 분석하기 위해 반응표면을 생성하였다. 세 가지 설계변수(P1, P2, P3)가 목적함수인 Nu 수와 음향 출력레벨에 미치는 영향을 분석하였으며, Fig. 4에 도시하였다.
방열성능을 비교하기 위한 지표로 사용된 Nu 수는 덕트의 후단부 길이를 의미하는 설계변수인 P2의 영향도가 가장 지배적임을 알 수 있다. P2의 길이가 줄어들수록 평균 Nu 수는 높아지는 경향을 보였다. 또한, 설계변수에 대한 음향 출력레벨은 P2와 P3에서 공통적으로 민감하게 변화하였다. 하지만, Nu 수와 같이 단방향 경향성을 보이지 않고, 특정 지점에서 음향 출력레벨이 높거나 낮은 특징을 보였다. 따라서, 덕트의 설계변화에 따른 음향 출력레벨은 특정 최적점이 있음을 유추할 수 있다.
반응표면 내의 최적점을 선정하기 위해 문제에 대한 해답을 무작위로 생성하여 선택(selection), 교차(crossover), 돌연변이(mutation)를 주요 연산으로 진화시켜 해답을 찾아가는 유전 알고리즘(genetic algorithm)이 사용되었다. 라디에이터 홴에서 발생되는 유동소음과 방열성능을 동시에 고려하기 위해 다목적 유전 알고리즘(multi-objective genetic algorithm; MOGA) 기반의 예측모델을 생성하였다. 덕트 형상을 결정하는 설계변수에 대한 최적설계를 통해 3 mm의 폭 (P1), 80 mm와 6.5 mm의 전단 및 후단(P2, P3) 길이의 덕트가 설계되었다.
3.4 최적설계
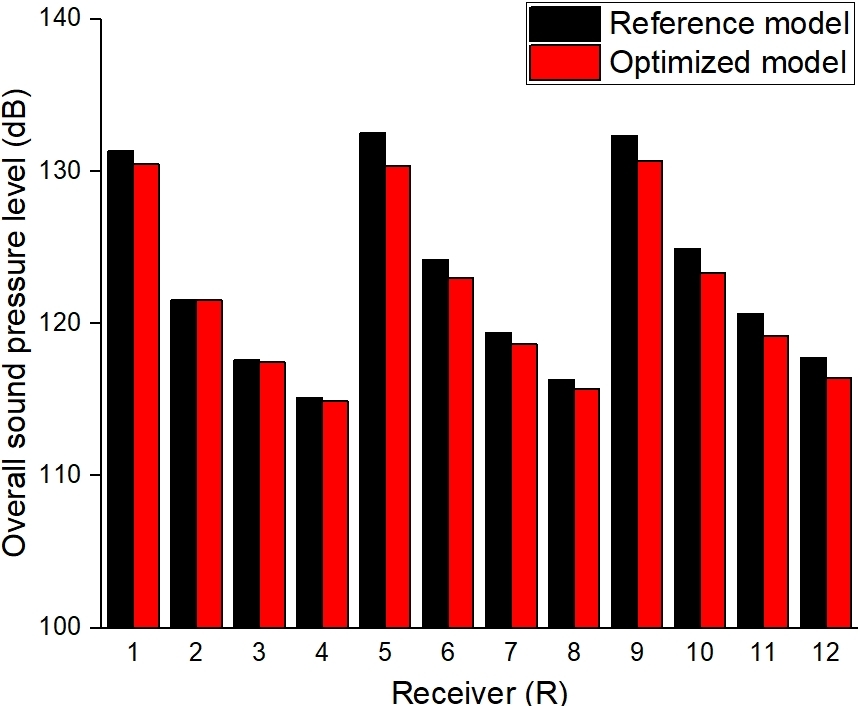
음향 출력레벨을 목적함수로 설정한 최적설계 결과를 검증하기위해 Table 2의 12가지 청취자 위치에 대한 overall sound pressure level(OASPL)을 계산하였다. OASPL은 다양한 주파수에 대한 음향 출력레벨의 적분형이며, 청취자가 듣게되는 종합적인 소음의 세기로 고려될 수 있다. 기존 모델과 최적화된 모델의 OASPL은 청취자 위치에 따라 Fig. 5와 같이 계산되었다. 형상은 X축을 기준으로 대칭구조이기 때문에 유사한 크기의 소음이 계산되었으며, 일부 청취자 위치인 R2∼R4에서 최적화 모델의 소음과 기존 모델의 소음이 유사한 크기로 계산되었다. 이는 최적화의 효율성을 위해 다양한 청취자를 고려하지 않고, 단순히 음압 변동만을 고려하여 최적화하였기 때문에 발생되는 타 소음원에 의한 영향으로 값이 미미하여 해당 모델을 사용하였다.
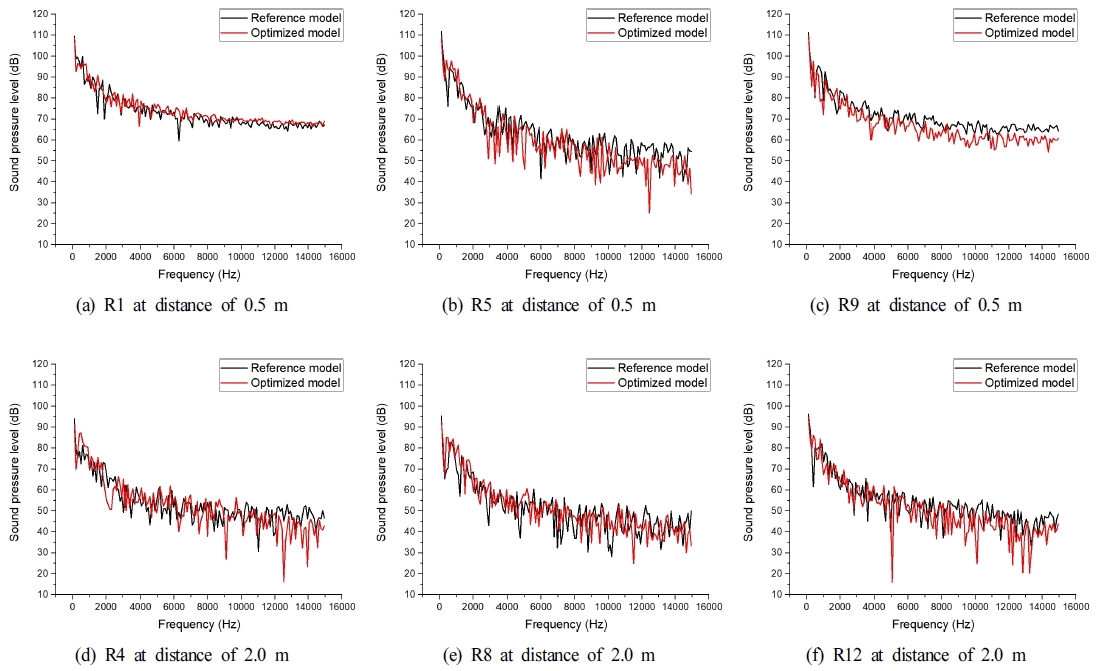
소음은 세기와 더불어 특성도 중요하게 고려되어야 한다. 개선설계로 인해 전체 소음과 더불어 어느 주파수 성분의 소음이 어떻게 변화하였는지에 따라 청취자가 느끼는 소음의 특징이 완전히 다를 수 있기 때문이다. 따라서, 소음 특성의 자세한 분석을 위해 청취자의 위치 중 가까운 거리인 R1, R5, R9와 먼 거리인 R4, R8, R12의 주파수 대역별 소음 특성을 분석하였다. 특정 주파수별 소음을 분석하기 위해 고속 푸리에 변환(fast Fourier transform; FFT)을 사용하였으며, 계산 결과는 Fig. 6으로 도시하였다.
소음원인 라디에이터 홴의 중심부와 0.5 m 떨어진 위치의 청취자 R1, R5, R9은 2.0 m 떨어져 위치하는 청취자 R4, R8, R12에 비해 소음저감 효과가 크게 계산되었다. 특히, 저주파 소음에 비해 고주파 소음의 감소폭이 크게 계산되었는데, 이는 청취자에게 불쾌한 주파수 영역의 소음으로 적절히 최적화되었다고 판단된다. 일반적으로, 같은 방향에 위치한 청취자는 비슷한 소음의 특성이 계산되며, 청취자 거리가 증가함에 따라 소음이 감소되는 경향을 확인할 수 있다. 먼 거리에 위치한 청취자 R4, R8, R12는 직접적인 음압 변동의 영향을 받지 않기 때문에 최적화로 인한 고주파 영역의 소음 감소폭이 미미하다. 하지만, 낮은 음압 변동으로 압력 차가 작은 특정 주파수에서는 기존 모델에 비해 소음의 감소폭이 크게 계산되었다. 라디에이터 홴 덕트의 최적설계를 통해서 소음은 최소 0.0234 dB에서 최대 2.148 dB로 감소되었다.
소음만을 고려하여 덕트가 설계될 경우 오히려 공기역학적 성능이 감소될 수 있다. 이에, 본 연구에서는 라디에이터 홴의 방열성능 향상을 만족하는 저소음 홴을 설계하고자 하였다. 소음은 음압 변동을 활용하여 예측 후 다양한 거리의 청취자에서 공력음향을 직접 계산하여 비교하였다. 라디에이터 홴의 방열성능을 분석하기 위해 일정 표면온도가 부여된 라디에이터 표면에 평균 Nu 수를 계산하였다. 기존 모델의 라디에이터를 표현하는 열원부의 평균 Nu 수는 약 4,730로 계산되었고, 최적화를 통해 도출된 모델의 면 평균 Nu 수는 약 4,853으로 계산되었다. 기존 모델 대비 약 2.54%로 미미하게 향상되었지만, 단순한 덕트 형상 개선으로도 방열성능을 향상시킬 수 있음을 알 수 있었다. 또한, 덕트 형상은 홴의 방열성능에 비해 소음에 더 지배적인 영향을 미친다는 것을 알 수 있었다.
4. 결 론
전기자동차 시장의 도래에도 높은 에너지 밀도를 가진 배터리의 열관리에 활발하게 사용되는 라디에이터 홴은 소음 문제가 중요하게 대두되고 있다. 홴 소음을 저감하기 위해서는 일반적으로 덕트가 사용되는데, 이는 오히려 공기역학적 성능을 저감시켜 방열성능에 악영향을 미칠 수 있다. 따라서, 본 연구에서는 방열성능과 소음을 모두 고려한 라디에이터 홴 덕트 최적설계 방안을 다음과 같이 정리하였다.
- 1) 수치 해석적 기법에 기반한 공력음향 연구는 일반적으로 많은 계산 비용과 시간을 수반한다. 형상과 상관없이 덕트 설계만으로도 저속 홴에 지배적인 소음원인 홀극자 소음을 크게 감소시킬 수 있다. 따라서, 본 연구에서는 정상상태 기반 유동해석을 활용하여 음압 변동을 계산 후 목적함수로 사용하였다.
- 2) 또 다른 목적함수로 라디에이터 방열성능을 확보하기 위해 Nu 수를 사용하였다. 라디에이터 표면의 일정 온도를 가정하여, 덕트 형상 최적화로 인한 대류 열전달을 비교하기 위해 평균 Nu 수를 계산하였다. 기존 홴으로 인한 라디에이터 표면 평균 Nu 수는 약 4,730로 계산되었으며, 최적설계된 홴에서는 약 4,853가 계산되었다. 단순한 덕트 형상 개선으로도 기존 모델 대비 약 2.54%의 Nu 수가 향상되었다.
- 3) 예측된 최적화 모델에 대해 공력음향을 계산하였다. 총 12개의 청취자 위치에서 계산하였으며, X축 방향 일부 2∼4 청취자 위치에서 최적화 모델의 소음이 기존 모델의 소음보다 높게 계산되었다. 이는 단순한 음압 변동만을 고려하여 최적화되었기 때문에 음압 변동으로 계산되지 않는 다른 소음원의 영향으로 사료된다.
- 4) 먼 거리의 청취자에 비해 가까운 거리의 청취자에서 음압 변동을 활용한 최적화로 인해 소음저감 효과가 크게 계산되었다. 일반적으로, 같은 방향에 위치한 청취자는 비슷한 특성의 소음이 계산되었다. 먼 거리에 위치한 청취자는 직접적인 음압 변동의 영향을 받지 않기 때문에 최적화로 인한 고주파 영역의 소음 감소폭이 미미하게 계산되었다. 최적설계로 인해 청취자 위치에 따라 최소 약 0.023 dB에서 최대 약 2.148 dB 감소되었다.
- 5) 본 연구를 통해 덕트를 활용하는 홴 설계의 경우 정상상태 유동해석에 기반한 광대역 소음원 모델을 활용하여 소음저감 설계를 수행할 수 있음을 제시하였다. 하지만, 소음의 크기 및 특징을 정확히 분석하기 위해서는 음향 상사법에 기반한 다양한 공력음향 방정식을 계산할 필요가 있다. 또한, 홴 등과 같은 저속 회전기계에서는 공력음향과 더불어 모터의 주파수 간섭 등을 받기 때문에 함께 고려할 필요가 있다고 사료된다.
References
- Persistence Market Research, 2020, “Global Market Study on Automotive Radiators,” Automotive Radiator Market.
-
Wiebelt, A., and Zeyen, M. G., 2018, “Battery Thermal Management,” Springer.
[https://doi.org/10.1007/978-3-662-53071-9_13]

-
Kilinc, F., Buyruk, E., and Karabulut, K., 2020, “Experimental Investigation of Cooling Performance with Graphene Based Nano-Fluids in a Vehicle Radiator,” Heat and Mass Transfer, Vol. 56, pp. 521∼530.
[https://doi.org/10.1007/s00231-019-02722-x]

-
Zhang, T., Gao, Q., Gu, Y., and Li, Y., 2021, “Studies on Thermal Management of Lithium-Ion Battery Using Non-Metallic Heat Exchanger,” Applied Thermal Engineering, Vol. 182, No. 5, 116095.
[https://doi.org/10.1016/j.applthermaleng.2020.116095]

- Jain, S., and Deshpande, Y., 2012, “CFD Modeling of a Radiator Axial Fan for Air Flow Distribution,” World Academy of Science, Engineering and Technology, Vol. 6, pp. 1058∼1063.
- Sulaiman, M. Y., Azraai, S. B., and Abdullah, W. M. W., 2009, “CFD Modeling of Air Flow Distribution from a Fan,” ICADME, Batu Ferringhi, Penang, Malaysia, 1B.
-
Nashimoto, A., Akuto, T., Nagase, Y., Yoda, T., Nakano, T., and Fujisawa, N., 2007, “Detection of Aerodynamic Noise Sources over a Rotating Radiator Fan Blade for Automobile,” Journal of Passenger Cars: Mechanical System Journal, Vol. 116, pp. 396∼401.
[https://doi.org/10.4271/2007-01-0545]

-
Suzuki, A., and Soya, A., 2005, “Study on the Fan Noise Reduction for Automotive Radiator Cooling Fans,” SAE Technical Paper 2005-01-0601.
[https://doi.org/10.4271/2005-01-0601]

-
Yoshida, K., Semura, J., Kohri, I., and Kato, Y., 2014, “Reduction of the BPF Noise Radiated from an Engine Cooling Fan,” SAE Technical Paper 2014-01-0631.
[https://doi.org/10.4271/2014-01-0631]

-
Sriwijaya, R., Anjasmoro, I., Akmal, M., Yoga, G. P., and Purwanto, T. P., 2019, “Noise Reduction of Passenger Vehicle Radiator Cooling Fan by Utilizing Additional Plates and Damping MAterials,” AIP Conference Proceedings 2187, 050017.
[https://doi.org/10.1063/1.5138347]

-
Gerard, A., Moreau, S., Berry, A., and Masson, P., 2015, “Design of Multi-Modal Obstruction to Control Tonal Fan Noise Using Modulation Principles,” Journal of Sound and Vibration, Vol. 356, No. 10, pp. 34∼47.
[https://doi.org/10.1016/j.jsv.2015.06.003]

-
Cao, C., Zhao, G., Zhao, Q., and Wang, B., 2021, “Numerical Investigation and Optimization for Interior Duct Shape of Ducted Tail Rotor,” Aerospace Science and Technology, Vol. 115, 106778.
[https://doi.org/10.1016/j.ast.2021.106778]

- Tata Motors, 2022, http://www.tatamotors.com/, .
-
Lighthill, M. J., 1952, “On Sound Generated Aerodynamically. I. General Theory,” Proceedings of the Royal Society of London, Series A, Mathematical and Physical Sciences, Vol. 211, No. 1107, pp. 564∼587.
[https://doi.org/10.1098/rspa.1952.0060]

-
Ffowcs Williams, J. E., and Hawkings, D. L., 1969, “Sound Generation by Turbulence and Surfaces in Arbitary Motion,” Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, Vol. 264, No. 1151, pp. 321∼342.
[https://doi.org/10.1098/rsta.1969.0031]

-
Nicoud, F., and Ducros, F., 1999, “Subgrid-Scale Stress Modelling Based on the Square of the Velocity Gradient Tensor,” Flow, Turbulence and Combustion, Vol. 62, No. 3, pp. 183∼200.
[https://doi.org/10.1023/A:1009995426001]