Effect of Air Injection Holes Intrusiveness on Internal flow Phenomena of a Draft Tube Inside a Francis Turbine Model

1. Introduction

Part load (PL) conditions are designated by lower flowrate (Q) operating conditions. The downstream swirl instabilities at this condition contribute to the higher losses in the draft tube (DT).⁽¹⁾ Because of the significant runner exit circumferential velocity at PL condition, a helical precessing vortex is generated called vortex rope. In the runner rotation direction, these vortex ropes rotate with a precession frequency of about 0.2 to 0.4 times the rotational frequency of the runner.⁽²⁾ The vortex rope is a significant contributor to the DT flow instabilities which are responsible for vibration and pounding noise.⁽³⁾ The turbine may fail catastrophically because of the DT surge when the vibrational frequency matches the natural frequency of the structure.

In the Francis turbine cavitation is a very common phenomenon that results in noise and vibration in the draft tubes. At PL condition cavitation can take place inside t he v ortex rope which further increases the amplitude of the pressure fluctuations at the DT wall. Hence the turbine may fail due to resonance as well as due to pitting of the material.⁽⁴⁾

The nature of the DT flow induces the low-frequency instabilities which disrupt the stable and safe operation of the turbine so, to suppress this DT surge various techniques have been developed. There are three main control approaches for dealing with the pressure changes caused by the cavitating vortex rope; stabilizer fins mounted on the DT wall, air or water injection, and runner cone extension.⁽⁵⁾ These strategies have virtues in terms of reducing the surge, but they also have flaws. Given other physical design restrictions on turbines, extending the runner cone can be prohibitive. Insufficient air supply keeps the vortex rope unhindered and the natural frequency may decrease which leads to the resonance.⁽⁶⁾ Muntean et al.⁽⁷⁾ discovered that when the turbine works at a reduced discharge, the dynamic behaviour is severely harmed by the air injection control mechanism. Also, air or water admission frequently necessitates the use of more electricity.

Installing fins in the entrance cone of a draft tube is a popular method of reducing pressure surges. It is an intrusive type of mitigation strategy which decreases the high swirl content in the outlying zone of the DT since it is mounted on the DT circumference parallelly in the flow direction. Nishi et al.⁽⁸⁾ used wall pressure pulses to evaluate the influence of fins on the half load surging and suggested that triangular fins are more effective than square ones. Mounted fins, on the other hands, were discovered to be prone to significant efficiency losses, cavitation erosion, and the ability to enhance structural vibrations.

Taking into account the combination of characteristics, some researchers used both fins and air admission approaches, called hybrid control, to alleviate the draft tube surge.(^9,10) In this hybrid control, holes on the surface of a fin or on the runner crown are used to allow air in. Kim et al.⁽¹⁰⁾ investigated numerically the effect of anti-swirl fins along with air injection from runner crown for which they considered four fins. Cylindrical holes are protruded from the surfaces of the fins inside the DT in their model. At PL condition without considering cavitation, they discovered that the control methodology significantly reduces the pressure pulsation and the operation range is broadened for the Francis turbine. But, the intrusion portion of the injection holes obstructs the incoming flow and some complex flow phenomenon takes place which was not elaborated by the researchers.

Conclusively, the utilization of fins along with the air injection technique greatly mitigate the DT synchronous pressure pulsations. The obstruction created by the injection holes in the DT flow induces flow complexity and randomness near the hole surface which could be detrimental to the safe working of the Francis turbine. Therefore, a thorough investigation is needed for the explanation of the physics behind these complex flows. To address this important issue of the control techniques, the current study investigates numerically the effect of air injection hole protrusion inside the DT on the pressure pulsation. The operating condition is selected at PL condition with cavitation for the same geometrical model used by Kim et al.⁽¹⁰⁾. The anti-swirl fins with and without air injection holes are considered for the study but the air injection technique is not taken into account. A transient numerical investigation is carried out for the accurate prediction of the flow complexities. The experimental investigation is also performed for the numerical validation.

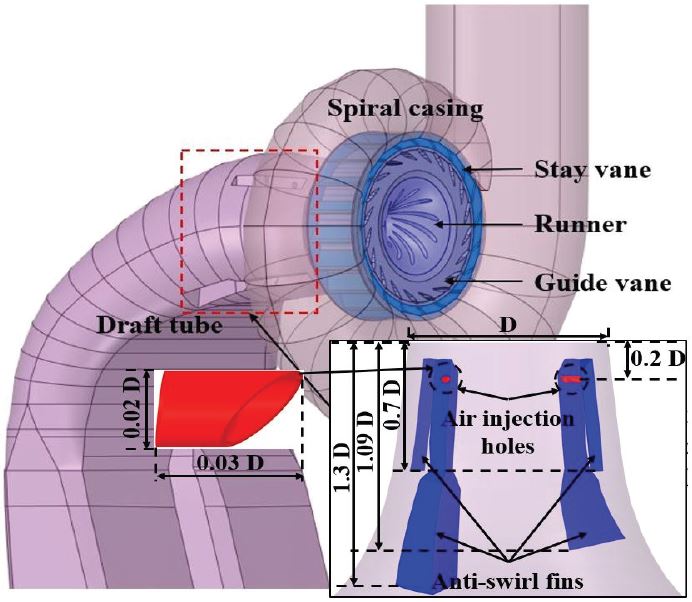
2. Geometrical model

The present numerical study utilizes the three-dimensional (3-D) geometry of the Francis turbine model. The turbine model consists of stationary components; spiral casing, stay vanes, guide vanes and a draft tube as well as rotating component; runner. The basic function of the draft tube is to guide the runner exit flow and convert the excess kinetic energy (KE) into static pressure. The DT has two diffusers for better conversion. The full geometrical model is shown in Fig. 1 in which a zoomed-in view of the anti-swirl fins is also depicted. There are four fins mounted on the DT out of which two are long fins placed opposite to each other and two fins are short fins that are also placed diagonally. At each fin, one air injection hole (red colour in Fig. 1) is generated which is protruded inside the DT and acts as an obstruction in the flow. The holes are situated at a location of 0.09 D₂ from the DT inlet. In general, the flow gets obstructed by the fin’s geometry but due to the intrusive nature of the holes the incoming flow gets more deflected and flow exhibits unsteadiness near the holes.

Fig. 1

3D geometrical model of the Francis turbine

The operating condition for the turbine is set at a lower flowrate for which Q/Q_BEP=0.74 (BEP-Best efficiency point) that lies between the range of flowrate which exhibits severe downstream instabilities. For the cavitating vortex rope, cavitation condition is also incorporated in this study. The cavitation phenomenon is quantified by a non-dimensional quantity called Thoma number (σ). The σ depends on the suction head of the turbine, so by regulating pressure at the DT outlet, the suction head is created for which the cavitation initiates. This condition is termed cavitation inception and the value of σ=0.266 in the current investigation. Hence, the pressure pulsation with and without holes is transiently investigated at PL condition with cavitation inception point. The specifications of the Francis turbine model are tabulated in Table 1. The coefficients definitions in Table 1 can be referenced in ref.⁽¹¹⁾

Table 1

Turbine specifications and operating conditions

3. Numerical methodology

The internal flow physics is predicted using the commercial software ANSYS CFX in the present numerical study. Since the flow in the turbine is turbulent and transient in nature, the physics of this flow is captured by solving unsteady Reynolds averaged Navier Stokes (URANS) equations assuming the flow is incompressible. The closure problem of the URANS equations is treated by the scale adaptive simulation shear stress transport (SAS-SST) model which precisely captures the vortical flows in the Francis turbine.⁽¹²⁾ To model the cavitation a widely accepted two-phase Rayleigh-Plesset model is employed.⁽¹³⁾ The numerical solution needs discrete points so grids are generated on the turbine model. For spiral casing and DT, a tetrahedral mesh is generated while for other components hexahedral mesh is employed. The runner is a spinning component so the y⁺ value for this is kept below 5. The mesh independency is handled by a technique called Grid c onvergence i ndex (GCI) f or which three meshes are generated; fine, medium and coarse.⁽¹⁴⁾ For these meshes discretization errors are calculated. For fine mesh with 8.95×10⁶ grid elements, the GCI values of efficiency and flowrate are 0.0091 and 0.0093. Since these values are below 0.01 so the fine mesh is considered for further investigations. The generated grids on the turbine model are depicted in Fig. 2.

Fig. 2

Computational grid on the turbine model

The physical components of the turbine are merged with the interfaces. The rotating and stationary domains are connected with General Grid Interface (GGI). The boundary conditions are specified in Table 2. The boundary condition for the inlet of the spiral casing is mass flow rate and the static pressure is applied at the DT outlet for the cavitation inception. No-slip and automatic wall functions are applied at the turbine’s wall. The unsteady cavitating flow is solved by initializing the solutions by steady cavitating solutions which are also initialized by steady non-cavitating solutions. Hence, the transient investigation has better convergence. The time step is calculated for the 1.5° of runner rotation and five full runner revolutions are considered for the solution.

Table 2

Boundary conditions

4. Results and discussions

4.1 Numerical validation

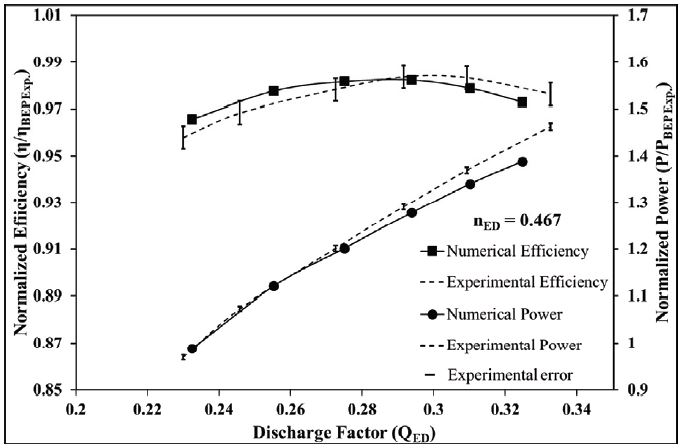
The developed numerical methodology for the Francis turbine model is validated with the experimental data which is obtained from the IEC 60193 standard based experimentation. For the verification of performance characteristics of the turbine, steady results are utilized at n_ED=0.467 with the variation of guide vane openings from 16° to 26°. The experiment is performed on the model having anti-swirl fins with air injection holes. Figure 3 shows the validation of efficiency and power and these are in good agreement with the experimental results. The efficiency and power are normalized using the BEP values of the experiment.

Fig. 3

Performance validation of the turbine model

4.2 Unsteady hydraulic performance

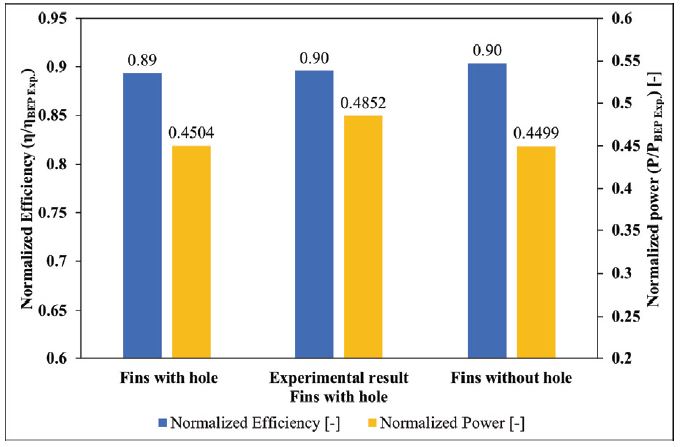
To analyse the effect of air injection hole protrusion on the hydraulic performance, efficiency and power are calculated using the unsteady methodology for with and without holes cases. At PL with cavitation inception point, the numerical and experimental performance curves are depicted in Fig. 4. The experimental results are obtained for the turbine which has holes protruded on its DT. The efficiency and power are non-dimensionalized using the ex perimental B EP r esults. With h oles o n the fin’s surfaces, the numerical performances are in good agreement with the experimental results as shown in Fig. 4. Because of the smoother flows near the fins, the efficiency attains an increased value for the DT without air injection holes compared to with holes case. However, the numerical power for both cases shows insignificant variation.

Fig. 4

Performance characteristics of the turbine model

In order to justify the efficiency increment in the without holes case, the DT head loss is calculated for both the cases using eq. (1).⁽¹⁰⁾

$\[ H_{loss}=\frac{△p}{\rho g} \]$

(1)

where △p is the pressure difference between inlet and outlet of the draft tube domain, ρ is the density of the fluid and g is the gravitational acceleration. The loss percentage is calculated by normalizing the head loss by the effective head at PL condition. It is found that for the DT having fins with air injection holes, the head loss is 9.34% while the DT without holes exhibits l esser head loss of 8 .8%. Hence, it i s clear that the hole’s protrusion creates more flow complexities with unsteadiness which contribute to the efficiency reduction.

4.3 Internal flow phenomena

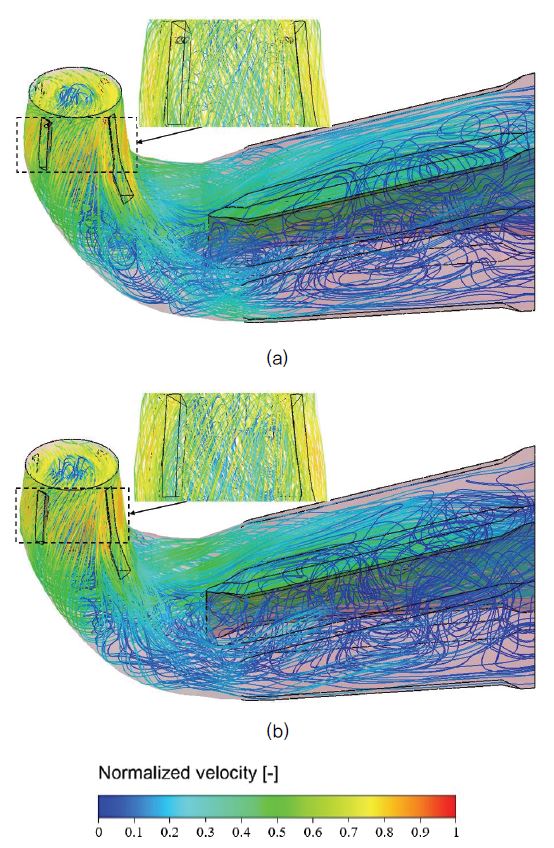
The evaluation of complex internal flow characteristics of the turbine model is essential for the prediction of the effect of the air injection hole protrusion. The accurate flow field visualization is obtained through velocity streamlines for both the cases as shown in Fig. 5. The plots are obtained by averaging the velocity for the last two runner revolutions and then normalized by the maximum velocity. It can be observed from Fig. 5 that the DT with and without holes attain almost a constant velocity value. However, near the holes a slight increase of velocity can be seen in Fig 5(a) with flow non-uniformity compared to without holes case in Fig 5(b). The recirculating flow has occurred for both the cases at the DT centre resulting in the vortex rope generation. The circumferential momentum pushes the flow towards the larger curvature of the elbow of the DT. Improper kinetic energy conversion is achieved at this operating condition caused by the PL vortex rope and cavitation for both cases. Thus, hole protrusion causes more non-uniformity near the holes which plays a role in the improper energy conversion.

Fig. 5

Velocity streamline distributions (a) Fins with holes (b) Fins without holes

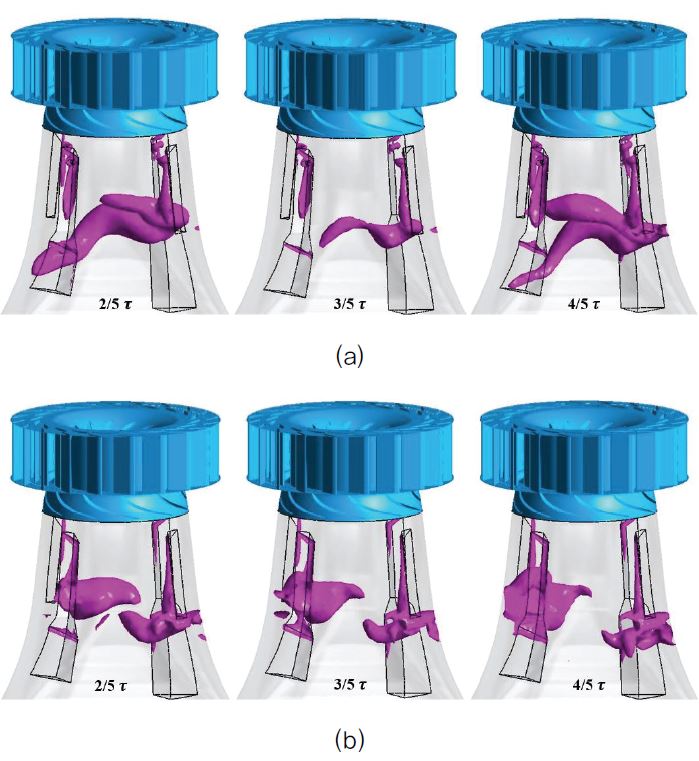
The cavitating vortex rope inside the DT can induce large pressure fluctuations and the operating range of the turbine is minimized. So, in the present study accurate p rediction of t he v ortex rope is p resented through Iso-surface distribution of pressure which is shown in Fig. 6. The Iso-surfaces are plotted for three instants (τ) during the last runner revolution. The boundary-value of pressure for these plots is set at the saturation pressure (p_sat) of the water. From this figure, a large vortex rope can be observed inside the DT with air injection holes at the fin’s surface. A significant reduction in t he v ortex rope strength i s obtained for the without holes case. The precession direction of the vortex rope is the same as that of the runner’s rotational direction. A low-pressure zone is found for both the cases which are attached to the upper part of the fins at all the instants. Because of the increased velocity near the holes, the area of this low-pressure zone is increased which contributed to the complex flows near the holes while without holes case does not show such adverse characteristics. Overall, longer and wider vortex rope is induced with holes compared to without holes case. Hence, the swirl instabilities are comparatively enhanced.

Fig. 6

Iso-surface distribution of pressure (p=psat) (a) Fins with holes (b) Fins without holes

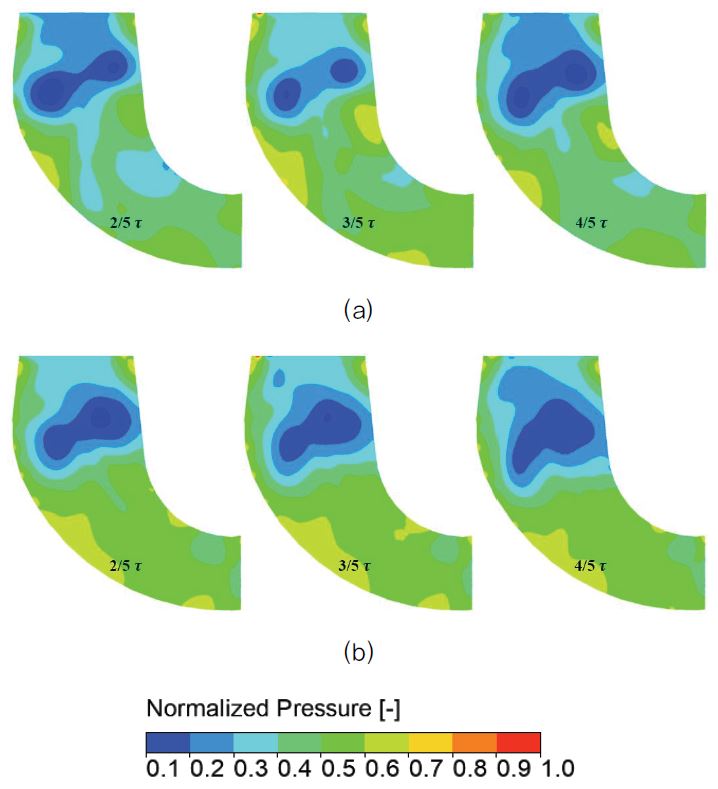
The static pressure contours inside the DT are also plotted at the mid-section for three instances to validate the vortex rope plots in Fig. 7. The pressure is normalized using maximum pressure and the lowest pressure value corresponds to the saturation pressure of the water. It can be noted from Fig. 7 that the low pressure occurs for both the cases in the form of random lobes because the vortex rope is non-uniform across the mid-section of the DT (Figure 6). Draft tube with hole exhibits higher area for low-pressure zone compared to without holes case which is indicative of increased downstream instabilities. The lower pressure zones are entrapped in the cone portion of the DT so the induced flow complexities are more in this area only.

Fig. 7

Static pressure contours at the mid-section of DT (a) Fins with holes (b) Fins without holes

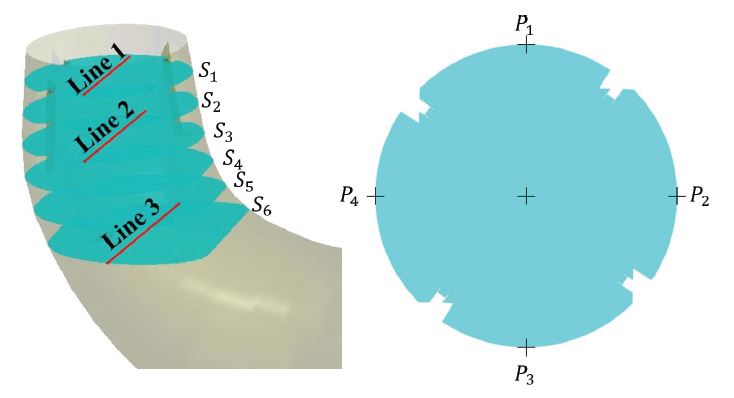
4.4 Swirl strength and pressure fluctuations

The swirl strength and pressure fluctuations are an important integral for the thorough investigation of the PL and cavitation induced instabilities. Figure 8 shows the monitoring points, lines and planes for which these parameters are calculated. There are six planes (S1 to S6) in the DT flow direction and at each plane, four points (P1 o P4) on the DT wall are monitored. The swirl intensity is represented using a non-dimensional number called swirl number (S) which is mathematically represented by eq. (2) and the unknowns notations can be found in ref.⁽¹⁰⁾;

Fig. 8

Monitoring points, line and planes

$\[ S=\frac{{\int }_0^R C_m\cdot C_u\cdot r^2\cdot dr}{R{\int }_0^R C_m^2\cdot r\cdot dr} \]$

(2)

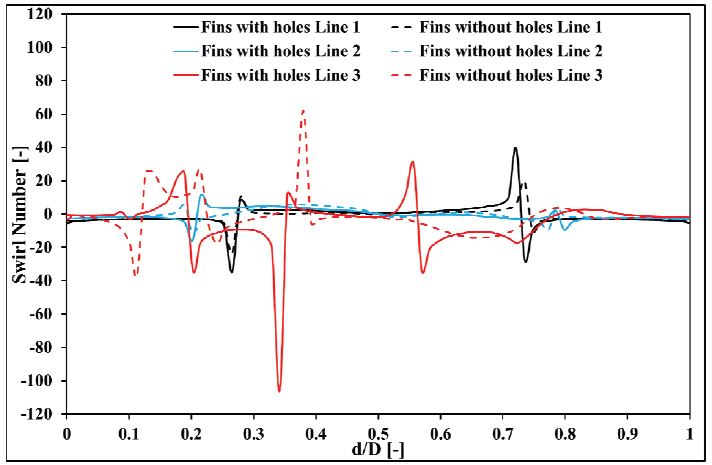
The swirl number is calculated at line 1, line 2 and line 3 which lie on the planes S₁, S₃ and S₆ respectively using statistical averaged circumferential and axial velocities as shown in Fig. 9. In this figure, 0 and 1 denote two opposite points on the DT circumference. Since the vortex rope is not regular, the swirl number is also showing the same behaviour. The variation in the swirl number can be seen at two points which are on either side of the DT centre. The DT without air injection holes is clearly showing lesser swirl strength compared to the DT with holes for all the lines in the flow direction.The maximum swirl intensity is obtained at line 3 as the axial component of the velocity becomes very low in the downstream direction of the DT. The decrement in the maximum values of the swirl number for without holes case is about 40.29%, 25.26% and 41.66% at lines 1, 2 and 3 respectively. Hence, the hole protrusion significantly increased the swirl intensity which further reduce the working range of the Francis turbine.

Fig. 9

Swirl number at Line 1 inside the DT

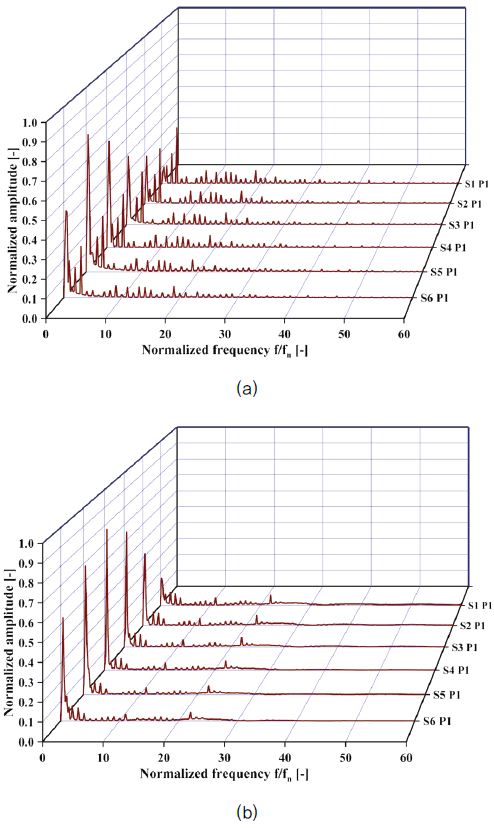
The pressure fluctuations are essential for the design point of view of the turbine. Fast Fourier transforms (FFT) methodology is employed to calculate the pressure pulsations on the DT wall at PL and cavitation inception point as shown in Fig. 10. The pressure amplitudes are obtained at P₁ since maximum fluctuations occur at this point only. The amplitude is normalized using the maximum value during the calculation and the frequency (f) is normalized using runner rotational frequency (f_n). The PL caused vortex rope generally induces low-frequency pressure fluctuations. From Fig. 10(a) for the DT with holes, the low-frequency pressure peak can be observed at each point in the DT flow direction. These pressure peaks occur for the frequency range of 0.2 to 0.4 f_n. Apart from the low-frequency peak, a random pressure peak is obtained at 3 f_n beyond which the pressure pulsations are showing the normal trend. As the holes are removed from the fin’s surface, this random pressure fluctuation is significantly suppressed as shown in Fig. 10(b). However, a slight increase in the low-frequency peak can also be observed from this figure. Therefore, it is proved that the random pressure pulsation at 3 f_n occurs due to the presence of air injection holes protrusion inside the DT due to which the turbine’s operating range is limited.

Fig. 10

Pressure pulsations (a) Fins with holes (b) Fins without holes

5. Conclusion

The present study investigates the effect of protrusion of air injection holes in the DT flow which are attached to the fins. These holes obstruct the incoming f low and induce some random complex ities. The accurate calculations of the performances and internal flow characteristics of the turbine with and without holes are performed using the unsteady numerical methodology. The effect of these holes was investigated at PL condition incorporating the cavitation inception point at σ=0.266. It was found that the protrusion of the air injection holes reduces the efficiency by about 1% compared to the without holes case by creating some complex flows near the holes. The non-uniformity caused by these holes is the result of longer and wider vortex rope which is minimized by removing the holes. Also, significant low-pressure zones are attached to the fin’s holes which are reduced for the case of without holes. The maximum swirl intensity inside the DT is reduced by about 41% for the DT without holes which will lead to the stable operation of the turbine. Finally, random pressure pulsations at a higher frequency are the results of the hole’s protrusion which is remarkably suppressed for without holes case. Furthermore, this study can be utilized for the optimization of the holes and fin’s shape.

Acknowledgments

This research was funded by the Korea Agency for Infrastructure Technology Advancement under the Ministry of Land, Infrastructure, and Transport (grant number 22IFIP-C128598-06) and partially funded by a grant (No. EM220003) from the Korean Institute of Industrial Technology (KITECH).

References

• H. Foroutan and S. Yavuzkurt, “Unsteady numerical simulation of flow in draft tube of a hydroturbine operating under various conditions using a partially averaged Navier-Stokes model,” J. Fluids Eng. Trans. ASME, vol. 137, no. 6, 2015. [https://doi.org/10.1115/1.4029632]
• C. Nicolet, A. Zobeiri, P. Maruzewski, and F. Avellan, “On the upper part load vortex rope in Francis turbine: Experimental investigation,” IOP Conf. Ser. Earth Environ. Sci., vol. 12, no. March 2016, p. 012053, 2010. [https://doi.org/10.1088/1755-1315/12/1/012053]
• H. Grein, “Vibration Phenomena in Francis turbines: their causes and prevention.,” Proceedings of 10th IAHR Symposium, Escher Wyss News, vol. 54–55, no. 1, 1981.
• P. P. Gohil and R. P. Saini, “Effect of temperature, suction head and flow velocity on cavitation in a Francis turbine of small hydro power plant,” Energy, vol. 93, pp. 613–624, 2015. [https://doi.org/10.1016/j.energy.2015.09.042]
• R. Zhang, A. Yu, M. Nishi, and X. Luo, “Numerical Investigation of Pressure Fluctuation and Cavitation inside a Francis Turbine Draft Tube with Air Admission through a Fin,” J. Phys. Conf. Ser., vol. 1909, no. 1, 2021. [https://doi.org/10.1088/1742-6596/1909/1/012017]
• X. Zhou, H. G. Wu, and C. Z. Shi, “Numerical and experimental investigation of the effect of baffles on flow instabilities in a Francis turbine draft tube under partial load conditions,” Adv. Mech. Eng., vol. 11, no. 1, pp. 1–15, 2019. [https://doi.org/10.1177/1687814018824468]
• X. Luo, A. Yu, B. Ji, Y. Wu, and Y. Tsujimoto, “Unsteady vortical flow simulation in a Francis turbine with special emphasis on vortex rope behavior and pressure fluctuation alleviation,” Proc. Inst. Mech. Eng. Part A J. Power Energy, vol. 231, no. 3, 2017. [https://doi.org/10.1177/0957650917692153]
• S. Muntean, R. F. Susan-Resiga, V. C. Cǎmpian, C. Dumbrava, and A. Cuzmoş, “In situ unsteady pressure measurements on the draft tube cone of the francis turbine with air injection over an extended operating range,” UPB Sci. Bull. Ser. D Mech. Eng., vol. 76, no. 3, 2014.
• M. Nishi, X. M. Wang, K. Yoshida, T. Takahashi, and T. Tsukamoto, “An Experimental Study on Fins, Their Role in Control of the Draft Tube Surging,” in Hydraulic Machinery and Cavitation, 1996. [https://doi.org/10.1007/978-94-010-9385-9_92]
• S. J. Kim, Y. Cho, and J. H. Kim, “Effect of air injection on the internal flow characteristics in the draft tube of a francis turbine model,” Processes, vol. 9, no. 7, 2021. [https://doi.org/10.3390/pr9071182]
• International Electrotechnical Commission. Hydraulic Turbines, Storage Pumps and Pump-Turbines–Model Acceptance Tests; Standard No. IEC 60193; IEC: Geneva, Switzerland, 2019.
• S. J. Kim, Y. S. Choi, Y. Cho, J. W. Choi, J. J. Hyun, W. G. Joo, and J. H. Kim, “Effect of fins on the internal flow characteristics in the draft tube of a francis turbine model,” Energies, vol. 13, no. 11, 2020. [https://doi.org/10.3390/en13112806]
• P. J. Zwart, A. G. Gerber, and T. Belamri, “A two-phase flow model for predicting cavitation dynamics,” 5th Int. Conf. Multiph. Flow, no. January 2004, p. 152, 2004.
• I. B. Celik, U. Ghia, P. J. Roache, C. J. Freitas, H. Coleman, and P. E. Raad, “Procedure for estimation and reporting of uncertainty due to discretization in CFD applications,” J. Fluids Eng. Trans. ASME, vol. 130, no. 7, 2008. [https://doi.org/10.1115/1.2960953]