원심 압축기의 임펠러 마하수에 따른 공력성능 특성에 관한 수치해석적 연구

1. 서 론

높은 에너지를 보유한 압축 공기는 그 활용 범위가 넓고 이용 규모도 크다. 이러한 압축 공기를 양산하는 압축기 가운데 축의 회전을 통해 압축을 하는 부류를 터보 압축기라고 한다. 터보 압축기는 유동 방향에 따라 크게 축류형과 원심형으로 분류하고 그 중 원심 압축기는 원심 효과를 이용하여 유체에 에너지를 부가한다. 유동 방향이 심하게 굴절되기 때문에 비슷한 규모의 축류형보다 유량 범위가 작고 또한 비슷한 유량 범위의 축류형보다 효율도 낮다. 하지만 운전 유량 범위가 넓어 저유량 범위에서 축류형보다 안정된 운전이 가능하고 유동의 불균일이나 왜곡으로 인한 성능의 저하량이 작다. 게다가 상승되는 압력량이 현저하게 커서 고압의 압축공기를 효과적으로 양산할 수 있으며 제작이 용이해 소형화가 가능하여 국내 상황에서 개발과 제작이 적합하다. 국내의 압축기 시장은 상당히 거대하지만 기술 수준이 다소 높지 않아 고성능, 고효율의 압축기 설계 및 제작이 꾸준히 요구되고 있다.

실제로 압축기 공력 설계는 성능 예측, 유동 해석을 바탕으로 설계 변수에 대한 많은 축적된 경험과 압축기 내부의 각 요소에 대한 유동 특성의 포괄적인 이해를 필요로 하며, 이에 필요한 기술은 축적된 데이터베이스에 근거를 두고 이루어진다. 이러한 기반 위에서 요구되는 효율, 유량, 압력비, 형상 치수 제한 조건들을 만족시키는 최적의 압축기를 얻기 위해서는 먼저 대략적인 설계가 이루어진 후 압축기의 내부 유동장과 여러 손실을 고려한 상세 설계 및 설계된 압축기에 대한 시험 평가가 선행되거나 수치계산을 통한 성능 예측이 동시에 수행되어야 한다.

예비 설계 단계에서 신뢰할만한 성능 곡선을 예측하는 것은 중요하기 때문에 여러 가지 압축기 형상과 작동점에 대해 적용할 수 있는 경험식 및 손실 모델을 찾기 위해 많은 노력이 기울여져 왔다. 일반적인 접근방법으로 Swain⁽¹⁾과 Aungier⁽²⁾, Oh et al.⁽³⁾, Cumpsty⁽⁴⁾ 등이 1차원적 해석 방법을 제시하였으나 이는 상세한 형상 정보가 필요하고, 만족할만한 성능 곡선을 얻기 위해서는 모형 시험 평가에 대한 계수를 지속적으로 수정해야하며 경우에 따라서는 신뢰하지 못할만한 성능 곡선을 예측한다. 이를 보완하기 위해 Casey⁽⁵⁾등은 설계점에서 4가지 주요한 무차원 변수를 사용하여 기하학적 형상에 대한 정보 없이 성능 곡선을 예측하는 방법을 제시하였다.

수치해석은 원심 압축기 뿐만 아니라 펌프나 터빈 등 일반적인 회전 유체기계 내부 유동해석을 통한 성능 예측과 유동현상의 이해, 실험적인 연구가 힘든 영역에 대한 해석, 서지(Surge)에서 질식(Choke)까지의 유량 범위에 대한 예측 등 그 필요성이 확대되고 또한 실제로 응용되고 있다. 따라서 본 연구는 원심 압축기의 수치계산에 대한 신뢰성 향상을 위해 데이터베이스를 구축하고 공력 성능 및 유동 특성을 평가하기 위해서 수행되었다.

2. 압축기 모델 및 수치해석 방법

2.1 압축기 모델

본 연구에 사용된 원심 압축기는 산업용 공기압축기로서 Fig. 1과 같이 임펠러와 디퓨저, 볼류트로 구성되어 있다.

Fig. 2에서 보듯이 임펠러는 16개의 동일한 날개를 가지고 있고, 디퓨저에는 9개의 베인(Vane)이 장착되어 있다. 설계점으로는 임펠러 날개 회전 속도 마하수((Blade Mach number) M_u = 1.03, 유량계수(Mass flow rate coefficient) ϕ=0.132 이다.

Fig. 1

Three dimensional view of the centrifugal compressor

Fig. 2

Three dimensional view of the impeller and vane diffuser

2.2 수치해석 방법

전산해석은 상용 프로그램인 Ansys CFX 11.0을 사용하였으며, 임펠러와 디퓨저의 격자는 Turbo Grid를 , 볼류트는 ICEM을 이용하여 육면체 격자로 구성하였다. 단일 유로 해석을 위해 원주 방향 주기 조건을 적용하고 무차원 거리(y⁺)가 30~200의 영역에 첫 번째 격자가 위치되도록 격자계를 설정하였으며, 임펠러 입구와 디퓨저 출구에 각각 더미(Dummy)를 붙여 총 12 만개의 격자를 사용하였다. 전체 유로(Full passage) 해석을 위해서는 임펠러와 디퓨저, 볼류트를 해석 영역으로 사용하였고 마찬가지로 임펠러 입구와 볼류트 출구에 각각 더미를 붙여 총 220 만개의 격자를 사용하였다. 일반적으로 유동이 매우 복잡한 압축기 벽 근처 지역(Near wall region)에서는 상당히 조밀한 격자가 필요하다. 본 연구 수치해석에 사용한 표준 k-ε RANS 난류 모델은 벽근처 지역을 연결시켜주는 충분히 일반성을 가진 벽함수(Wall function)를 사용하여 이러한 비 경제성을 보완해 줄 수 있다. 벽법칙의 관계식은 압력구배가 없는 1 차원 유동(Couette flow)으로부터 얻어진 결과로써, 경계층의 박리(Separation)나 정체 구역에서는 정확한 예측이 쉽지는 않지만 일반적인 경우에 있어서 대체로 합리적인 결과를 보여준다.

Fig. 3

Comparison performance results of the test and CFD calculations at the volute exit

3. 수치해석 결과 검증

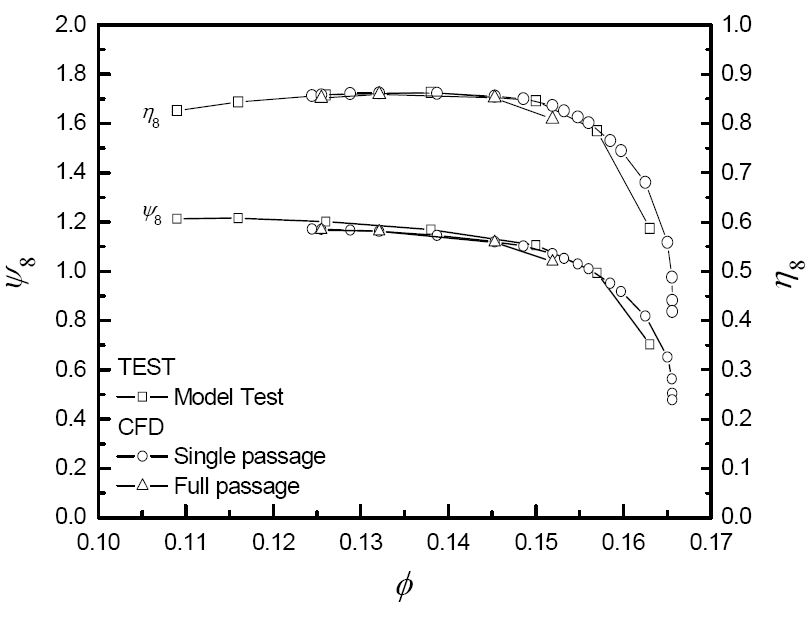
임펠러와 디퓨저, 볼류트 모두를 해석 영역으로 포함시켜 전체 유로 정상 해석을 수행하였고 마찬가지로 임펠러와 디퓨저의 단일 유로 정상 해석을 하였다. 또한 이를 축소된 모형 시험 결과와 비교하였다. Fig. 3에서 유량계수가 설계점인 0.132부근에서는 볼류트 출구까지의 압력계수(Head coefficient) 및 등엔트로피 효율(Isentropic efficiency)이 거의 일치하지만 탈 설계 구간에서는 전체 유로 해석이 시험 결과보다 성능을 다소 낮게 예측하고 단일 유로해석은 다소 높게 예측하는 것을 확인할 수 있다. 이는 단일 유로 해석의 경우 디퓨저 출구의 와류비(Swirl ratio)와 디퓨저-볼류트 출구의 면적비를 이용하여 비압축성 등 몇 가지 가정을 포함한 Japikse⁽⁶⁾모델의 볼류트 1차원 예측 결과와 전체 유로 3차원 수치해석 결과의 오차라 할 수 있겠다. 압축기 상세 설계와 성능 예측 관점에 있어서 단일과 전체 유로 해석은 설계점 근처에서 큰 오차가 없으며, 실험값을 잘 예측하는 것을 알 수 있다. 따라서 경제성을 고려하여 단일 유로 정상해석을 수행하더라도 합리적인 결과를 얻을 수 있다고 판단된다.

4. 해석 결과

4.1 압축기 전체 성능

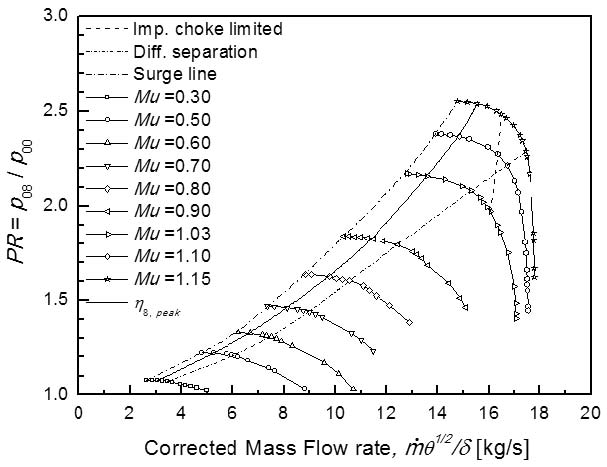
Fig. 4는 압축기 입구와 볼류트 출구 전압비를 유량으로 나타내었다. 유량이 적을 경우 비정상 유동 패턴을 확인 할 수 있는데 Compsty⁽⁴⁾나 Japikse⁽⁶⁾ 등의 문헌을 통해 일반적인 원심 압축기 시스템의 불안정성을 나타내는 서지는 성능 곡선에서 0 혹은 양의 기울기(∂PR/∂m)|N부근에서 존재하는 것을 알 수 있다.

실선으로 나타낸 최대 효율점(Peak efficiency)을 잇는 선을 따라서는 임펠러와 디퓨저 각 요소에서 그 유동 특성이 매우 유사하고, 최대 효율점은 설계점과 일치하며 경우에 따라 최대 효율점을 잇는 선을 작동선(Operating line)과 동일하게 간주할 수 있다.

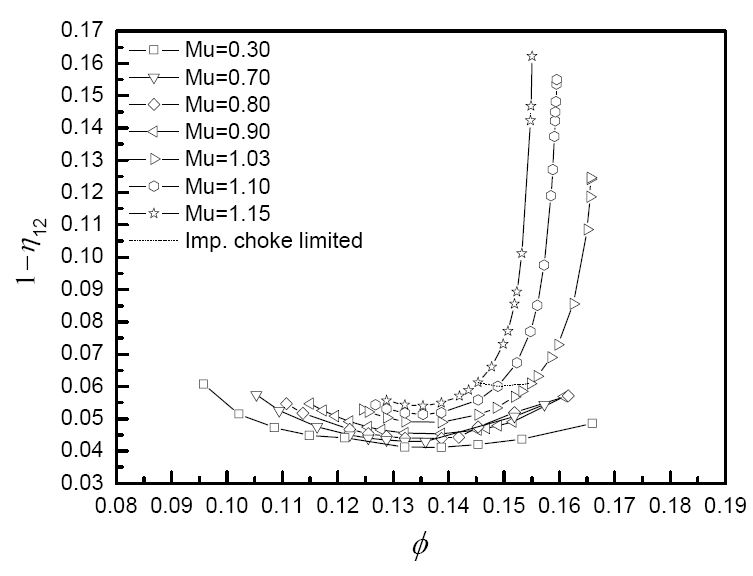
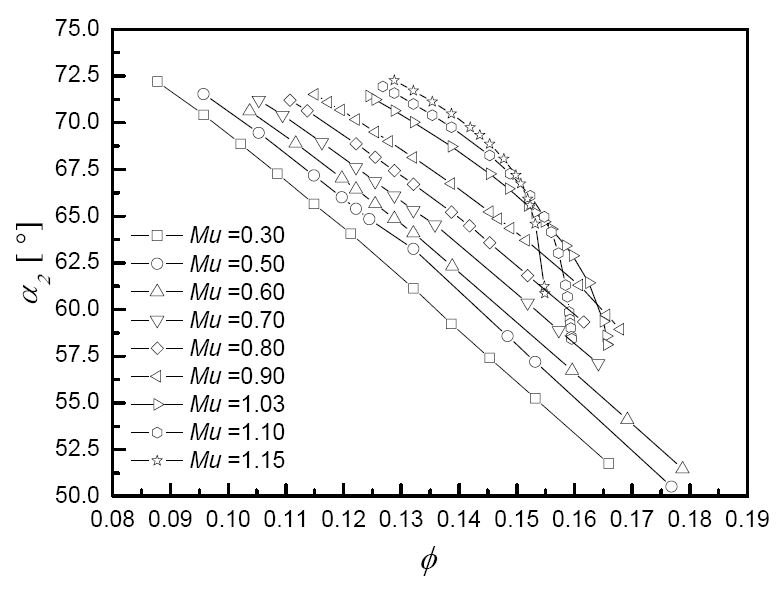
압축기 전체 성능에 대해 임펠러 날개 회전속도 마하수에 따라 고 회전속도(M_u = 1.03∼1.15)와 저 회전속도(M_u = 0.03∼0.90)로 유동 특성을 나눌 수 있다. 그 이유 중 하나는 디퓨저 박리(Separation)가 시작되는 선을 보면 알 수 있는데, 유량이 증가할수록 임펠러 출구에서 나오는 유동각 α₂ 가 작아짐에 따라 디퓨저 날개에 들어오는 입사각(Incidence) ι₃ 이 큰 음의 수를 가지면서 디퓨저 날개 압력면에 박리가 발달하여 디퓨저 성능을 현격하게 저하시키기 때문이다. 이 선은 유량계수(ϕ = 0.132)가 일정한 선과 M_u = 0.8에서 교차된다. ϕ = 0.132일 경우 저 회전속도에서는 디퓨저 박리가 진행되었기 때문에 현격히 낮은 성능을, 고 회전속도에 대해서는 최대 효율점 부근의 유량으로써, 높은 성능을 나타낸다. 디퓨저 박리 시작선은 질량유량, 입사각, 입구 마하수 등 몇 가지 변수를 통해 이를 예측할만한 경험식을 유도할 수 있을 것으로 판단된다.

두번째 원인으로서, 유량이 증가될 경우 임펠러, 디퓨저 각 목(Throat)에서 유량이 질식될 수 있다. 본 연구에 사용된 압축기는 임펠러에서 먼저 유량이 질식되고 그 후에 디퓨저에서 질식이 진행됨을 확인했다. 0.90 이하의 임펠러 날개 회전속도 마하수에서는 유량이 질식되지 않았으며 1.03 이상에서만 질식이 진행되었고, 이 특성은 질량유량, 입출구 단면적, 입구 밀도 및 전온도, 회전속도, 입사각 등 몇 가지 변수를 통해 선형적으로 예측할 수 있다고 판단된다.

Fig. 4

Performace map for variations of corrected mass flow rate and blade Mach number

4.2. 임펠러 내부 유동 특성

4.2.1 저 회전속도(M_u = 0.03∼0.90) 유동 특성

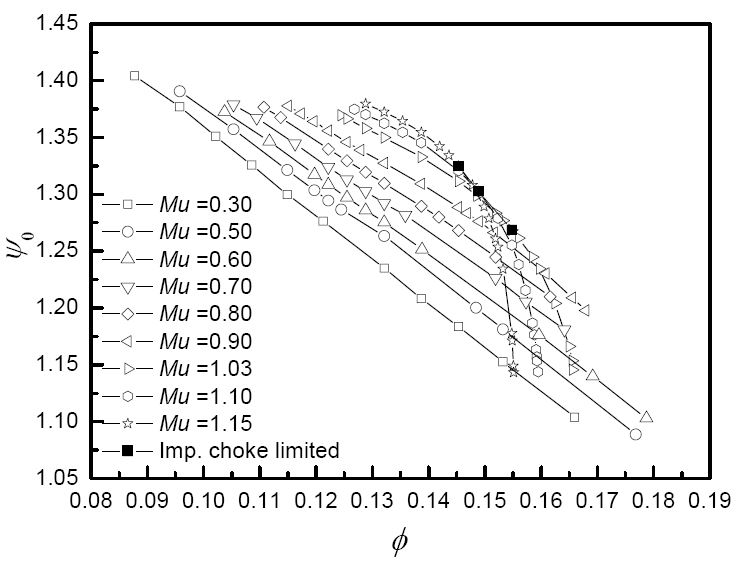
Fig. 5는 Euler’s pump equation과 관계된 일 계수(Work Coefficient)를 나타내었다. 임펠러 날개 회전속도 마하수가 일정할 경우 유량이 증가할수록 임펠러 출구에서의 반경방향 속도는 증가하고 회전방향 속도는 감소하기 때문에 일 계수는 이에 비례하여 감소한다. 또한 임펠러 날개 회전속도 마하수가 0.90부터 0.30으로 작아짐에 따라 단위 유량당 압축기 일이 비례하여 감소한다.

Fig. 6은 미끄럼 속도(Slip velocity)를 임펠러 날개 회전속도(Blade tip speed, U₂ )로 무차원화하여 나타내었고, 관련식은 식 (1)과 같다.

$\[ \frac{c_{\theta s}}{U_2}=1-\frac{c_{r2}}{U_2}\mathit{tan}{\beta }_2^{\text{'}}-\frac{c_{\theta 2}}{U_2}=1-{\varphi }_2\mathit{tan}{\beta }_2^{\text{'}}-\frac{{\psi }_0}{2} \]$

(1)

일정한 회전속도에서 유량계수가 증가할수록 무차원 미끄럼 속도는 작아지는데 이는 마찬가지로 임펠러 출구 반경방향 속도와 회전방향 속도의 변화로 임펠러 출구 와류비가 감소하기 때문이다. 또한 일정한 유량계수에서 임펠러 날개 회전속도 마하수가 증가할수록 반경방향 속도 증가 대비 회전방향 속도 증가율이 더 크기 때문에 무차원 미끄럼 속도 또한 증가하게 된다.

임펠러 입구부터 출구까지의 Polytropic 효율(η₁₂)을 Fig. 7에 나타내었다. 임펠러만의 효율로 봤을때 설계 유량계수에서 가장 높은 효율을 보이고 있으며, 일정한 유량계수에서 임펠러 날개 회전속도 마하수가 커질수록 효율이 높아지는 것을 확인하였다.

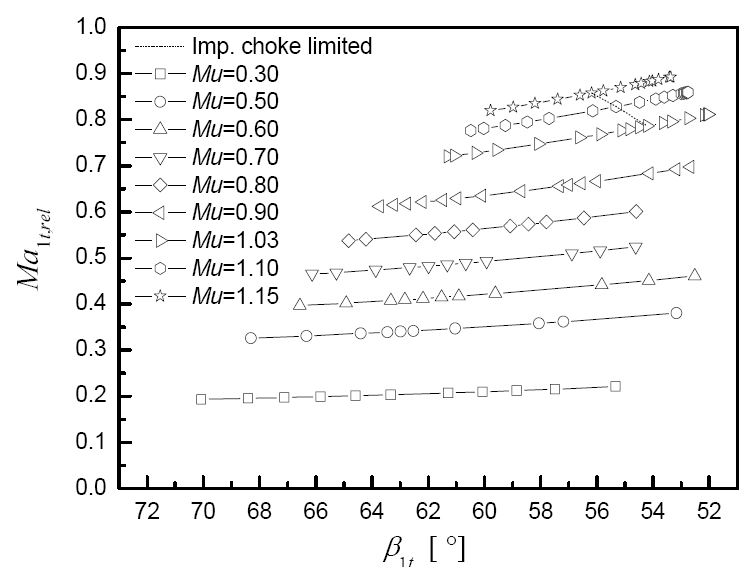
Fig. 8은 임펠러 유입 상대 유동각에 따라 임펠러 유입 상대 마하수를 나타내었다. 유량이 커질수록 축방향 속도와 유입 상대 속도가 커지기 때문에 입구 유입 상대 유동각은 작아지고, 유입 상대 마하수는 그에 비례하여 증가한다.

Fig. 5

Work coefficient for variations of flow coefficient and blade Mach number

Fig. 6

Variations of non-dimensional slip velocity

Fig. 7

Variations of polytropic efficiency of the impeller

Fig. 8

Variations of relative inlet Mach number and flow angle at the impeller tip (0.9span)

4.2.2 고 회전속도(M_u = 1.03∼1.15) 유동 특성

고 회전속도일 경우 낮은 유량에서는 저 회전속도에서와 같은 유동특성을 보이지만 유량을 증가시켜 임펠러 목에서 유량이 질식된 이후부터는 다른 특성을 보인다. Fig. 5에서 보듯 임펠러에서 질식이 진행된 이후로 일 계수가 급격하게 감소한다. 이는 임펠러 입구부 날개 끝(Shroud)에서 진행된 질식으로 인해 주 유동이 중심(Hub)을 통해 나가게 되어 반경방향, 원주방향 속도성분이 이전의 경향성과 달라지기 때문이다.

마찬가지로 질식이후 임펠러 출구 회전방향 속도 성분이 급격하게 작아지면서 무차원 미끄럼 속도는 저유량일 경우와 달리 급격하게 증가함을 알 수 있다(Fig. 6).

또한 Fig. 7에서 보듯이 임펠러 효율 약 0.94에서 동일하게 질식이 발생되며, 유량을 그보다 더 증가시킬 경우 날개 끝부터 발생한 유량질식이 중심으로 진행되면서 목영역 후단에서 발생하는 충격파에 의한 손실로 효율이 급격히 떨어지는 것을 관찰하였다.

Fig. 8에 나타난 바와 같이 유입되는 상대 유동각에 따라 상대 마하수가 다르기 때문에 유입 마하수가 작더라도 입사각이 큰 음의 수를 갖을 경우 임펠러 목에서 유량이 질식될 수 있음을 보여준다.

4.3. 디퓨저 내부 유동 특성

4.3.1 임펠러 초킹에 의한 영향

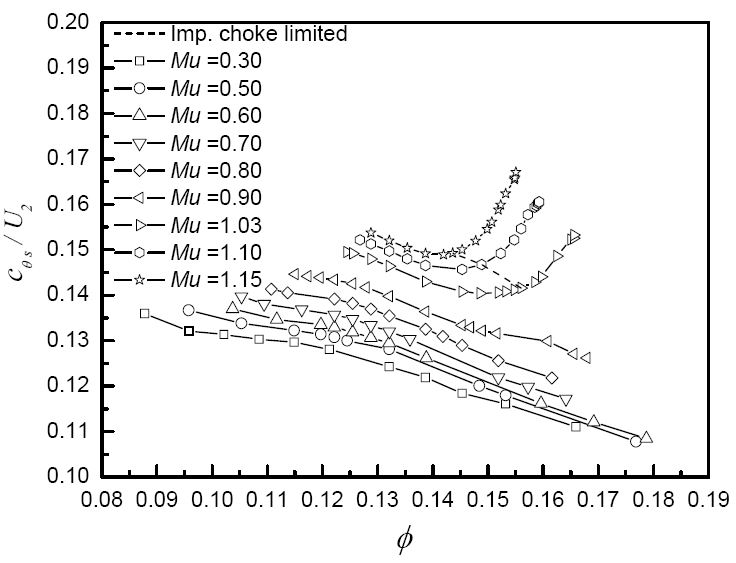
임펠러 출구를 나와 디퓨저로 들어가는 절대 유동각은 Fig. 9와 같다. 저 회전속도(M_u = 0.03∼0.90)에서 유량이 증가함에 따라 임펠러 출구 절대 유동각은 줄어들게 되는데 이는 유량이 증가할수록 임펠러 출구에서의 반경방향 속도는 증가하고 원주방향속도는 감소하기 때문이다. 특히 고 회전속도(M_u = 1.03∼1.15)에서 초킹 유량을 지나 유량계수를 늘릴 경우 임펠러 출구 유동각이 급격히 줄어드는 것을 볼 수 있는데 이는 날개 끝 부근에서 질식이 일어나면서 주 유동이 중앙(Hub)부근을 통해 나가게 되고 이에 따라 자오면(Meridional) 속도성분이 경향성과 다르게 더 커지고 반대로 원주방향 절대 속도성분은 더 급격하게 작아지기 때문이다. 고유량으로 갈수록 줄어든 임펠러 출구 유동각은 디퓨저 베인에 들어가는 유동각과 동일하게 간주할 수 있고, 따라서 유량을 증가시킬수록 디퓨져 베인 입사각은 0보다 많이 작은 상태로 유입하게 된다.

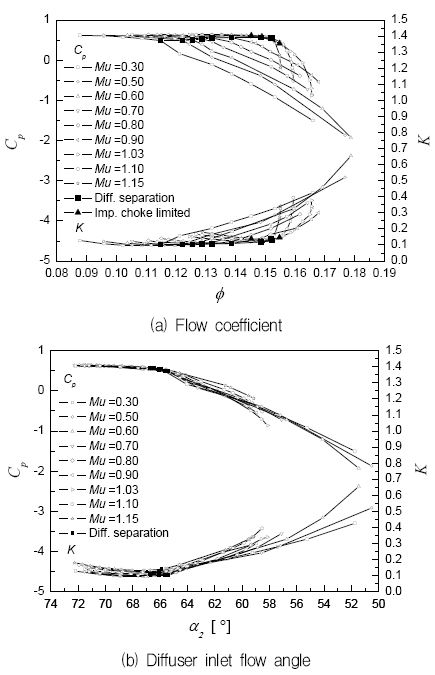
Fig. 10은 디퓨저를 통해 회복되는 정압량을 디퓨저 입구의 동압량으로 무차원화시킨 정압 회복 계수(Static pressure recovery coefficient)와 디퓨저를 거치며 손실한 전압량을 입구 동압량으로 무차원화한 손실 계수(Loss coefficient)를 나타내었다. Fig. 10 (a)를 보면 유량이 증가할수록 디퓨저 입출구의 정압비가 감소하기 때문에 정압회복계수 또한 감소한다. 특히 고유량으로 갈수록 유량의 질식이 진행됨에 따라 고 회전속도(M_u = 1.03∼1.15)에서의 압력회복계수는 급격하게 감소되는 것을 확인할 수 있다. 임펠러에서 유량이 질식되기 전까지의 일정한 유량계수에 대해서는 예상한바와 같이 회전속도가 증가할수록 정압회복계수 또한 증가한다.

손실계수의 경우 특정 입사각에서 최소값이 존재하며, 일정한 저유량계수에 대해서는 회전속도가 증가할수록 손실계수가 증가하고 반대로 임펠러 유량질식이 일어나기 전까지의 일정한 고유량계수에 대해서는 손실계수가 감소하는 것을 확인하였다. 고 회전속도에서 유량이 질식될 경우 충격파에 의한 손실이 디퓨저까지 이어져 손실계수는 급격히 상승하게 된다.

Fig. 9

Variations of inlet flow angle of diffuser

Fig. 10

Variations of static pressure recovery and loss coefficient of the diffuser

4.3.2 디퓨저 압력면 박리에 의한 영향

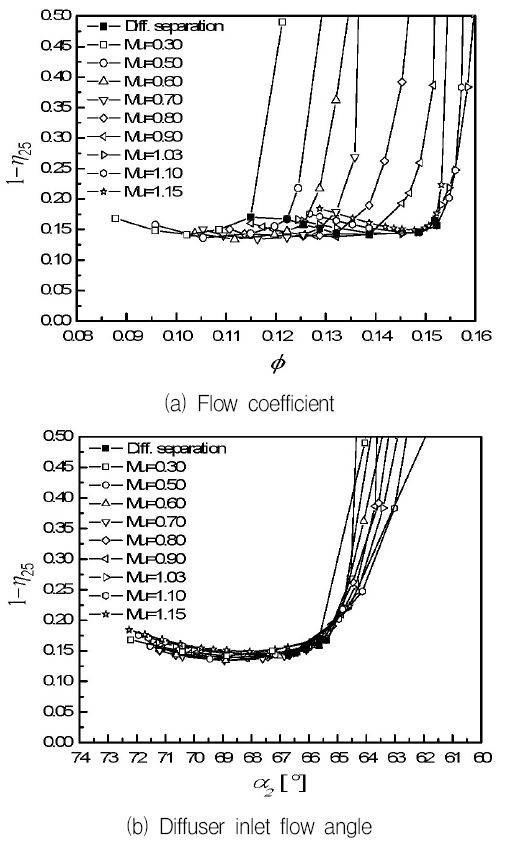
Fig. 10을 보면 유량이 증가하고 임펠러 출구 유동각이 감소하면서 회전속도와는 관계없이 출구 유동각 65.5도 부근에서 정압회복계수 약 0.5 이하로 급격한 감소를 보이며, 마찬가지로 임펠러 출구 유동각 65.5도 부근에서 급격한 손실을 보이고 있다. 이는 디퓨저 날개로 들어오는 입사각이 유량이 증가되면서 큰 음수값을 갖게 되고 이에 따라 날개 압력면에서 박리가 발생하기 때문에 얻은 손실로 볼 수 있다.

같은 관점으로 디퓨저 입구부터 출구까지 폴리트로픽 효율(η₂₅)을 Fig. 11에 나타내었다. 보는 바와 같이 박리가 발생하기 시작한 이후부터는 유량이 증가될 경우 디퓨저 베인 압력면에서의 박리에 의한 성능 저하로 효율이 급격하게 떨어진다. 또한 유동각이 약 65.5도 이하로 떨어질 경우 압력면에서의 박리로 인해 디퓨저 효율은 급격히 감소하게 된다. 이렇게 모든 회전속도에서 효율이 급격히 감소되는 원인으로는 디퓨저에서의 박리가 지배적이라는 것을 알 수 있다.

Fig. 11

Variations of polytropic efficiency of the diffuser

5. 결 론

산업용 원심 압축기의 공력 성능 및 유동 특성을 평가하기 위해 수치해석을 통한 결과를 분석하여 얻은 결론은 다음과 같다.

• 1) 원심 압축기 공력성능 특성을 분석하고 예측하기 위해 여러 임펠러 회전속도에 따른 가능한 전 유량에 대하여 수치해석 계산을 수행하였고 압축기의 각 요소 별로 확인하였다.
• 2) 임펠러는 저/고 회전속도로 그 특성을 나누어 초킹 발생 전후에 따른 성능과 손실특성을 분석하였고, 이는 계산이 수행되지 않은 회전속도 영역에 대해 선형적으로 예측될 것으로 판단된다.
• 3) 고 회전속도(M_u = 1.03∼1.15)로 작동되는 압축기에 유량을 늘릴 경우 임펠러 날개에 유입되는 마하수는 증가하고 입사각은 작아진다. 이에 따라 목에서의 날개 끝(Tip)부근에서 초킹이 발생하고 주 유동이 중앙(Hub)을 통해 흘러나가면서 임펠러 출구에서의 유동각이 급격하게 줄어들게 된다.
• 4) 디퓨저는 유입각이 약 65.5도 이하로 줄어들게 될 경우 베인 전단 압력면에서의 속도가 흡입면에서 보다 커지고 압력은 반대로 작아지게 되며 확산(Diffusion)을 겪어 유동 박리가 발생하게 된다. 베인 압력면에서의 박리 발생 전후에 따른 성능과 손실특성을 분석하였고, 이는 적절한 변수를 통해 예측할 수 있을 것으로 판단된다.

References

• Swain, E., (2005), “Improving a One-Dimensional Centrifugal Compressor Performance Prediction Method”, Proc. IMechE Part A, 219, p653-659. [https://doi.org/10.1243/095765005X31351]
• Aungier, R. H., (2000), Centrifugal Compressors-A Strategy for Aerodynamic Design and Analysis, ASME, New York.
• Oh, H. W., and Yoon, E. S., Chung, M. K., (1997), “An Optimum Set of Loss Models for Performance Prediction of Centrifugal Compressors”, Proc. IMechE Part A, 211, p331-338. [https://doi.org/10.1243/0957650971537231]
• Cumpsty, N. A., (1989), Compressor Aerodynamics, Longman Group, Pearson Education Ltd, Harlow, Essex, UK.
• Casey, M., and Robinson, C., (2013), “A Method to Estimate the Performance Map of a Centrifugal Compressor Stage”, Transactions of the ASME, Journal of Turbomachinery, 135.
• Japikse, D., (1996), Centrifugal Compressor Design and Performance, ETI,Inc, Wilder, Vermont, USA.