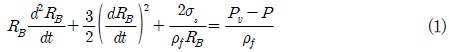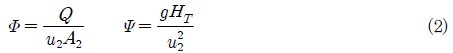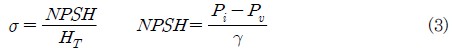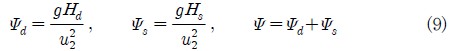Numerical Analysis on Cavitation of Centrifugal Pump

2.1. 펌프 실험장치 및 제원

Fig. 1

Layout of experimental apparatus

Table 1

Specification of centrifugal pump

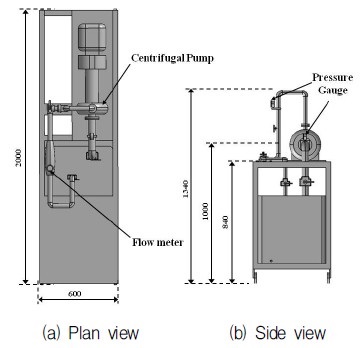
본 연구에서 상용프로그램의 수치해석 결과를 검증하기 위해 Gunt사의 원심펌프 성능실험장치(HM305)를 사용하였으며 Fig. 1은 실험장치의 (a)평면도와 (b)측면도를 나타낸다. 또한 본 성능실험 장치에 장착된 원심펌프는 Lowara사의 FHF32-125며 Table 1에 제원을 제시하였다.

2.2. 격자계

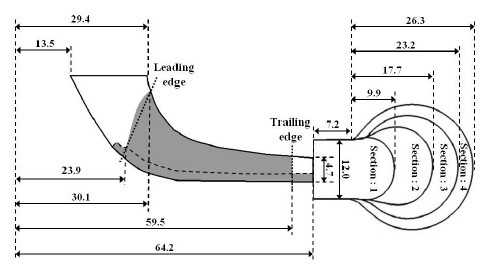
지금까지 수행된 많은 해석이 컴퓨터 용량 및 해석시간의 이유로 임펠러만을 대상으로 이루어졌다. 그러나 비 대칭인 스파이럴 케이싱(이하 케이싱)의 특성으로 인하여 이와 같은 방법으로는 정확한 해석이 불가능하다. 따라서 본 연구에서는 실제 현상에 대한 정확한 해석을 위해서 원심펌프의 완전한 형상을 3차원 스캔 장치인 COMET5-4M를 이용하여 구현하였다. Fig. 2는 수치해석에 사용된 임펠러와 케이싱의 형상을 보여주고 있다.

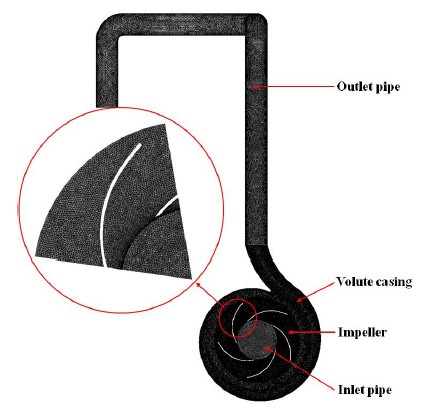
Fig. 3은 ANSYS ICEM CFD를 이용하여 생성된 전체 격자계이며 임펠러, 케이싱, 입구파이프와 출구 파이프로 구성되어있다. 실험 장치에서 입, 출구의 압력측정은 각각 입구로부터 230mm, 출구로부터 650mm에서 이루어진다. 따라서 수치해석에 있어서 경계조건의 정확성을 기하기 위해 실험장치와 동일조건의 입, 출구 조건을 주었다. 격자수는 임펠러와 케이싱이 2,800,000개와 1,200,000개 이며 임펠라 입구과 케이싱 출구에 연결된 입, 출구 파이프가 1,000,000개로 총 5,000,000개의 격자로 되어있고 사면체(tetrahedron)격자와 육면체(hexahedron)격자를 혼합하여 사용하였다. 또한 계산의 정확성을 위해 벽 근처에서 사용된 사면체격자에는 10개 이상의 프리즘(prism)격자를 설정하였고 이곳에서 y+의 값이 1이하가 되도록 제한조건을 두었다.

Fig. 2

Geometry and parameters of centrifugal pump

Fig. 3

Entire grid of computational domain

2.3. 수치해석

수치해석은 상용 프로그램인 ANSYS CFX 13을 사용하였다. 지배방정식은 단상류 해석인 경우 3차원 비압축성 Reynolds-Averaged Navier-Stokes 방정식이며 캐비테이션 해석인 경우 Rayleigh-Plesset model인 식(1)을 함께 사용하였다.

여기서 R_B, σ_s, ρ_f, P 와 P는 각각 기포의 반경, 표면장력계수, 액체의 밀도, 포화수증기압과 기포 주위에서의 액체의 압력을 의미한다. 실험에서 사용된 물의 평균온도가 25℃이므로 수치해석에서도 25℃의 물을 사용하였다. 경계조건은 입, 출구에서 각각 전압 및 질량 유량을 주었고 회전하는 임펠러와 정지된 케이싱의 접합부분에서는 과도 정익 동익(Transient Rotor Stator)기법을 사용하였다. 난류모델은 회전 유체기계에서 비교적 정확한 결과를 예측할 수 있는 SST모델을 사용하였다.

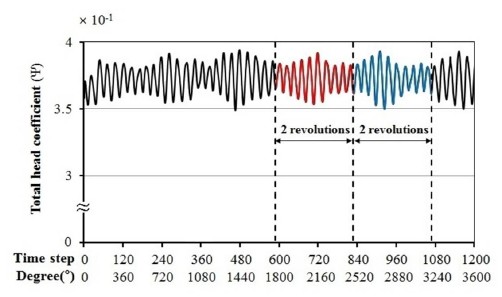
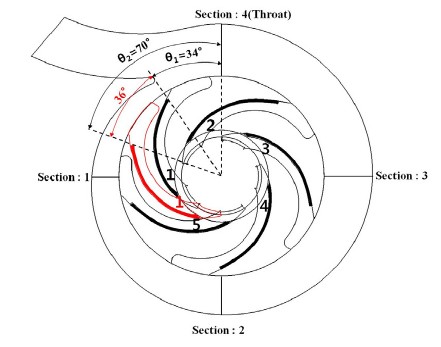
Fig. 4는 2.857×10^-4s(3°)의 시간간격(time step)으로 과도해석의 대표적인 결과를 보여주고 있다. 그림에서 36° 를 주기로 최대값과 최소값이 나타나며 2회전의 주기를 갖는데 이와 같은 현상은 임펠러의 날개가 회전하면서 혀의 영향을 받기 때문에 발생하게 된다.(7) 본 논문에서는 임펠러가 5회전 이후부터 2회전주기의 경향을 나타내고 있는데 이러한 경향을 바탕으로 한다면 5회전 이후 2회전의 평균이 과도해석의 해가 될 것이며 따라서 모든 수치해석의 결과는 이와 같은 방법으로 구하였다. Fig. 5는 목을 기준으로 임펠러 날개 끝부분의 각도를 나타냈으며 θ₁=34° 는 혀가 임펠러 날개의 끝부분과 일치할 때를 의미하고 θ₂=70° 는 임펠러 유로 가운데에 위치할 때를 의미한다. 앞서 언급한 상황을 종합적으로 고려하면 원심펌프의 정확한 해석을 위해서는 완전한 형상에서 과도해석방법이 전제 되어야한다.

Fig. 4

Solution of transient analysis

Fig. 5

Shape and blade positions of impeller

3.1. 성능곡선

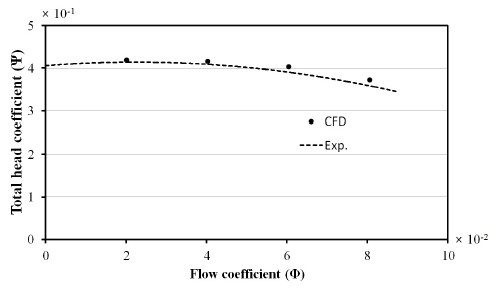
Fig. 6는 수치해석의 신뢰성을 확인하기 위해 펌프의 성능곡선에 대한 실험결과와 단상류의 수치해석 결과를 나타냈다. 그림에서 실험값은 5회 반복실험의 평균값이며 x축과 y축은 각각 유량계수(Φ)와 수두계수(Ψ)를 나타내며 식 (2)와 같다.

여기서 Q, H_T, u₂, A₂, g는 각각 유량과 전수두, 임펠라 출구의 주속도, 임펠러 출구의 통로면적과 중력가속도를 의미한다. Table 2에 유량에 따라 실험 및 수치해석의 수두계수 그리고 실험값을 기준으로 한 오차를 제시하였다. 유량에 따른 수두계수의 변화를 살펴보면 유량계수 Φ=2.02(×10^-2)를 기준으로 유량이 증가함에 따라 수치해석의 결과가 실험결과 보다 높게 나타난다. 이와 같은 오차는 임펠러와 케이싱 사이에서 발생하는 누설유량 및 기계적 손실을 수치해석에 반영하지 못한 데 기인한 것으로 유량이 증가함에 따라 미세하지만 증가한다. 하지만 모든 유량 범위에서 약 3% 이하의 오차를 나타내고 있기 때문에 수치해석의 결과에 대한 신뢰성을 가질 수 있다. 여기서 하첨자 CFD, Exp.은 각각 수치해석과 실험을 의미한다.

Fig. 6

Performance curves of experimental and numerical analysis

Table 2

Error of performance curves according to flow coefficient

3.2. 캐비테이션

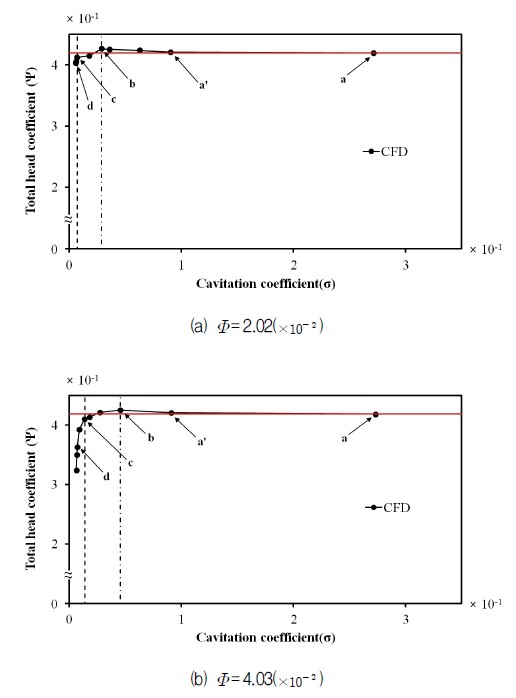
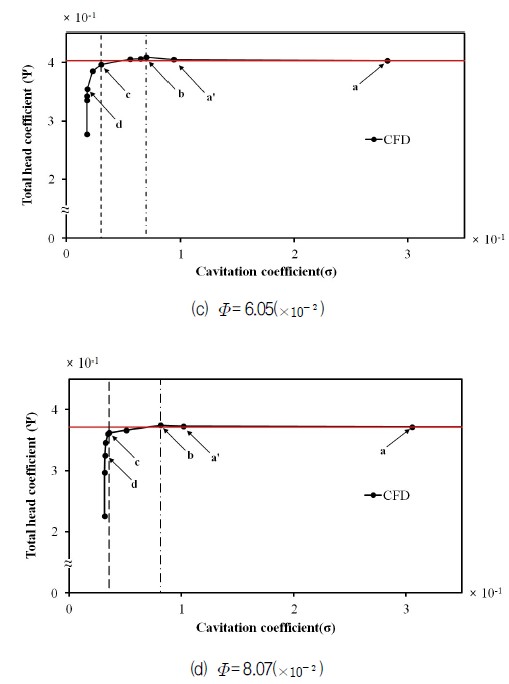
Fig. 7은 이상류 해석에서 흡입조건의 변화(캐비테이션 계수 변화)에 대한 수두변화를 각 유량계수에 따라 나타내었다. 그림에서 x축은 Thoma의 캐비테이션계수(σ)로서 식 (3)과 같다.(4)

여기서 P_i와 γ는 각각 흡입구의 전압, 비중량을 의미한다. 그림에서 일점쇄선은 이상류 해석에서 캐비테이션에 의한 수두감소 현상을 감지할 수 있는 가장 높은 수두 b의 캐비테이션 계수이며 점선은 급격한 수두 감소가 시작되어 캐비테이션이 완전 확립으로 추정되는 캐비테이션 계수 c를 나타내며 x축에 수평한 붉은 선은 캐비테이션의 영향을 받지 않는 위치에서의 평균 수두를 의미한다. 그림에서 캐비테이션 계수가 감소함에 따라 수두는 거의 일정한 붉은 선의 값을 유지하다가 일점쇄선 근처 a′에 이르면 증기가 조금 발생하게 되며 조금 더 감소하여 일점쇄선에 이르게 되면 수두는 약간 증가하여 b가 되며 캐비테이션 계수가 일점쇄선 보다 더 감소하면 점선의 수두 c까지 감소한다. 이러한 현상은 전 유량범위에서 공통적으로 나타나고 있으며 Fig. 7은 이러한 과정을 잘 보여주고 있다.

Fig. 7

Suction performance for the variation of the flow coefficient

Table 3

Head and cavitation coefficients and rate of change according to flow coefficient

Table 3은 Fig. 7에서 각 유량의 a, b, c, d점들을 수치화하여 제시한 표이다. 표에서 하첨자 red, b, c는 각각 a의 붉은선, b, c점을 가르친다. Fig. 3의 성능곡선은 우향 하강곡선이다. 그러므로 유량이 증가하면 수두는 당연히 감소하며 a(붉은선), b, c의 수두도 동반 감소하나 b, c의 캐비테이션 계수는 증가한다. 이 또한 식(3)에 의하면 당연한 결과라 하겠다. 여기서 b, c는 캐비테이션 발생 및 확립을 결정하는 중요한 점들이다. 이들의 거동을 살펴보면 붉은 선의 수두 a를 기준으로 유량에 따르는 b점의 수두 증가폭은 적은 유량에서는 크게, 큰 유량에서 적게 증가하여 유량이 증가하면 증가폭은 감소하지만 모든 유량에서 약 2% 이내(1.7%∼0.8%)이며 b점의 수두를 기준으로 점선인 c점의 수두는 모든 유량에서 거의 일정하게 약 3%(3.2%∼3.3%) 감소한다. 캐비테이션의 발생과정은 수두가 약간 상승한 후에 이를 기점으로 약 3% 감소한 다음 급격히 감소한다고 알려져 있다.(1) 위의 c점은 이러한 현상을 확인해 주고 있다. 또한 일점쇄선과 점선 사이의 거리인 캐비테이션 계수의 변화량은 유량이 증가함에 따라 커지는 것을 확인할 수 있다.

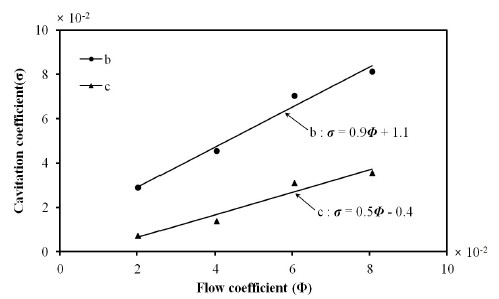
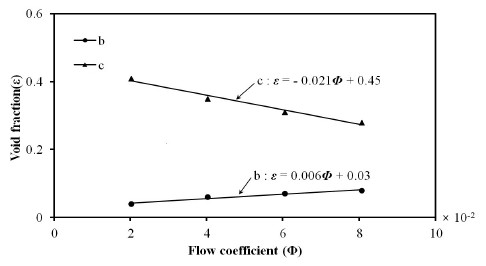
Fig. 8은 유량에 따라 캐비테이션 발생(b) 및 확립(c)의 캐비테이션 계수들의 변화를 보여주고 있다. 그림에서 유량이 증가하면 각 계수들은 증가하며 증가 속도는 캐비테이션의 발생이 확립보다 크게 나타난다. 이들을 1차식으로 제시하면 식(4)와 (5) 같이 표현된다.

Fig. 8

Cavitation coefficient of b and c according to flow coefficient

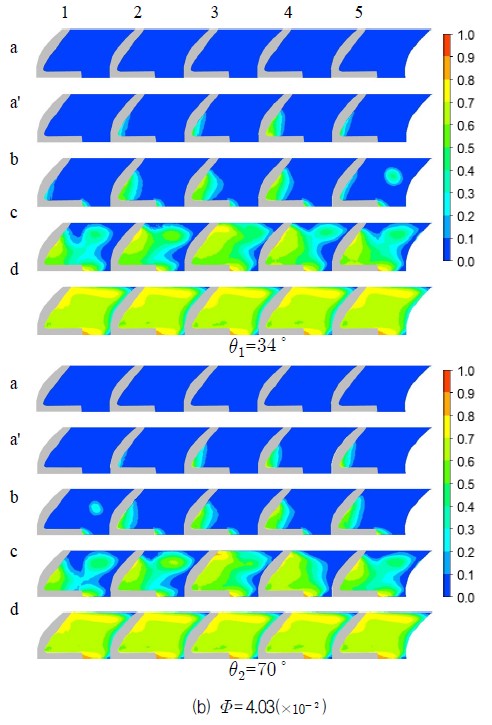
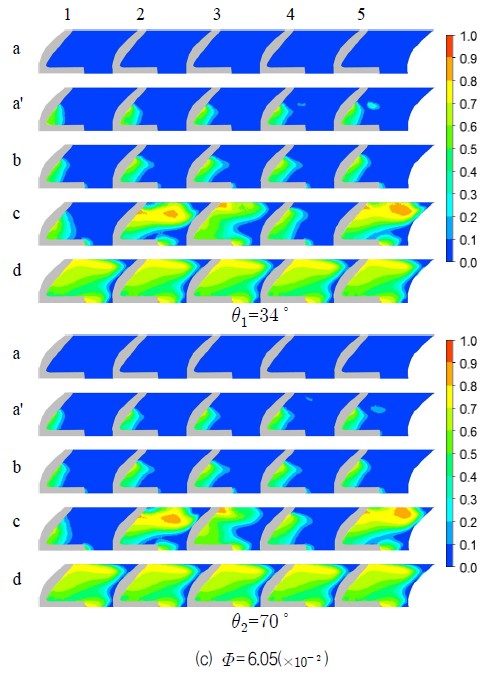
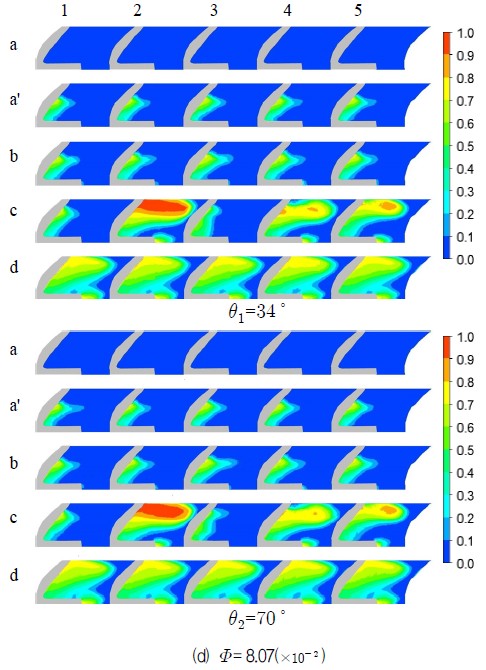
캐비테이션의 발생 및 성장 과정을 알아보기 위해 Fig. 2에 표시된 임펠라 깃 전연 단면에서 유량에 따라 식(6)과 같이 정의되는 기공율( )에 대한 분포도를 Fig. 9에 제시하였다.

여기서 A_g와 A_l은 각각 증기의 면적과 물의 면적을 나타낸다. 그림에서 각도(θ₁ = 34°, θ₂ = 70°)와 가로에 표시된 숫자(1, 2, 3, 4, 5)는 각각 임펠러의 회전 위치와 원주방향으로 임펠러 깃 전연의 계산단면을 의미하며 Fig. 2와 Fig. 5에 제시되어 있다. 세로에 표시된 문자(a, a′, b, c, d)는 Fig. 7의 a, a′, b, c, d를 나타내며 a, a′는 수두의 변화가 발생하지 않는 점 b, c, d는 각각 최고 수두점, 3%의 수두 감소점 그리고 급격한 수두감소를 나타나는 점들이다.

그림의 a′, b, c에서 캐비테이션은 모든 깃의 전연 부근 부압면에서 발생하며 깃 입구의 원주방향 위치에 따라 각기 다르게 성장한다. 이러한 현상을 캐비테이션의 발생과정과 연계하여 살펴보면 a′는 통상적으로 단상류에서 증발 시작점이라 할 수 있으며 b는 증기의 응집현상으로 유로가 약간 축소되어 속도에너지의 증가로 전수두가 약간 높아지게 되는 현상이 나타나는 것으로 볼 수 있는데 Table 3(1.7%∼0.8%)에서도 확인할 수 있다. 여기서 b는 통상적으로 캐비테이션의 확립에 따르는 수두 감소의 기준으로 고려되는 점이다. c는 b를 기준으로 약 3%의 수두감소가 발생하는 점으로 캐비테이션이 확립된 단계이며 원주방향으로 불규칙하지만 깃 전연 전영역이 증기의 영향을 받고 있으며 d는 더욱 더 그러하다. Fig. 9에서 θ₁ = 34°, θ₂ = 70°는 앞서 설명했듯이 케이싱 목을 기준으로 임펠러의 회전각도를 나타낸다. 각 유량에서 임펠라에 회전에 따른 깃 전연 단면의 기공율 분포는 a′, b ,c, d 모두 조금씩 다르다. 따라서 캐비테이션의 발생, 성장, 확립 전 과정에서 미세하지만 케이싱의 영향을 확인할 수 있다.

Fig. 9

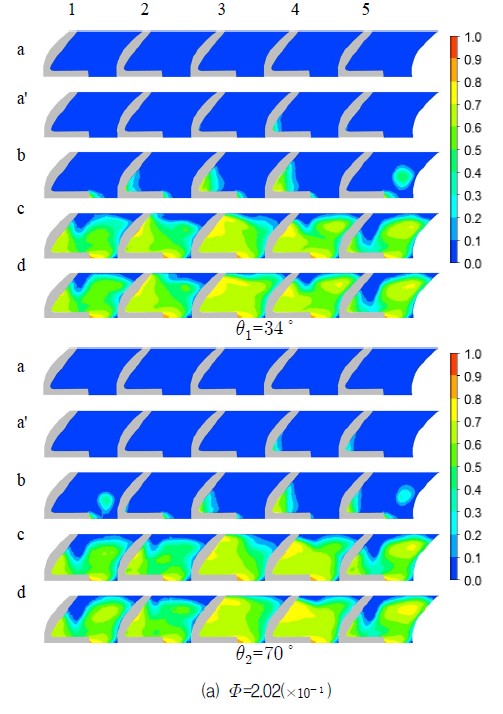
Void fraction distribution according to circumferential position & cavitation coefficient around blade-inlet of impeller

Table 4

Void fraction according to cavitation coefficient on leading line of blade

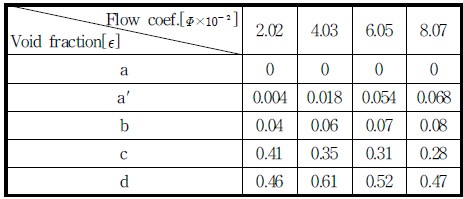
Table 4는 Fig. 9에 제시된 임펠라 깃의 전연에서 깃의 위치가 θ₁ = 34°와 θ₂ = 70°일 때의 기공율을 평균하고 다시 5개 익에서 평균하여 정량적으로 나타냈다. 기공율을 캐비테이션의 발생으로부터 완전확립에 이르는 a, a′, b, c, d에서 살펴보면 a에서는 단상류를 나타내는 것으로 유량에 관계없이 기공율이 0이며 a′에서는 같은 캐비테이션 계수 σ=1 부근(Fig. 7)에서 유량이 증가할수록 기공율이 커지는 것으로 보아 유량이 증가할수록 캐비테이션 발생을 나타내는 b의 캐비테이션 계수가 커지는 경향을 중간 단계에서 확인할 수 있다. 캐비테이션 발생을 감지할 수 있는 최고 수두를 나타내는 b는 a에 비해 증가하며 3%의 수두 감소로 캐비테이션 확립을 알리는 c점은 b점과 비교하면 큰 폭으로 감소함을 알 수 있다. d점은 c점의 수두에 약 10%정도 감소하는 위치로 완전 확립 단계를 나타내는데 c점에 비해 더 큰 기공율을 보이고 있다. 여기서 유량 Φ=2.02(×10^-2)의 기공율 0.46는 유량 대비 기기기기로 보면 다소 적은 값인데 그 이유는 극 저유량에서 수치해석이 불가능하여 b점 수두 대비 약 5%(10% 아님) 감소 지점의 값이기 때문이다. 여기서 기공율은 유량 증가에 따라 b점은 증가하지만 c, d는 감소한다. 유량증가에 따르는 캐비테이션 발생(b), 확립(c)의 기공율의 경향을 Fig. 10에 제시하였고 이들을 식으로 표현하면 각각 식(7), 식(8)과 같다.

Fig. 10

Void fraction of b and c according to flow coefficient

Fig. 11

Void fraction according to flow passage between blades

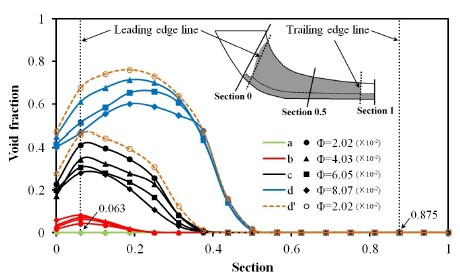
Fig. 11은 Table 4의 전연에서 각 유량의 a, b, c, d 점의 기공율을 기준으로 이 기공율이 유로를 따라 변화하는 과정을 제시하였다. 여기서 제시된 값들도 역시 회전각도와 5개 익의 평균값이다. 그림에서 x축은 익의 원주방향의 단면을 나타내며 0은 깃의 전연이 아니라 깃 입구 직전이고 1은 깃이 아닌 임펠라 출구를 의미한다. y축은 기공율이고 y축과 나란한 점선은 전연과 후연을 의미한다. 그림에서 보면 전연에서 각 유량의 캐비테이션 성장과정을 나타내는 a, b, c, d들의 기공율은 깃 입구 직전인 단면 0에서는 b를 제외하고 유량에 관계없이 거의 같은 값에서 시작되어 전연을 통과하면서 a, b, c, d는 각 유량에 따라 각각 다르게 성장하나 기공율이 사라지는 위치는 a, b, c, d 각각은 다시 유량에 관계없이 각각 한 점으로 모아진다. 캐비테이션 발생과 확립인 b, c점들의 최고 기공율을 나타내는 단면 위치은 모두 전연이며 사라지는 위치는 각각 0.25, 0.38이다. 한편 c점에서 d점으로 향한다는 의미는 기공율이 확립 보다 더 큰 완전 확립 상태로 진행한다는 의미하며 이 경우 기공율의 최고점은 깃 내부로 이동한다. 이와 같은 현상을 좀 더 시각적으로 보기 위해 유량 Φ=2.02(×10^-2)의 캐비테이션 확립인 c점에서 수두 대비5% 감쇠선와 또 완전 확립을 나타내는 수두 대비 10% 감쇄선을 빈 원으로 표시된 2개의 주황색 점선으로 표시하였다. 여기서 10% 감쇄선은 가상선이다. 이것을 보면 캐비테이션이 확립(c)에서 완전확립(d)로 변해가는 동안 기공율이 유로에 따라 변화하는 과정을 관찰할 수 있다.

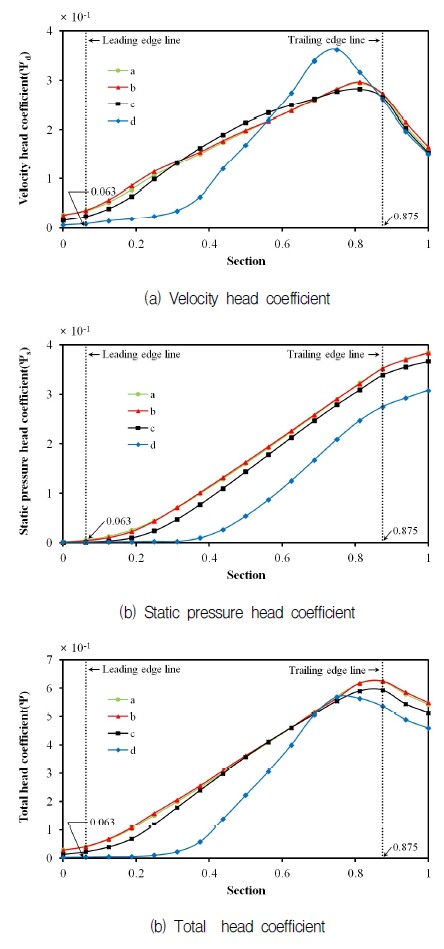
a, b, c, d들의 기공율들의 영향으로 동압, 정압, 전압이 깃 내부의 유로에 따라 변화하는 과정을 관찰하기 위해 유량 Φ=4.03(×10^-2)에서 다음 식과 같이 정의되는 이들의 계수들을 Fig. 12(a),(b),(c)에 제시하였다.

여기서 하첨자 _{d, s}는 각각 동압과 정압을 나타낸다. 모든 수두 계수에서 b는 캐비테이션 발생으로 a 보다 유로가 약간 좁아지므로 미미하지만 a의 수두 보다 약간 큰 값을 유지하면서 같은 경향으로 변화한다. 한편 c와 d는 캐비테이션 확립, 완전확립이다. 확립 c는 a, b보다 현저히 기공율이 높지 않기 때문에 a, b를 조금 벗어나 a, b를 따르나 완전확립인 d는 a, b, c와는 다른 양상이다. 원심펌프의 깃 내 유동은 증속류로 속도와 압력 모두 증가한다. 그림의 속도수두 Fig. 12(a), 압력수두 Fig. 12(b)도 이러한 경향을 잘 보여주고 있다. 속도수두인 Fig. 12(a)에서 b는 a보다 조금 큰 값을 유지한다. 이것은 앞서 설명하였듯이 캐비테이션의 발생이 유로를 축소하는 효과 때문이고 후연부터 임펠라 출구까지 속도수두가 감소하는데 이 부분에서는 깃이 없으므로 당연한 결과라 하겠다. 그리고 d는 캐비테이션 영향 때문에 깃의 35%까지 증가가 완만하다가 캐비테이션이 사라지면서 급격히 속도수두가 증가하게 된다. 이 또한 후연 전 약 75% 부근에서 고점을 기록한 후 감소한다. 그리고 깃 출구부터 임펠라 출구까지 b의 수두가 다른 수두보다 약간 높으면서 모두 거의 같은 값으로 모아진다. 정압수두를 나타내는 Fig. 12(b)에서는 a, b, c, d의 캐비테이션 기공율의 깃 내 분포도 때문에 a, b, c, d의 정압수두 증가 시작점은 서로 다르지만 같은 형상을 임펠라 출구까지 그대로 유지하며 역시 후연을 깃점으로 상승률이 둔화된다. 정압수두는 d를 제외하면 모두 거의 같은 경향이고 속도수두는 모두 일정한 차를 유지하면서 같은 경향을 나타낸다. 이들 두 수두의 합인 전압수두 Fig. 12(c)는 예상대로 d가 가장 큰 기공율 때문에 가장 낮은 전압 수두를 보이며 a, b는 앞서 설명대로 b가 a보다 약간 크게 나타난다. 이상을 종합하면 캐비테이션 발생 즉 b가 캐비테이션 발달과정 중 가장 높은 수두가 나타나며 어떤 경우라도 b를 초과할 수 없음을 확인 할 수 있었다.

Fig. 12

Head coefficients distribution according to flow passage between blades at Φ= 4.03(×10-2 )