Spiral Casing of a Volute Centrifugal Pump

1. 서 론

오늘날 에너지는 인간생활의 풍요로움, 산업에 기초한 국가 경쟁력 나아가 인류생존에 까지 큰 영향을 미치고 있다. 따라서 모든 분야에서 에너지의 효율적인 사용은 매우 중요한 문제라 하겠다.

원심펌프는 기계적 에너지를 작동유체에 전달하는 에너지 변환 장치로서 장치산업 및 플랜트산업 등 산업 전반에 걸쳐 사용되는 기본 장치이며 우리 일상에서도 널리 이용되고 있다. 기본 장치로서 광범위하게 사용되는 원심펌프의 성능향상은 막대한 에너지 사용이라는 측면에서 에너지의 효율적인 절약에 크게 기여할 것이다.

원심펌프는 축, 임펠러 그리고 스파이럴 케이싱(이하 케이싱)으로 구성되어 있다. 지금까지 많은 연구들이 구성요소의 핵심인 임펠러에 집중되어 왔다. 반면에 유체 유출 통로인 케이싱에 대한 연구는 상대적으로 소홀히 되었으나 원심펌프의 진일보된 성능향상이라는 측면에서는 케이싱 내 유동에 직접적인 영향을 주는 케이싱 형상에 대한 연구가 반드시 뒷받침되어야 한다.

지금까지 케이싱에 대한 연구를 살펴보면 Van den Braembussche는 케이싱 내부유동의 손실 메커니즘 및 케이싱의 성능평가를 위한 파라미터를 제시하였다.(1) Marc Gugau는 과도(transient)기법을 사용하여 임펠러와 스파이럴 케이싱 경계면에서 반경방향, 원주방향 속도 및 정압분포를 분석하였으며(2) 임펠러와 스파이럴 케이싱 경계면에서 유동현상에 관한 연구도 있다.(3^~5) Kim과 Baek은 스파이럴 케이싱의 입구 높이가 성능변화에 미치는 영향에 대해 연구하였으며(6) Yang and Kong은 스파이럴 케이싱 목의 넓이가 효율에 미치는 영향을 조사하였고(7)스파이럴 케이싱 표면 거칠기가 성능에 미치는 연구(8) 등도 있다. 스파이럴 케이싱의 단면모양에 대한 연구로는 Mishina와 Gyobu에 의한 원형, 정사각형, 직사각형 단면에서 전 수두의 손실에 대해 연구하였고(9) Ayder는 직사각형 보다 타원형이 더 효율적이며(10) Lee와 Choi는 사각단면에서의 손실 메커니즘으로 임펠러 출구에서 허브와 쉬라우드에서의 속도 차이로 코너 부분에 2차유동의 발생에 대한 연구를 수행하였다.(11)

본 연구에서는 스파이럴 케이싱의 단면형상변화가 성능곡선에 미치는 영향을 조사하기 위해 산업현장에서 사용되는 원심펌프를 모델로 수치해석을 수행하여 스파이럴 케이싱의 특성을 파악하였다.

2. 수치해석

2.1. 모델과 격자

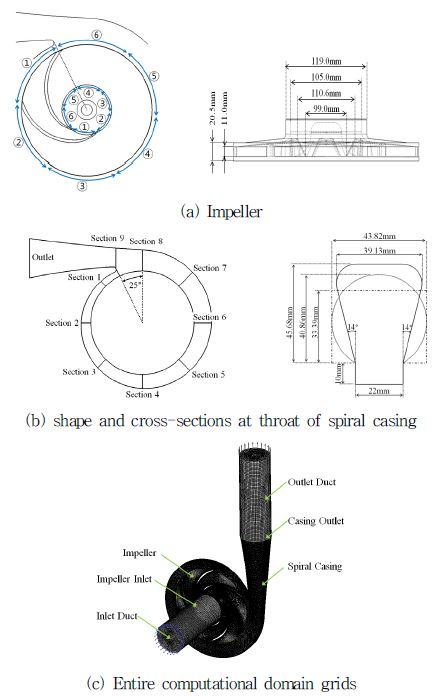
본 연구에 사용된 계산모델은 산업현장에서 사용되고 있는 단단 스파이럴 볼류트 원심펌프로서 임펠라는 6개의 깃으로 구성되어 있으며 Fig. 1은 구성요소인 임페라 및 케이싱 그리고 전모델(full model)의 계산격자의 개략도이다. 설계조건은 회전속도 1750rpm, 유량 66m³/h, 수두 32m이다. 계산시간의 불리함에도 불구하고 완전한 형상의 원심펌프를 모델로 선택한 이유는 스파이럴 케이싱의 비대칭으로 임펠러 내부의 각 깃에 형성되는 상이한 유동장이 케이싱 유동에 다시 영향을 주는 현상을 정확히 파악하기 위해서다.

Fig. 1

Geometry and grid of centrifugal pump

Fig. 2

Comparison between the performance curves of experimental and numerical analysis

Table 1

Total head comparison for experimental and numerical analysis

임펠러 및 스파이럴 케이싱에 있어서 형상구현은 각각 ANSYS Blade Editor 및 캐드(CAD)를 사용하였고 각각의 격자는 ANSYS Turbo-Grid로 육면체(Hexahedron) 격자를 그리고 ANSYS ICEM-CFD로 사면체(Tetrahedron) 격자를 생성하였다. 그 결과 임펠러 깃은 한 개당 200,000개, 스파이럴 케이싱 2,500,000개 그리고 실험조건과 유사한 입, 출구의 파이프에서 각각 150,000개의 격자가 사용되어 총 4,000,000개의 격자가 사용되었다. 또한 수치해석의 정확도를 높이기 위하여 모든 벽면으로부터 10개 층의 격자에서 y+를 1 이하로 설정하였다.

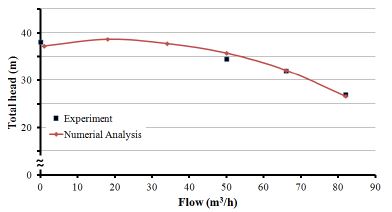
본 연구에 사용되는 수치해석의 신뢰도를 확인하기 위하여 수치해석 결과를 제작사에서 제시한 실험값과 비교하여 Fig. 2와 Table 1에 나타내었다. 표에서 최대오차가 3.5% 미만이므로 수치해석 결과를 신뢰할 수 있는 수준으로 평가하였다.

Fig. 1(b)의 오른쪽 그림은 스파이럴 케이싱 단면형상의 변화에 대한 개략도이며 목에서 단면 모양이 다른 세 가지 경우를 제시하고 있다. 기본모델인 기준모델은 사다리꼴의 단면형태이며 다른 두 가지 모델은 기준모델의 단면적과 케이싱 높이가 같으면서 모양을 원형 및 사각형으로 변화시킨 형태이다.

2.2. 수치해석 방법

수치해석은 ANSYS CFX 13을 사용하여 수행하였다. 경계조건은 입구에 대기압, 출구에 질량유량을 주었으며 계산유량은 성능곡선의 전 영역을 6가지(0m³/h, 18m³/h, 34m³/h, 50m³/h, 66m³/h, 82m³/h)로 변화시켰다. 이 때 성능곡선의 수두계산은 파이프의 입, 출구가 아니고 임펠러 입구, 스파이럴 케이싱 출구에서 이루어졌다. 작동유체는 물을 사용하였으며 난류모델은 벽면의 유동박리에 비교적 정확한 SST(Shear Stress Transport)를 사용하였다. 실제 임펠러가 회전하면서 내부 유동이 변화과정을 관찰하기 위해 임펠러와 스파이럴 케이싱 경계면에 Transient Rotor Stator기법을 적용하였다. 이 때 시간간격(time step)은 2.857×10^-4이고 총 계산시간은 0.3425s이며 각각 임펠러가 3˚ 회전시간 및 10 회전 시간을 의미한다. 또한 수렴조건으로 나머지(residual)값을 1×10^-4 그리고 최대 반복계산 횟수를 100회로 설정하였다. 이렇게 설정한 이유는 1×10^-5 및 100회 이상으로부터 얻어진 결과와 차이가 없었기 때문이다.

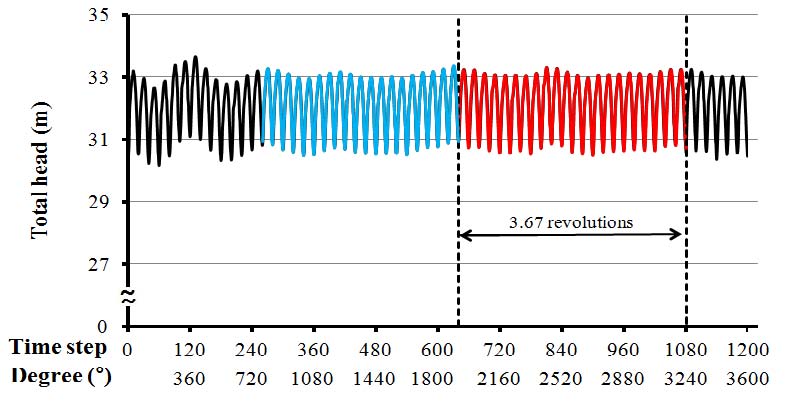
Fig. 3는 기준모델의 설계유량에서 Transient Rotor Stator 기법을 이용하여 수치해석을 수행하였을 때 임펠러의 10회전 동안 수두의 변화를 보여준다. 그림에서 60˚를 주기로 최대, 최소값이 나타나며 어느 정도 회전 후 파란색과 빨간색 같이 유사한 패턴이 나타난다. 앞으로 제시되는 특별히 언급하지 않는 값들은 측정패턴을 검토하여 반복패턴이 확인된 후의 한 개 패턴을 평균한 값들이다. 여기서 60˚ 주기로 수두가 완전히 동일하지 않는 이유는 다음에 설명하기로 한다.

Fig. 3

The solution of transient analysis

3. 결과 및 토의

Fig. 2는 일반적인 원심펌프의 성능곡선으로 체절점으로 부터 우향 상승 및 하강곡선의 형태를 가진다. 스파이럴 케이싱은 임펠러에서 나온 유체가 외부로 방출되는 통로로서 이곳에서 발생하는 에너지 손실은 성능곡선에 큰 영향을 미친다. 따라서 스파이럴 케이싱의 형상은 펌프성능에 매우 중요한 요소이며 이러한 형상은 단면 크기 및 모양으로 대변될 수 있겠다. 본 연구에서는 단면 형상이 성능에 미치는 영향을 조사하고자 한다.

Fig. 4

Total head curves according to cross-sectional shapes

Table 2

Total head difference for 3 models

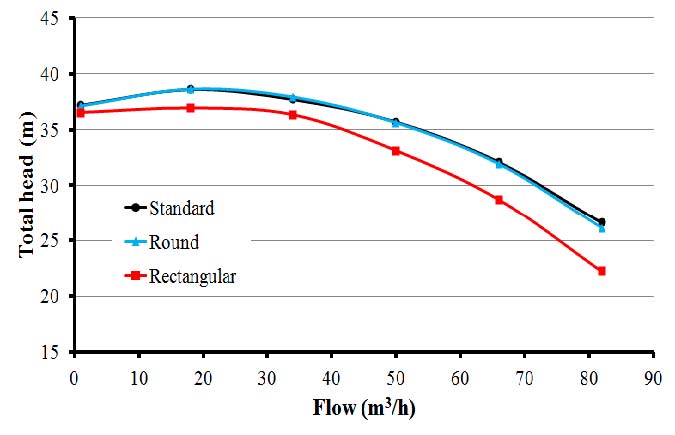
Fig. 4는 케이싱 단면형상에 따른 성능곡선 형태를 보여주고 있으며 Table 2에 그 편차율을 수치화하여 제시하였다.

그림에서 기준모델은 앞서 언급 하였듯이 우향 상승 및 하강곡선의 형태를 보이며 원형 모델도 이와 유사하다. 이는 Table 2에서도 확인할 수 있다. 한편 사각형 모델의 수두는 기준모델보다 낮으며 유량이 증가할수록 그 차가 커지며 곡선의 형태는 우향 하강을 보여준다. 결과적으로 기준모델과 원형모델은 차이가 없으며 사각형모델과는 분명한 차이를 보이고 있다.

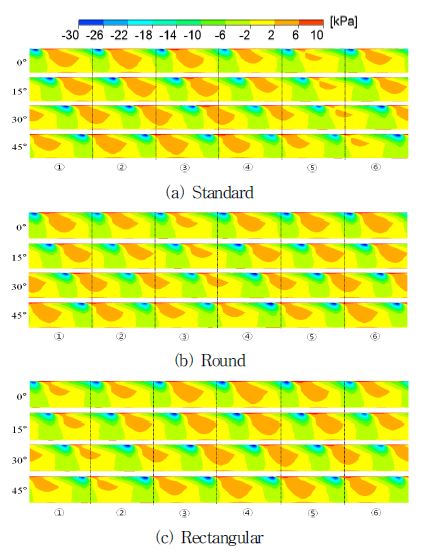
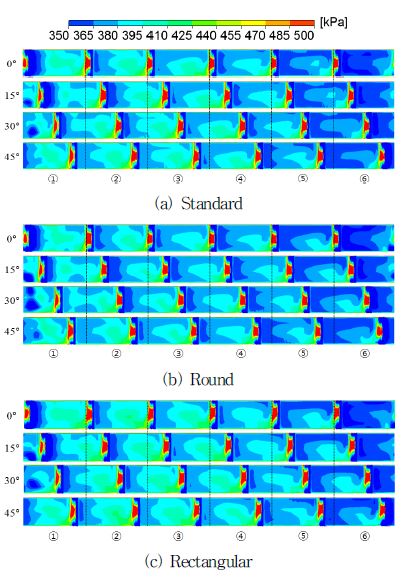
성능곡선의 특성에 차이가 없는 기준 모델 및 원형모델 그리고 뚜렷한 차이를 보이는 기준(혹은 원형)모델과 사각형 모델에 대하여 스파이럴 케이싱의 비대칭성이 역으로 깃 입구 직전 및 깃 출구 직후 즉, 깃의 직접적 영향이 없는 영역의 유동장에 미치는 영향을 알아보기 위해 설계유량(66m³/h)에서 이곳들의 전압분포를 Fig. 1(a)의 왼쪽 그림에 표시된 깃의 순서에 따라 Fig. 5(a),(b),(c) 및 Fig. 6(a),(b),(c)에 각각 제시하였다. 그림에서 가로의 ①∼⑥는 Fig. 1(a)의 깃의 순서이고 세로의 숫자는 깃의 한 피치 구간에서 15˚ 씩 회전을 의미하며 그림에서 0˚는 임펠러 깃이 section8과 맞닿는 경우를 나타낸다. 깃 입구 직전의 전연부분인 Fig. 5에서 기준모델은 (a), 원형모델은 (b), 사각형모델은 (c)이다. 세 모델 모두 깃의 회전에도 불구하고 깃 입구에서 전압분포의 모양은 비슷하지만 크기는 같지 않다. Fig. 5(a)의 0˚에서 보면 ⑤영역에서 제일 높은 값이 다른 영역의 제일 높은 값보다 분포면적이 현저히 적으며 다른 영역에서도 모양은 비슷하지만 분포의 크기는 서로 동일하지 않다. 이러한 분포형태는 깃의 회전에 따라 같이 회전한다. 그리고 이와 같은 현상은 모델에 관계없이 동일하게 나타난다. Fig. 5에서 세 모델은 한 피치 60˚ 구간만 보여주고 있지만 이러한 현상은 깃이 360˚ 즉, 1회전에 걸쳐 일어난다. 이것은 모델에 관계없이 케이싱의 비대칭성이 깃 입구 영역에 영향을 주고 있음을 확인할 수 있다. 한편 깃 출구 직 후 유동장인 Fig. 6에서는 깃의 위치에 따르는 분포의 유사성은 찾아볼 수 없고 또 입구처럼 회전에 따르는 분포의 회전도 혀 근처의 복잡한 유동으로 인하여 찾아볼 수 없으며 각 모델간의 유사성도 또한 찾을 수 없다. 출구에서 이와 같은 현상은 당연한 결과라 하겠다. 따라서 깃의 회전에 의한 출구의 전압 변화가 Fig. 3과 같이 나타나는 것은 당연한 결과라 하겠다.

Fig. 5

Total pressure distribution just before blade inlet

Fig. 6

Total pressure distribution just after impeller outlet

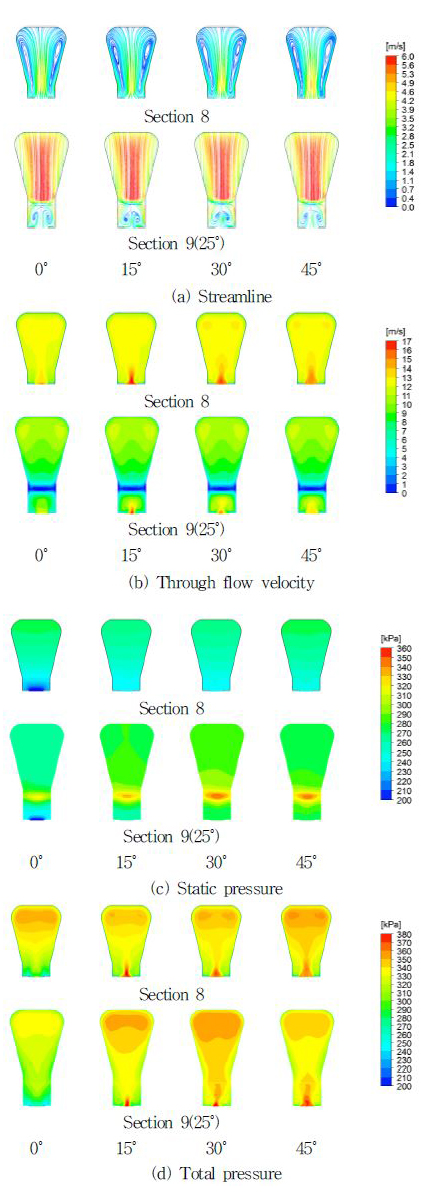
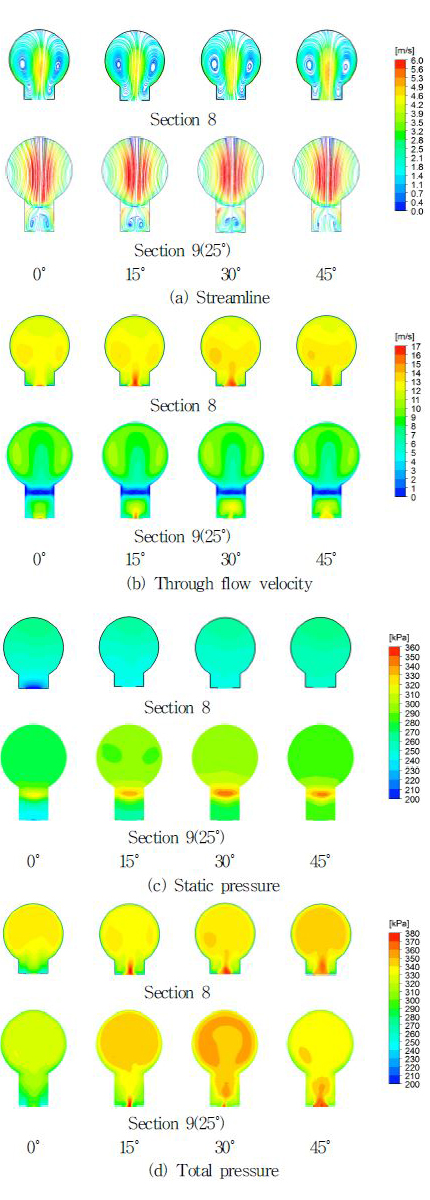
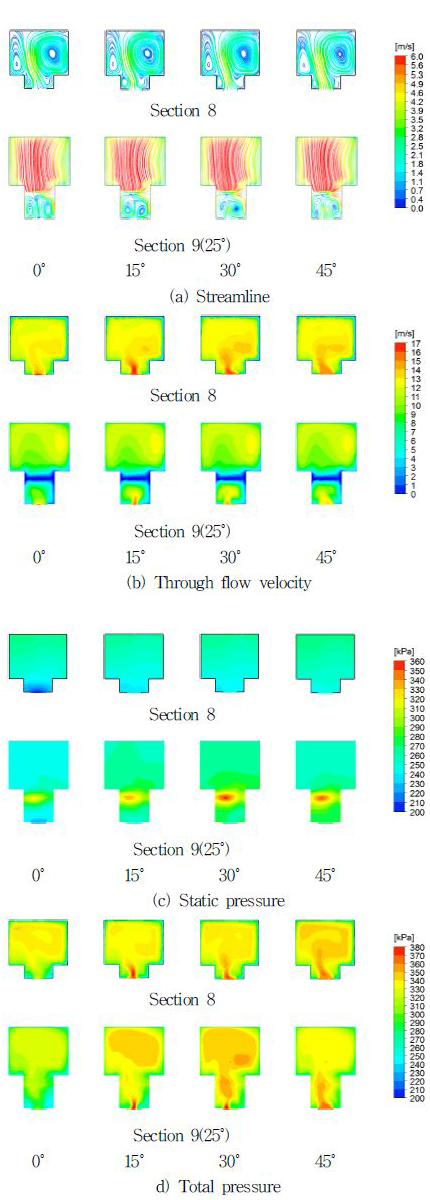
모델 형상은 앞서 언급하였듯이 수두곡선에 영향을 미친다. 그 영향을 포괄적으로 알아보기 위해 설계유량(66m³/h)에서 그리고 Fig. 1(b) 왼쪽 그림에 제시된 케이싱의 목과 혀를 지나는 단면인 section8과 section9에서 반경방향유선, 주유동속도, 정압, 전압들을 케이싱 단면의 형상에 따라 Fig. 7(표준모델), Fig. 8(원형모델), Fig. 9(사각모델)에 나타내었다.

Fig. 7, Fig. 8, Fig. 9(이하 각 그림)에서 Fig. 7(a), Fig. 8(a), Fig. 9(a)인 반경방향의 유동을 나타내는 유선은 케이싱 중심으로 유입된 유체는 케이싱 외주 벽 에 부딪힌 후 내벽을 따라 선회운동을 하면서 2개의 강제와류를 형성한다. 그 형태가 기준모델과 원형 모델은 깃의 위치에 관계없이 대칭이며 일정한 형태를 가지나 사각형 모델은 비대칭이고 일정하지도 않다. 그리고 section9는 혀를 지나는 두 개의 단면으로 위쪽은 케이싱 출구가 시작하는 단면인데 이곳에서 유선은 와류 없는 직선을 나타내며 아래쪽은 케이싱의 시작 단면으로서 모든 그림에서 2개의 와류가 나타나는데 여기서도 기준모델과 원형 모델은 대칭이며 사각형 모델은 비대칭이다.

각 그림에서 Fig. 7(b), Fig. 8(b), Fig. 9(b)인 원주방향의 주유동(through flow) 속도분포를 살펴보면 목인 section8이 임펠러 깃과 맞닿을 때(0˚, 60˚)에는 임펠러 깃과 일치하므로 케이싱 입구 부근에서 약한 속도분포가 형성되지만 30˚는 깃 출구의 한 피치 구간의 중간이기 때문에 30˚까지 강해지다 다시 약해진다. 이런 현상은 모든 모델에서 나타난다. 스파이럴 케이싱 내부에서는 기준모델 및 원형 모델은 거의 대칭이며 사각형 모델은 비대칭유동이 나타난다. 한편 Section9에서 스파이럴 케이싱 시작 단면인 아래 단면에서는 전 모델이 Section8과 같은 현상을 나타내고 section9의 위 단면인 케이싱 출구 시작 단면에서는 기준모델과 원형모델은 깃의 회전각도와 관계없이 대칭이며 사각형 모델은 회전각도에 따라 비대칭이다

각 그림에서 Fig. 7(c), Fig. 8(c), Fig. 9(c)인 정압분포는 앞서 설명한 이유로 section8에서 깃과 목이 일치할 때는 케이싱 입구에 낮은 정압이 형성되었다가 임펠러 회전에 따라 회복된다. 이외 나머지 부분에서는 모든 모델에서 임펠러 회전에 관계없이 거의 균일한 분포를 가진다. Section9에서는 혀로 인한 유동의 정체로 그곳에서 높은 정압분포를 나타내며 section9의 나머지 단면에서는 모든 모델이 깃의 각 회전각도에서 대칭으로 나타난다.

각 그림에서 Fig. 7(d), Fig. 8(d), Fig. 9(d)인 전압 수두분포는 주유동 속도분포와 유사하다. 이것은 정압수두분포가 거의 균일하므로 전압수두분포는 주유동 속도분포에 영향을 받는 것으로 당연한 결과라 하겠다. 따라서 주유동이 전압 형성에 많은 영향을 미친 것으로 볼 수 있다. 여기서 자주 언급되는 케이싱 내의 비대칭 유동장은 대칭 유동장 보다 손실이 크다는 사실이 이미 선행 연구(1)(9)에서 언급된 바 있고 이에 대한 메카니즘도 소개되었다.(11)

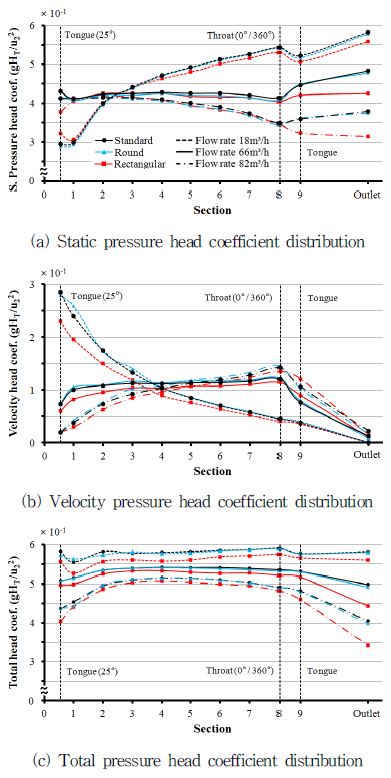
Fig. 10은 Fig. 1(b)의 왼쪽 그림에서 스파이럴 케이싱의 혀로부터 목을 지나 출구까지 각 단면에서 정압수두, 속도수두 및 전압수두 분포들을 나타내고 있다.

Fig. 7

Internal flow at volute of standard model

Fig. 8

Internal flow at volute of round model

정압수두분포인 Fig. 10(a)에서 section1∼section8에서는 설계유량일 경우 세 모델이 거의 균일하나 저유량에서는 증가하고 고유량에서는 감소한다. 이러한 경향은 케이싱의 적정 단면적 보다 큰 경우 유속이 느려지면서 압력이 증가하는 반면 그 반대의 경우 유속이 빨라지면서 압력이 감소하는 현상을 반영한 것이다. 그리고 목에서 혀까지인 section8∼section9에서는 설계유량 고유량에서는 증가하고 저유량에서는 감소한다. 그런데 사각형 모델은 다른 두 모델의 경향을 설계유량, 고유량에서는 따라가지 못하고 벗어난다. 그리고 압력회복을 기대하는 확대관인 section9에서 출구까지는 정압이 상승하나 사각형 모델은 앞서 언급한 경향들이 더욱 두드러지게 나타난다. 따라서 사각형 모델은 목과 혀 사이 뿐 만 아니라 출구 확대관에서 정압 회복에 적합하지 않은 형상을 의미하며 이러한 원인은 유동의 비대칭성에 있다고 하겠다.

Fig. 9

Internal flow at volute of rectangular model

Fig. 10

Head distributions according to spiral casing

속도수두분포인 Fig. 10(b)의 section1∼section8에서 설계유량에서는 압력수두분포와 같이 거의 균일하나 저유량, 고유량에서는 압력수두분포와 반대 경향을 보이고 있으며 특히 저유량일 때 혀 부근에서 사각형모델이 다른 모델보다 낮게 분포되어 있다. 하지만 목인 section8에서는 모델별로 모아지고 출구까지 모델별로 기울기는 다소 다르지만 감소하여 거의 하나의 값으로 모아진다.

전압은 정압과 동압의 결합으로 표현된다. 전압수두 분포인 Fig. 10(c)에서 스파이럴 케이싱을 나타내는 section1∼section8에서는 설계유량을 중심으로 고유량과 저유량에서는 정압과 동압이 서로 반대 경향이므로 그 결합은 일정한 값을 유지하리라 예상할 수 있다. 예상대로 기준모델과 원형 모델은 유량에 따라 거의 동일하고 고유하게 일정한 값을 가지며 사각형 모델은 각 유량에 따라 위 두 모델과 일정한 차를 유지하며 비슷한 경향을 가진다. 다만 고유량으로 갈수록 케이싱 혀와 목에서 휘어 활과 같은 모양을 보이고 있다. 그리고 목과 혀 사이인 section8∼section9에서는 설계유량에서 세 모델 모두 거의 일정하나 나머지 유량에서는 감소하는 것으로 보아 전체적으로 감소하는 경향이라 말할 수 있다. 또 혀와 출구사이에서는 저유량일 경우 모든 모델에서 일정하나 고유량으로 갈수록 감소폭이 커져 출구 확대관에서 전압상승효과는 고유량일수록 기대하기 어려우며 사각형 모델일 경우 더욱 그러하다.

이상을 종합하면 케이싱 출구에서 동압은 모든 모델 모든 유량에서 아주 적은 하나의 값으로 수렴하므로 케이싱 출구 전압은 출구 확대관의 정압 회복에 의해 지배된다. 그림에서 유량이 증가할수록 각 모델의 전압상승 능력은 감소하고 특히 사각형모델의 경우 감소 경향이 더욱 뚜렷해진다.

4. 결 론

스파이럴 케이싱의 단면 형상의 변화가 성능곡선에 미치는 영향은 다음과 같다.

1) 성능곡선에 있어서 기존모델과 원형모델은 거의 차이가 없이 동일한 형태를 나타내고 있으나 사각형모델은 기존모델보다 큰 차이의 적은 값으로 그리고 우향 하강의 특성을 나타난다. 이의 원인은 비대칭 유동장에 있다.

2) 스파이럴 케이싱 비 대칭성은 케이싱 모델에 관계없이 임펠라 입구유동에 영향을 준다.

3) 케이싱 내에서 정압수두분포는 모델에 관계없이 유량별로 거의 같은 유형을 갖고 있으면서 설계유량에서는 일정, 저유량에서는 증가, 고유량에서는 감소 경향을 갖는다. 그리나 확대관인 목에서 출구까지는 같은 유량에서도 대칭 혹은 비대칭 유동장의 모델에 따라 다른 경향을 가진다.

4) 동압수두분포는 케이싱 그리고 목에서 출구까지 유량에 따라 모델에 관계없이 거의 같은 형태를 가지며 경향은 케이싱 내에서 정압수두분포와 반대로 나타나고 목에서 출구까지는 감소하여 한 점으로 모아진다.

5) 전압분포는 케이싱에서는 정압수두분포와 동압수두분포의 조합으로 거의 일정하게 나타나며 목에서 출구까지는 정압수두분포의 영향으로 고유량 사각형모델일수록 크게 감소한다.

6) 이상을 종합하면 비대칭 유동장을 유발하는 모델은 에너지 효율성이라는 측면에서 적합지 않다.

Acknowledgments

본 연구는 2012년도 울산대학교 기계공학부 일류화사업단의 연구비에 의해 수행되었으며 이에 감사드립니다.

References

• R.A. Van den Braembussche, “Flow and Loss Mechanisms in Volutes of Centrifugal Pumps”, Design and Analysis of High Speed Pumps, (2006), p12-1-12-26.
• Marc Gugau, “Transient Impeller-volute Interaction in a Centrifugal Pump”, Interer Bericht, Turbomachinen TU Darmstadt, (2003.).
• G. Pavesi, “Impeller Volute and Diffuser Interaction”, Design and Analysis of High Speed Pumps, RTO-ENAVT-143, (2006), p6-1-6-28.
• Cheah. Lee, Winoto, “Unsteady Analysis of Impeller-Volute Interaction in Centrifugal Pump”, International Journal of Fluid Machinery and Systems, (2011, July-September), 4(3), p349-359. [https://doi.org/10.5293/IJFMS.2011.4.3.349]
• Cheah. Lee, Winoto, “Numerical Study of Inlet and Impeller Flow Structures in Centrifugal Pump at Design and Off-design Points”, International Journal of Fluid Machinery and Systems, (2011), 4(1), p25-32. [https://doi.org/10.5293/IJFMS.2011.4.1.025]
• S. Kim, J. Park, K. Ahn, J. Baek, “Improvement of the Performance of a Centrifugal Compressor by Modifying the Volute Inlet”, Journal of Fluids Engineering, (2010), 132, ASME, p091101.1-091101.7. [https://doi.org/10.1115/1.4001972]
• Sunsheng Yang, Fanyu Kong, Bin Chen, “Research on Pump Volute Design Method Using CFD”, International journal of Rotating Machinery, (2011), 2011, Article ID 137860, p1-7. [https://doi.org/10.1155/2011/137860]
• 강신형, 홍순삼, “볼류트의 개선에 따른 원심펌프의 성능향상”, 대한기계학회 춘계학술대회논문집 B, (1997), p570-575.
• Mishina, I., Gyobu, “Performance Investigations of Large Capacity Centrifugal Compressor”, ASME paper NO. 78-GT-3, (1978.).
• Ayder, E., “Experimental and Theoretical Analysis of the Flow in a Centrifugal Compressor Volute”, Transactions of the ASME, Journal of Turbomachinery, (1993), 115, p582-589. [https://doi.org/10.1115/1.2929293]
• 이기수, 최창호, 김진한, 양수석, “임펠러/벌류트의 상호작용을 이용한 원심펌프의 성능예측”, 한국전산유체 공학회 학술대회 논문집, (2001), p203-207.